解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
ポイントは、中心の動きを元にして円の回転数を考えることです。
では、この流れに沿って解いていきましょう!
円の回転数は何で決まる?
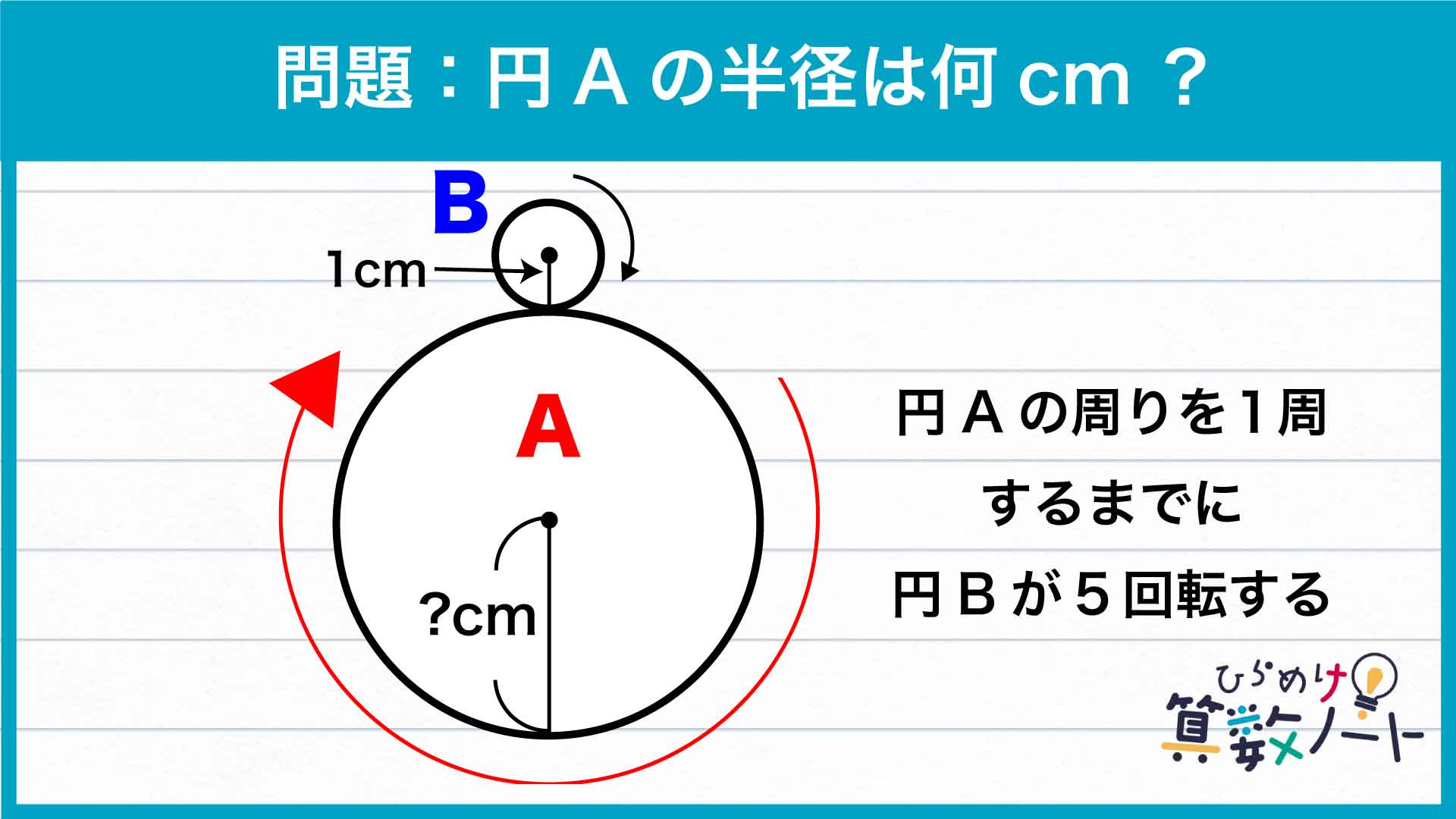
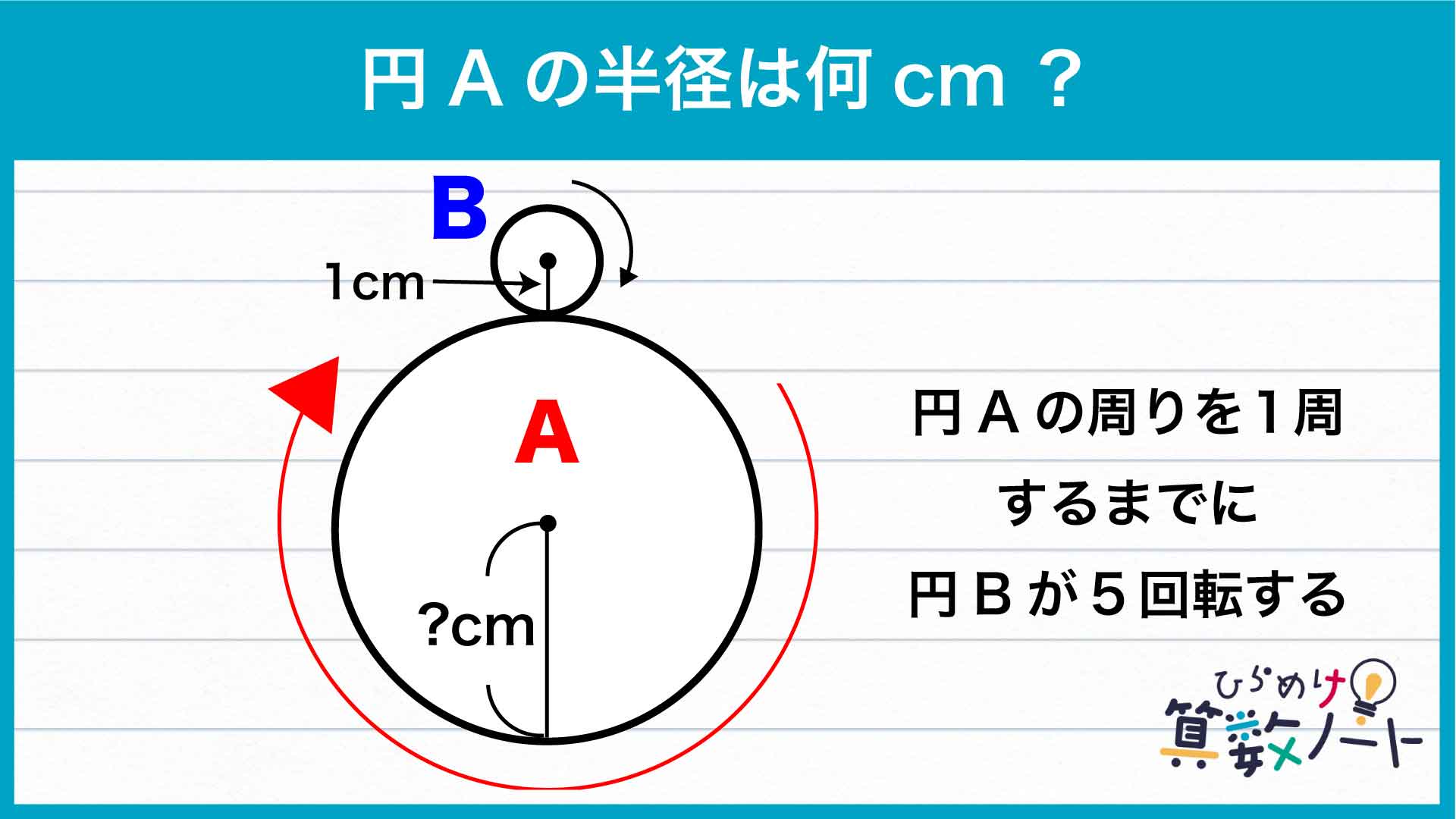
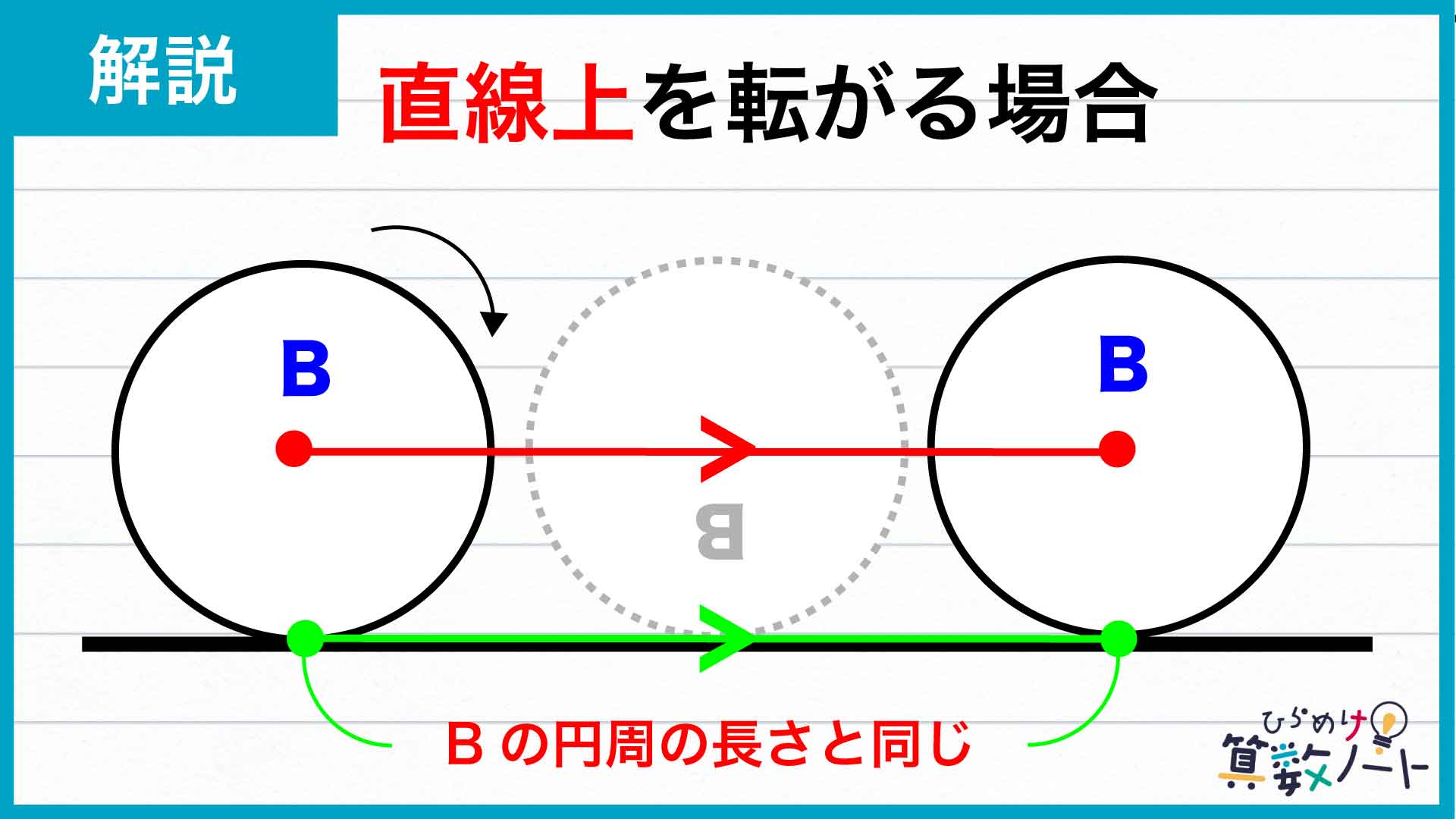
この問題、「円Bは円周と同じ長さをなぞるたびに1回転するはず」と考え、「5cm」と答えてしまった人も多いのではないでしょうか。確かに、下図のように直線の上を転がる場合は、円Bが円周と同じ長さ(図の緑線部分)をなぞったときにちょうど1回転しています。
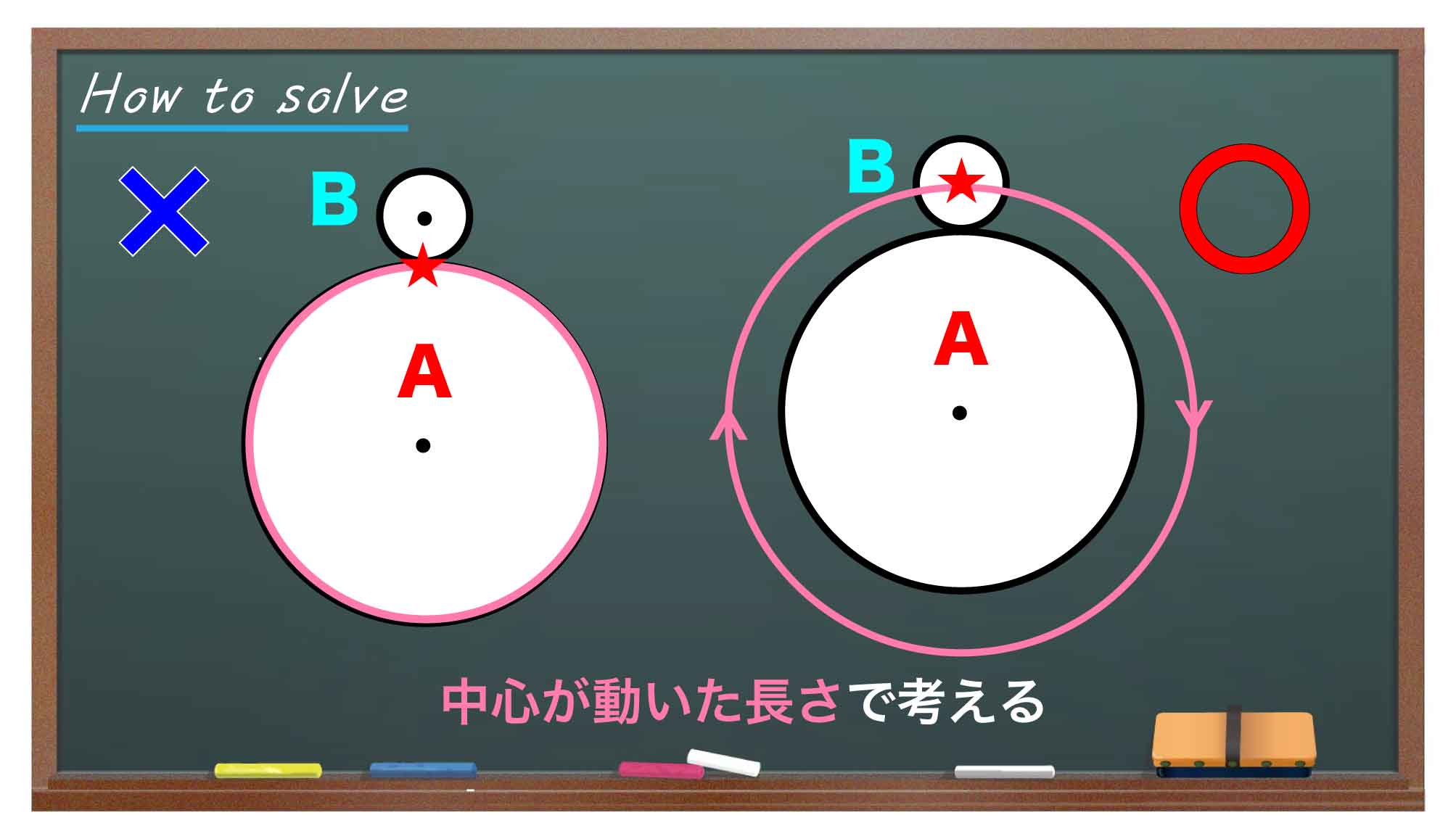
ただしこのとき、円Bの中心もまた円周と同じ長さ(図の赤線部分)だけ動いています。実は、円Bの回転数を決めるのはこの「中心が動いた長さ」なのです。
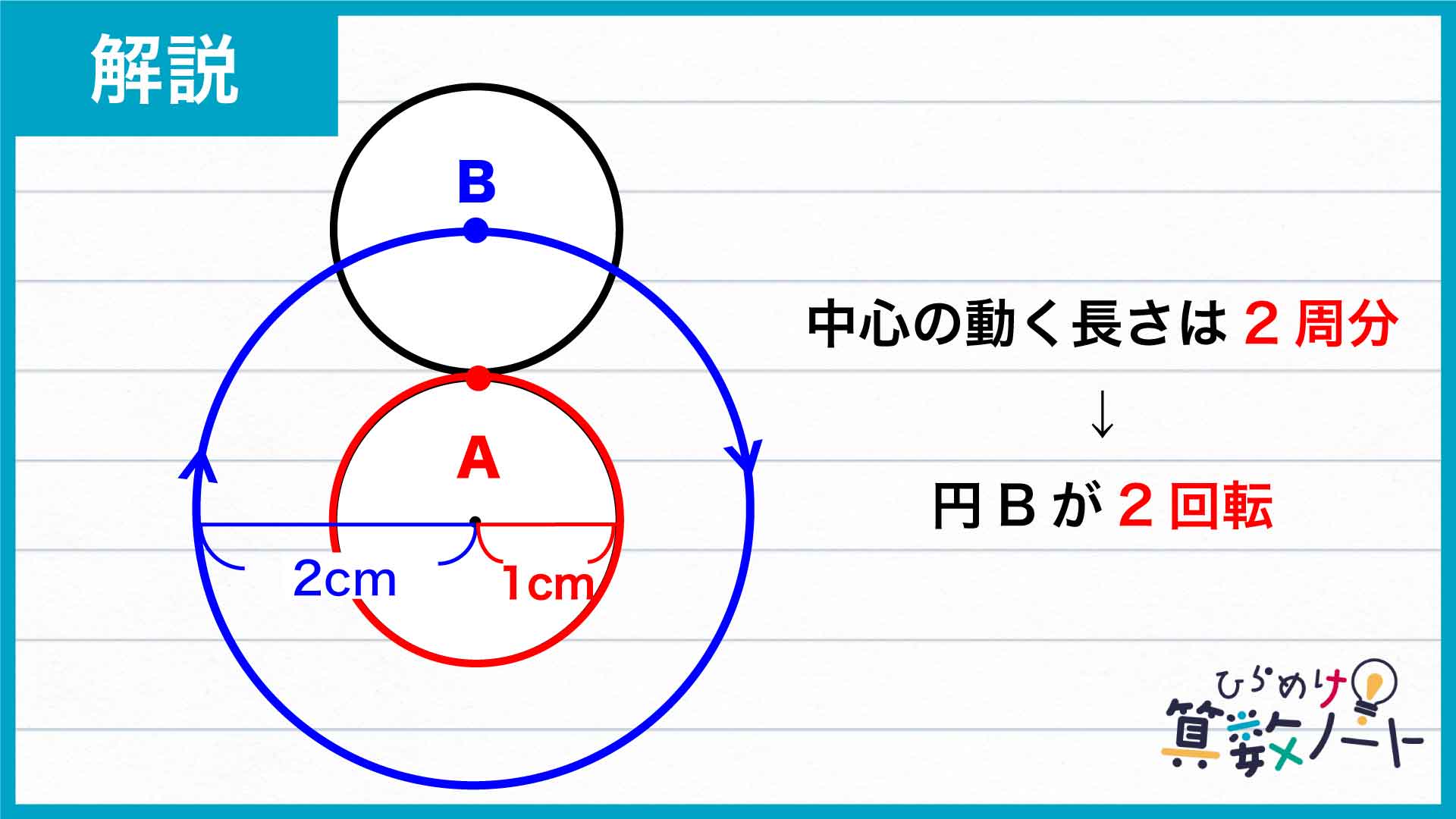
2ページ目のヒントでは、「円Aと円Bの半径が共に1cmのとき、円Bは円Aの周りを1周する間に2回転する」という例を紹介しました。こちらも、円Bがなぞった長さ自体は直線上を転がる場合と同じです。しかし、中心の動きを追ってみると、その軌跡は半径2cmの円になっているとわかります。
円周の長さは半径×2×円周率で求められるので、半径が2倍になれば円周の長さも2倍になります。つまりこの場合、中心がBの円周と比較して倍の長さを動いているので、円Bは円Aの周りを1周する間に2回転したのです。
中心の軌跡を考える
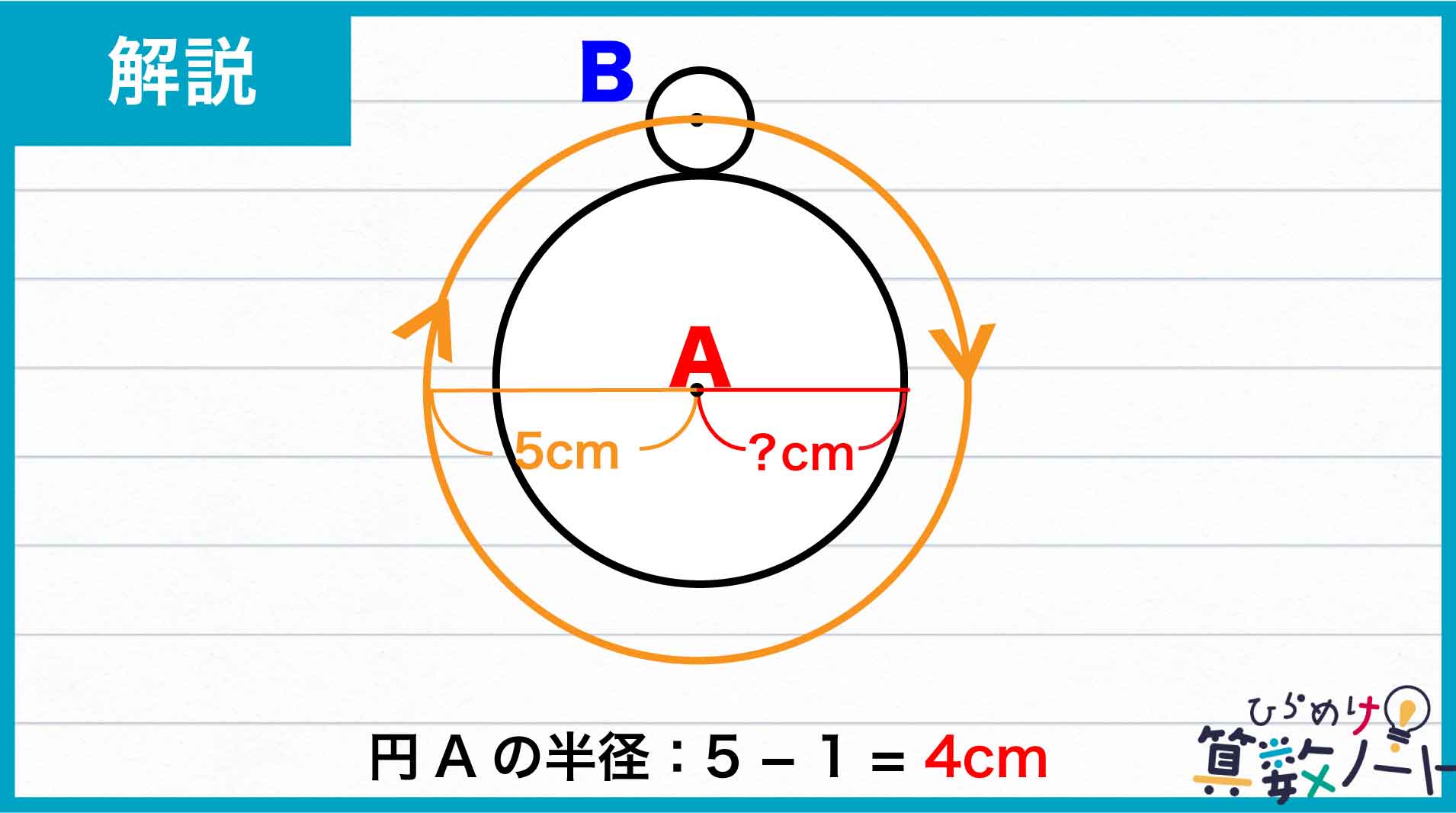
「円Bの回転数は中心の動いた長さで決まる」ということを踏まえて考えると、円Bが5回転するにはその中心が円周の5倍の長さを動かなければならないとわかります。中心が動いて描く円の半径は、円Aと円Bの半径の和に等しくなります。円Bの半径は1cmなので、中心が描く円の半径はその5倍、すなわち5cmです。したがって円Aの半径は、5-1=4cmであることがわかるのです。
答え:4cm
実際に転がしてみる
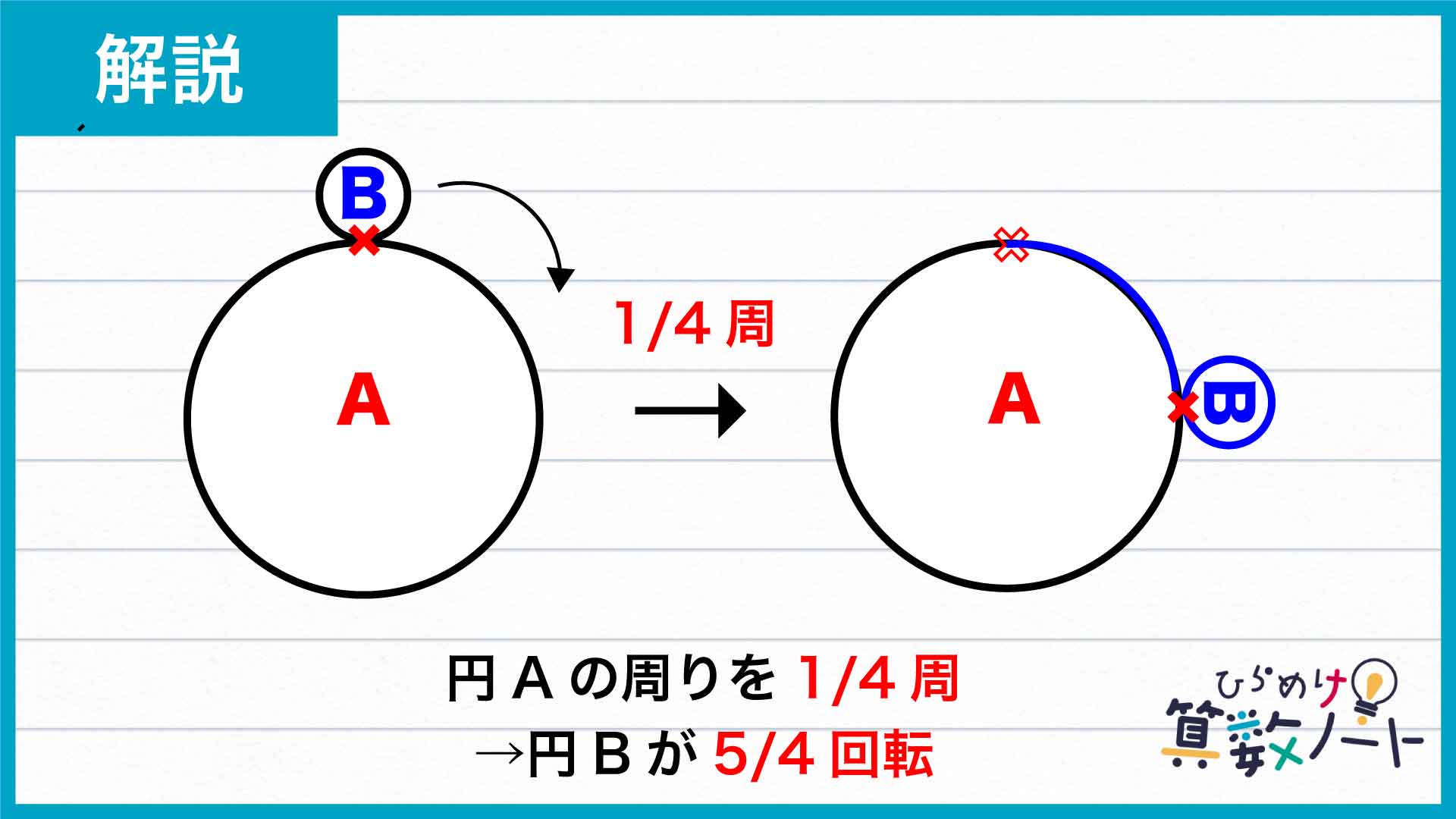
では最後に、半径4cmの円Aの周りで実際に円Bを転がしてみましょう。円Bが円Aの周りを4分の1周したときについて考えます。
円Aの円周の長さは円Bの4倍なので、4分の1周したときに円Bはちょうど円周と同じだけの長さをなぞり、転がす前と同じ点で円Aと接します。しかし円Bをよく見ると、転がす前の状態から4分の1回転した向きになっていることがわかります。実はこのとき、円Bは既に1+4分の1=4分の5回転しているのです。これを元の位置に戻るまで繰り返すので、円Bは合計で4分の5×4=5回転するというわけです。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







