解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
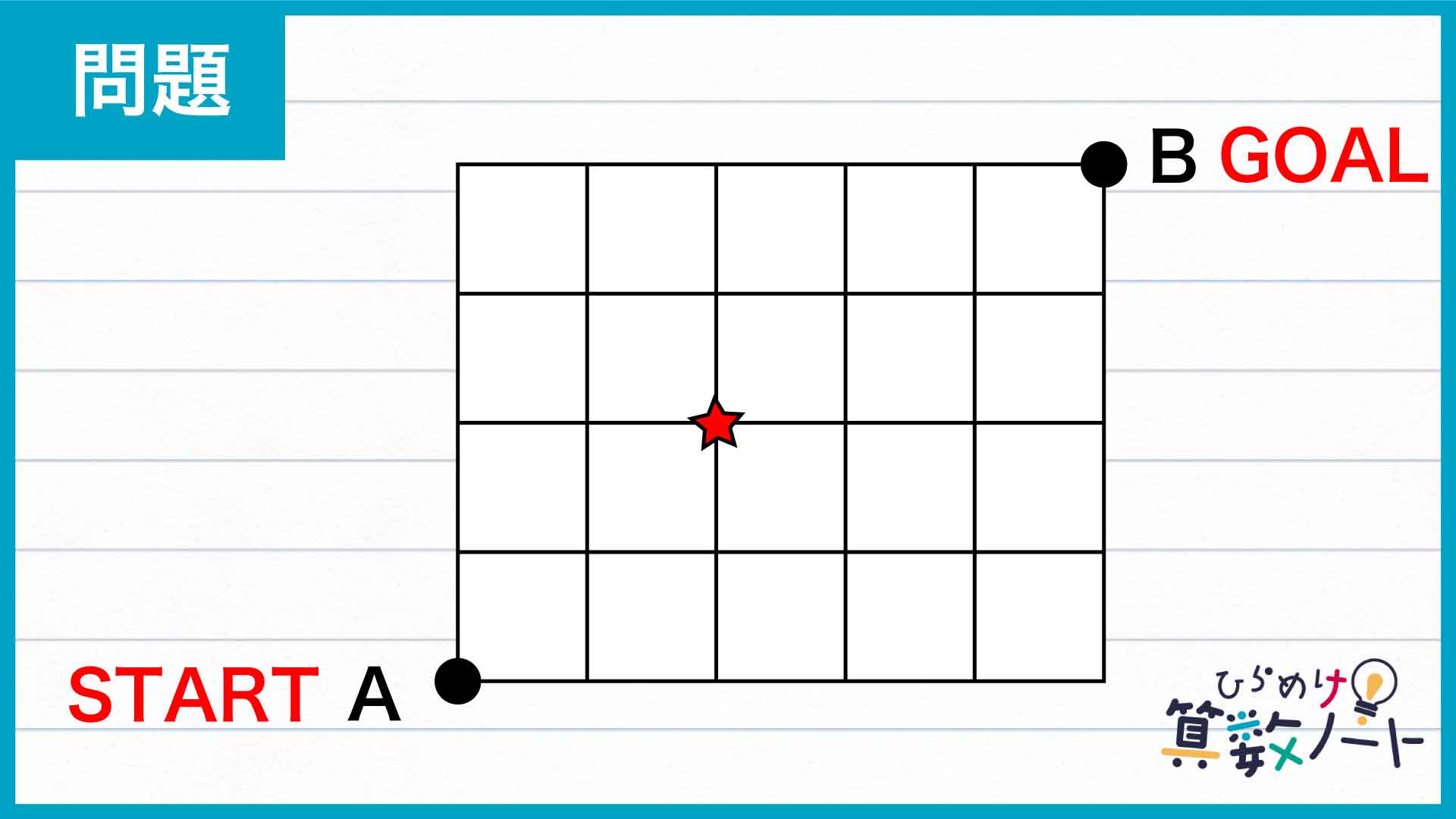
問題の解き方をまとめた図がこちらです。
ポイントは、マス目全体を2つの区間に分けた後で、各点への行き方を順番に考えることです。
では、この流れに沿って解いていきましょう!
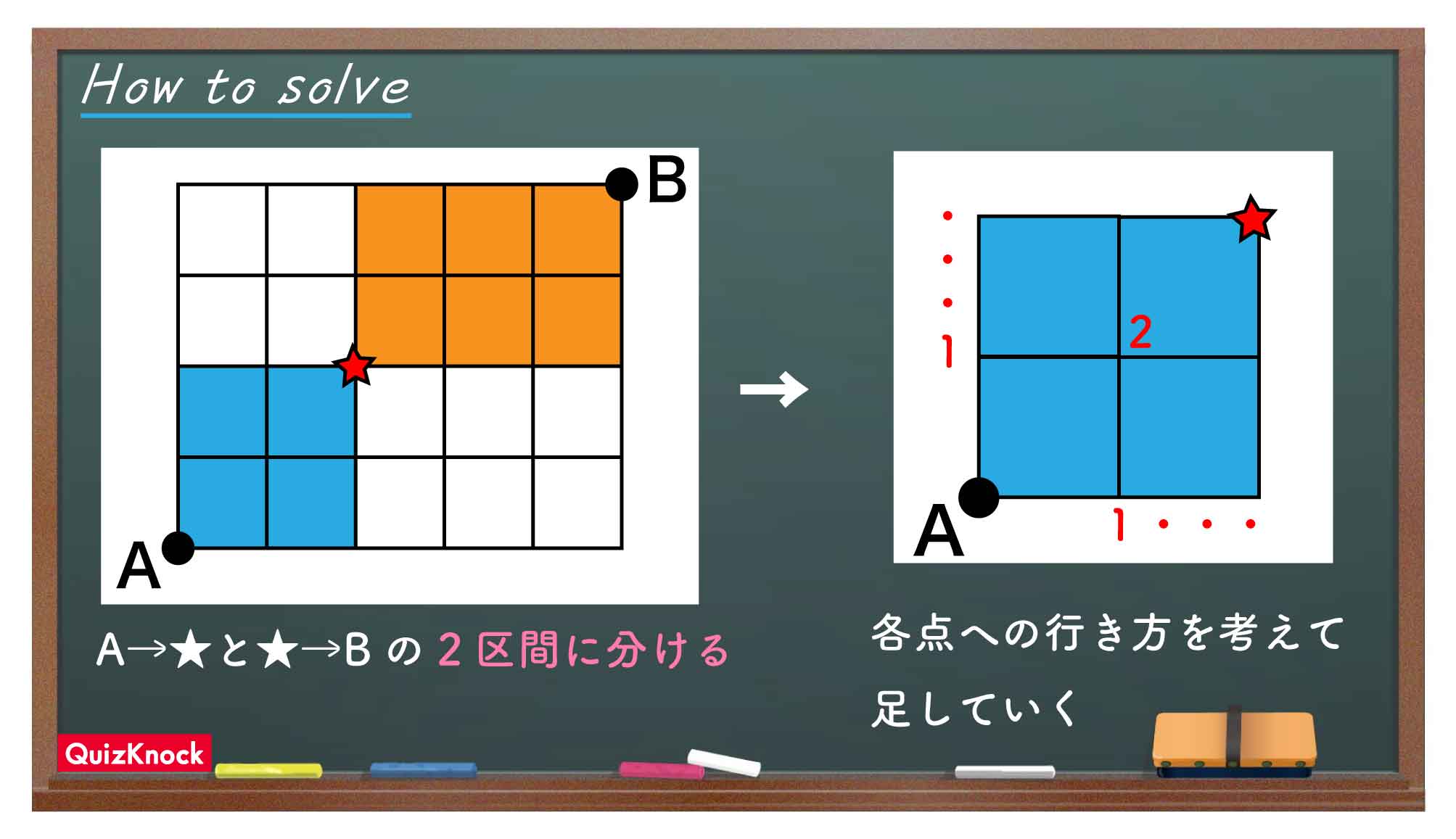
チェックポイントの前と後で分ける
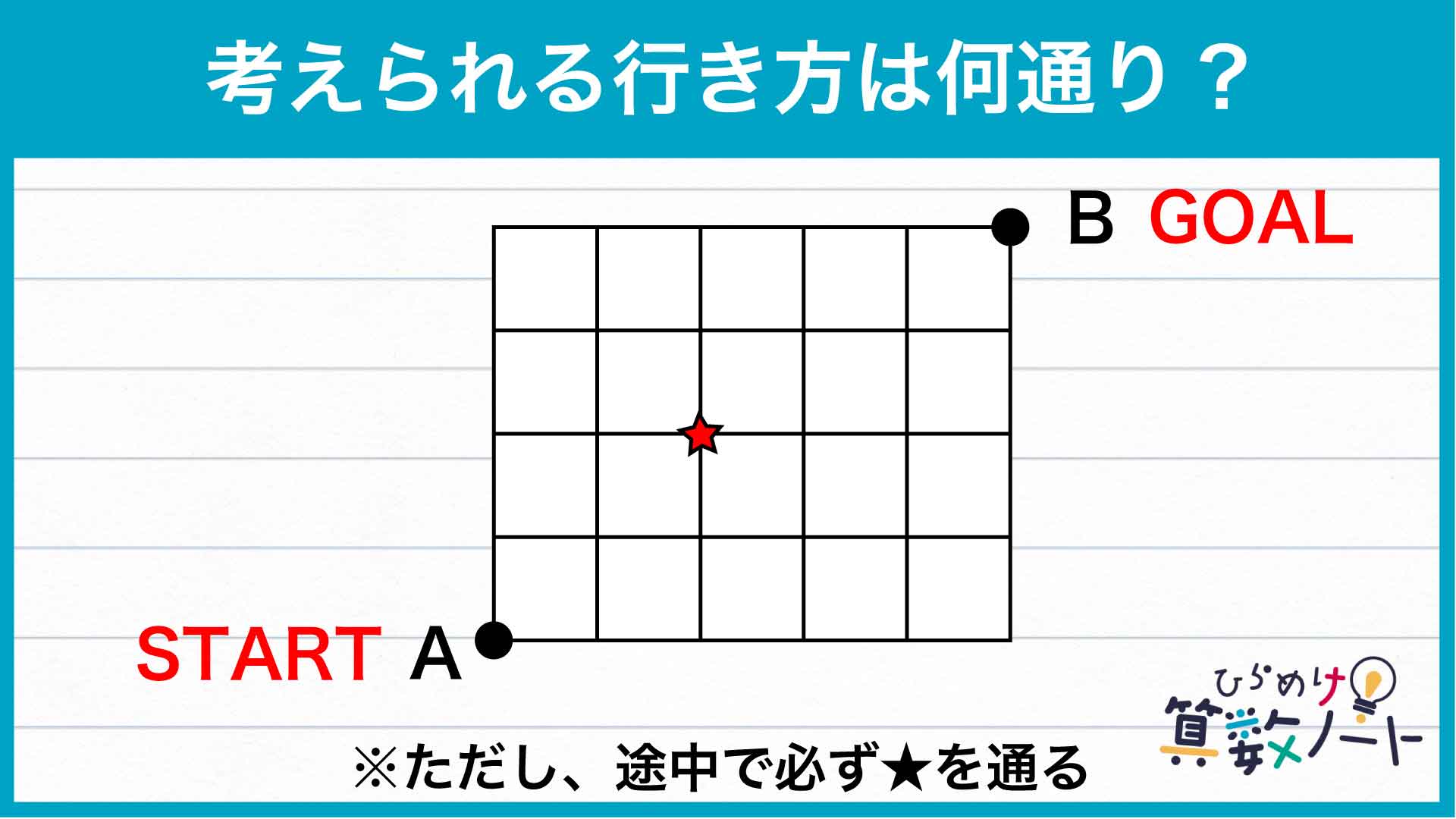
左下の点Aから右上の点Bへ遠回りせずに行くとき、途中で下や左へ動くことはありません。これは途中でチェックポイントを通る場合も同じです。
つまり、灰色に塗りつぶされたエリア(チェックポイントより上、または右にある点)から青のエリア(チェックポイントより下、または左にある点)へ移動することはあり得ず、前半の道順は青い4マスの範囲だけで考えればよいのです。
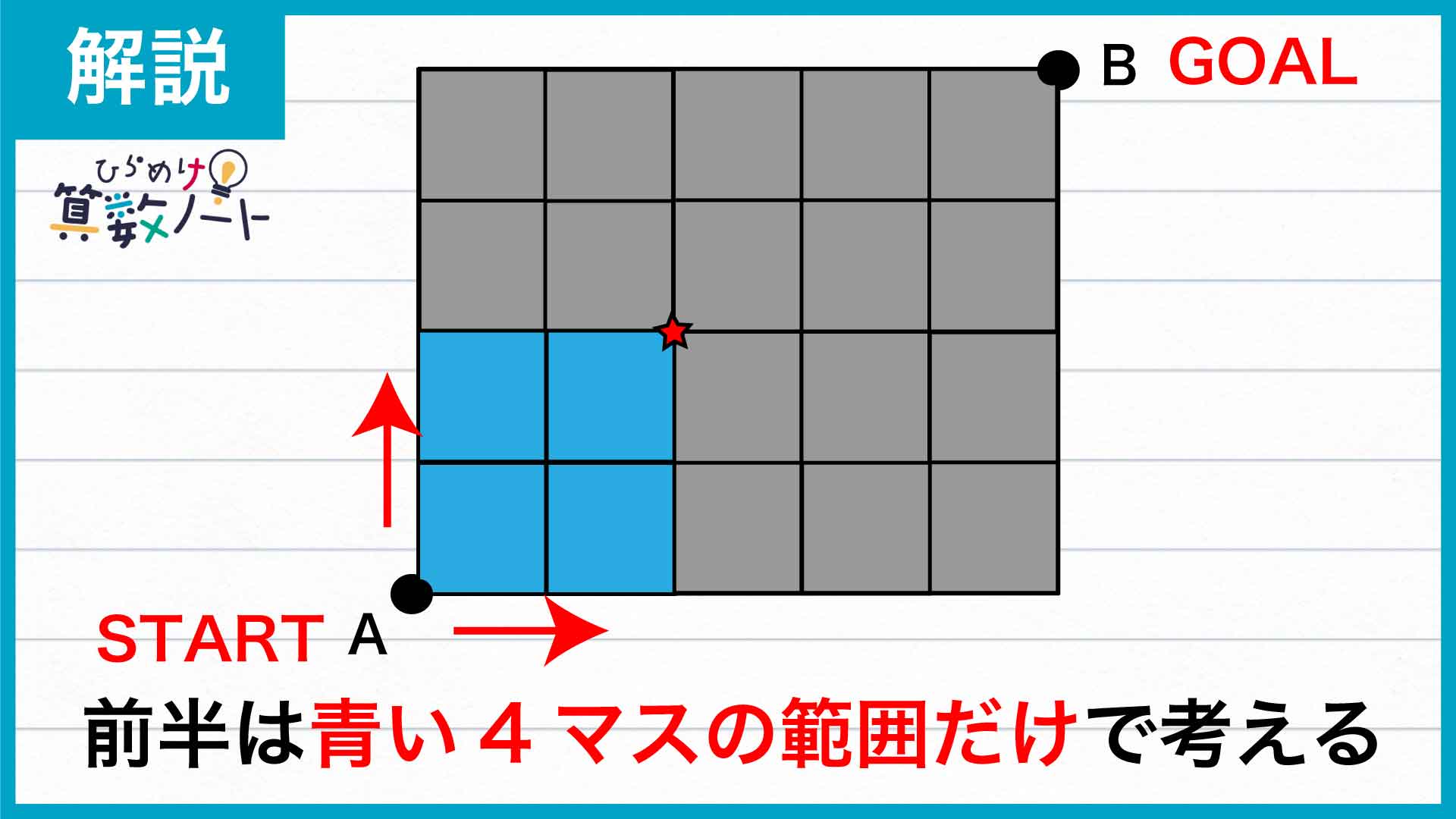
チェックポイントを通過した後は、やはり上か右かに動き続けてBを目指します。したがって後半の道順は、オレンジの6マスの範囲だけで考えればよいとわかります。
行き方をひとつずつ考える
まずAからチェックポイントへの行き方を考えましょう。Aを出発したあと、最初に通るのは図のaまたはbの点です。
これは、遠回りしないことを考えると、aまたはbへの行き方が「Aから右(上)に1マス分動く」の1通りであると言い換えることもできます。そこで、aとbそれぞれの位置に「1」とメモした上で、次の点への行き方を考えます。
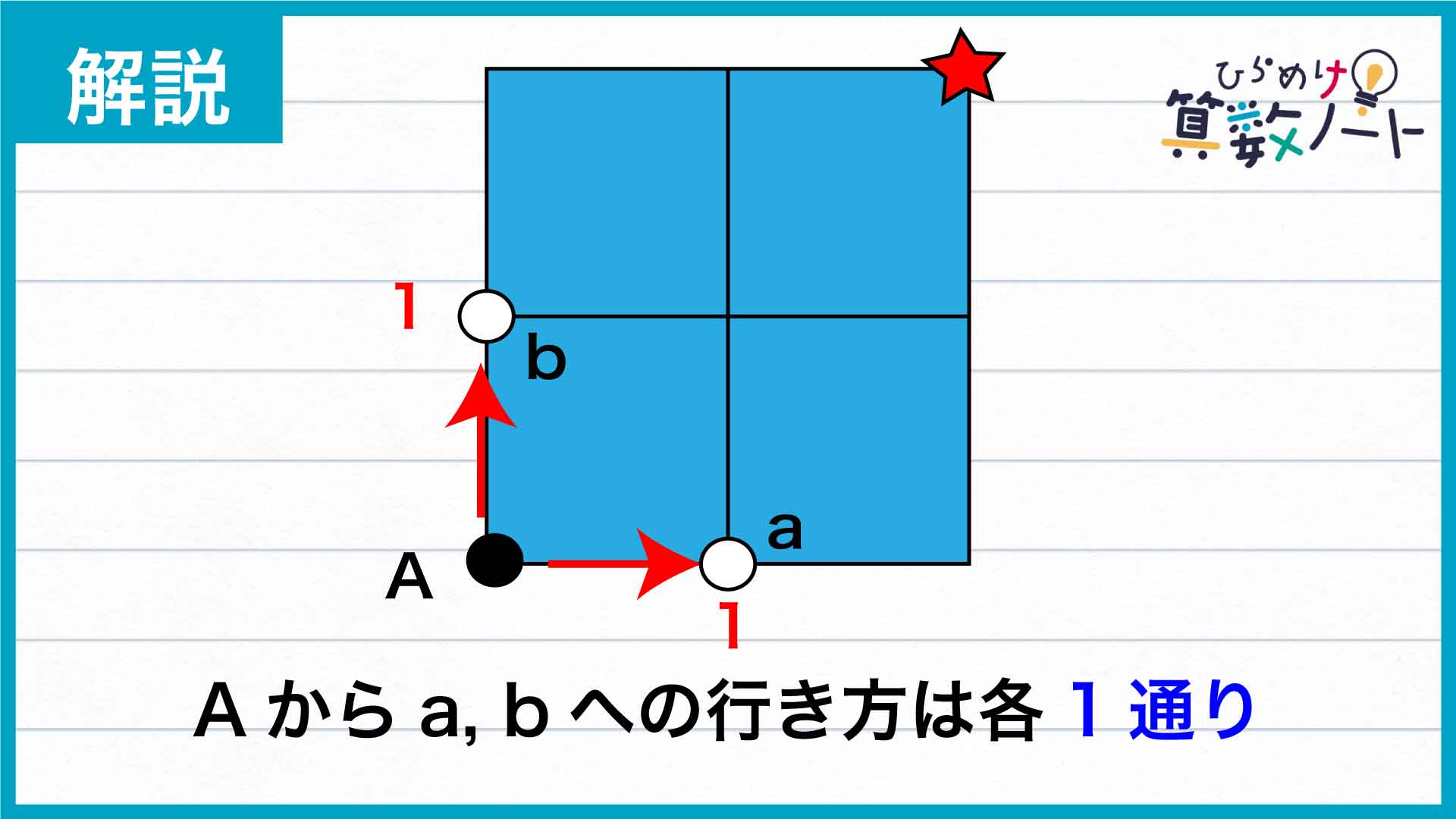
次の移動先としては、c、d、eの点が考えられます。cまたはeへの行き方は「a(b)から右(上)に1マス分動く」の1通りなので、そのまま「1」と書いておきます。
一方dへは、aから上に移動してもbから右に移動しても行くことができるので、Aからの行き方を考えると1+1=2通りあることがわかります。
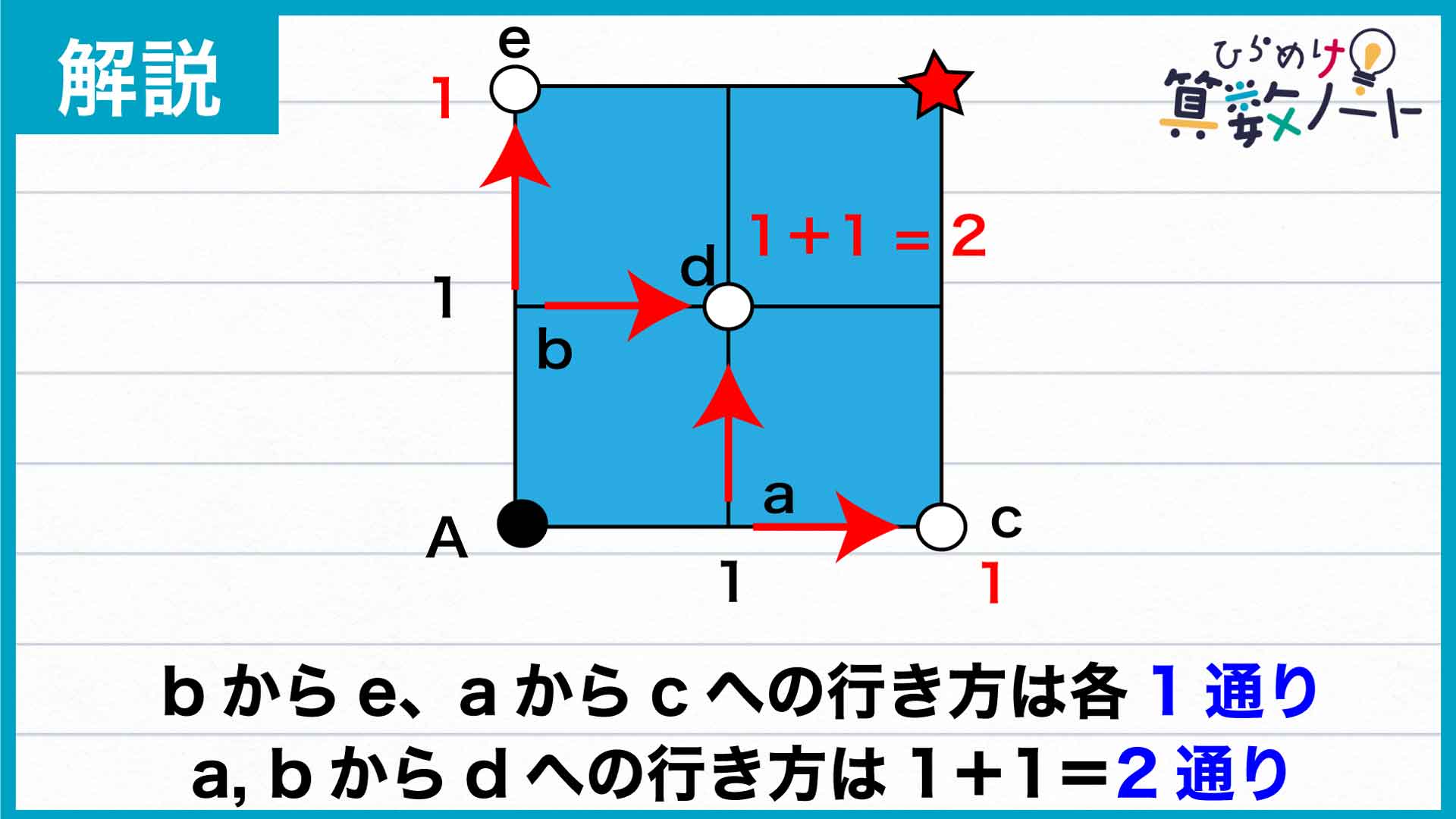
同じようにして次の点f、gへの行き方を考えると、cまたはd(eまたはd)から1マスの移動で行けるので、Aからの行き方はそれぞれ1+2=3通りあるとわかります。
そしてチェックポイントへはfまたはgから1マス移動することでたどり着くので、Aからの行き方は3+3=6通りです。
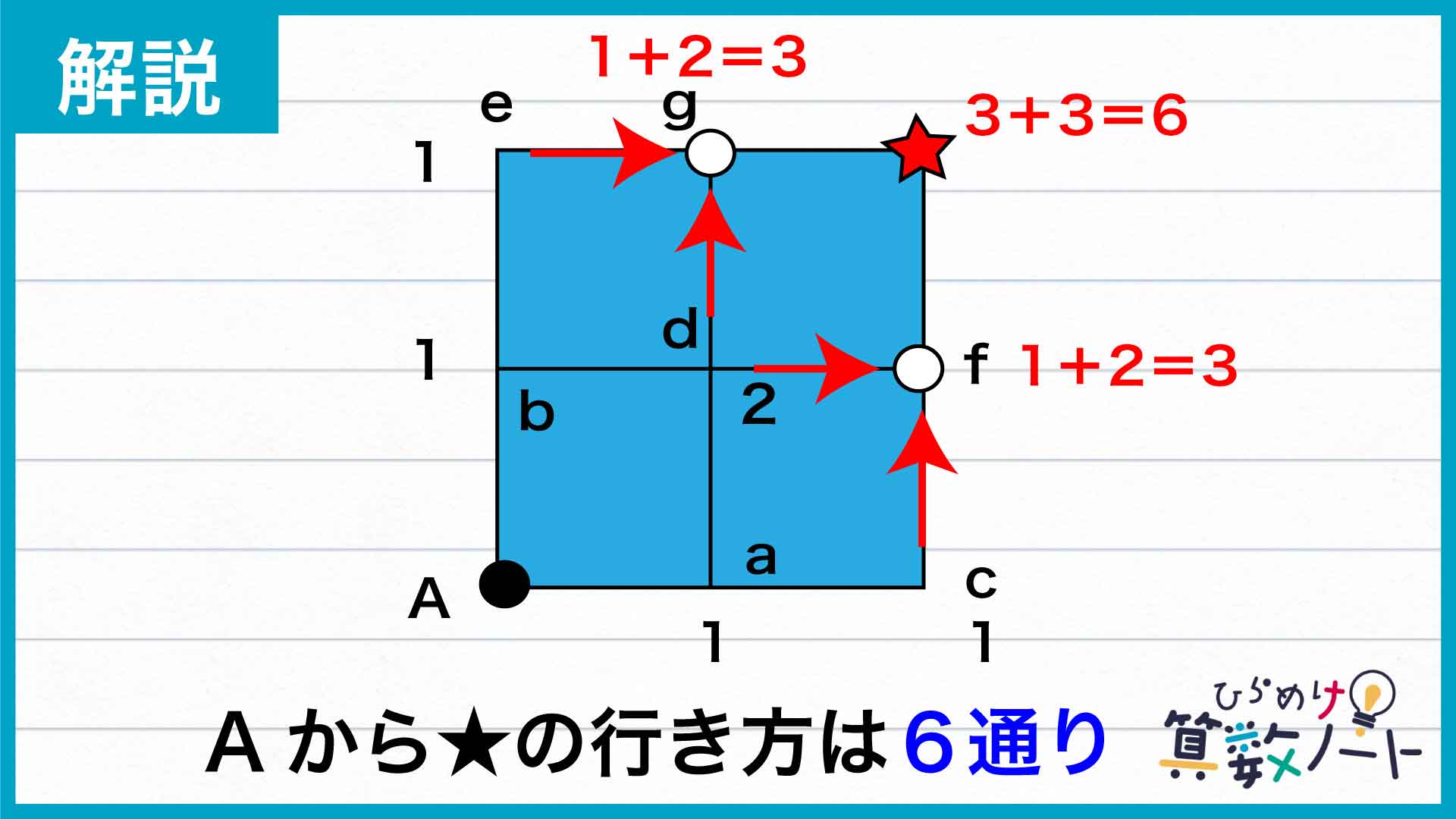
Aからチェックポイントへの行き方は、6通りあることがわかりました。チェックポイントからBへ向かう区間も、同様に考えます。
「チェックポイントからある点への行き方=目標地点の左隣の点への行き方+目標地点の真下の点への行き方」であることに基づいてどんどん数字を書き込んでいくと、図のようになります。
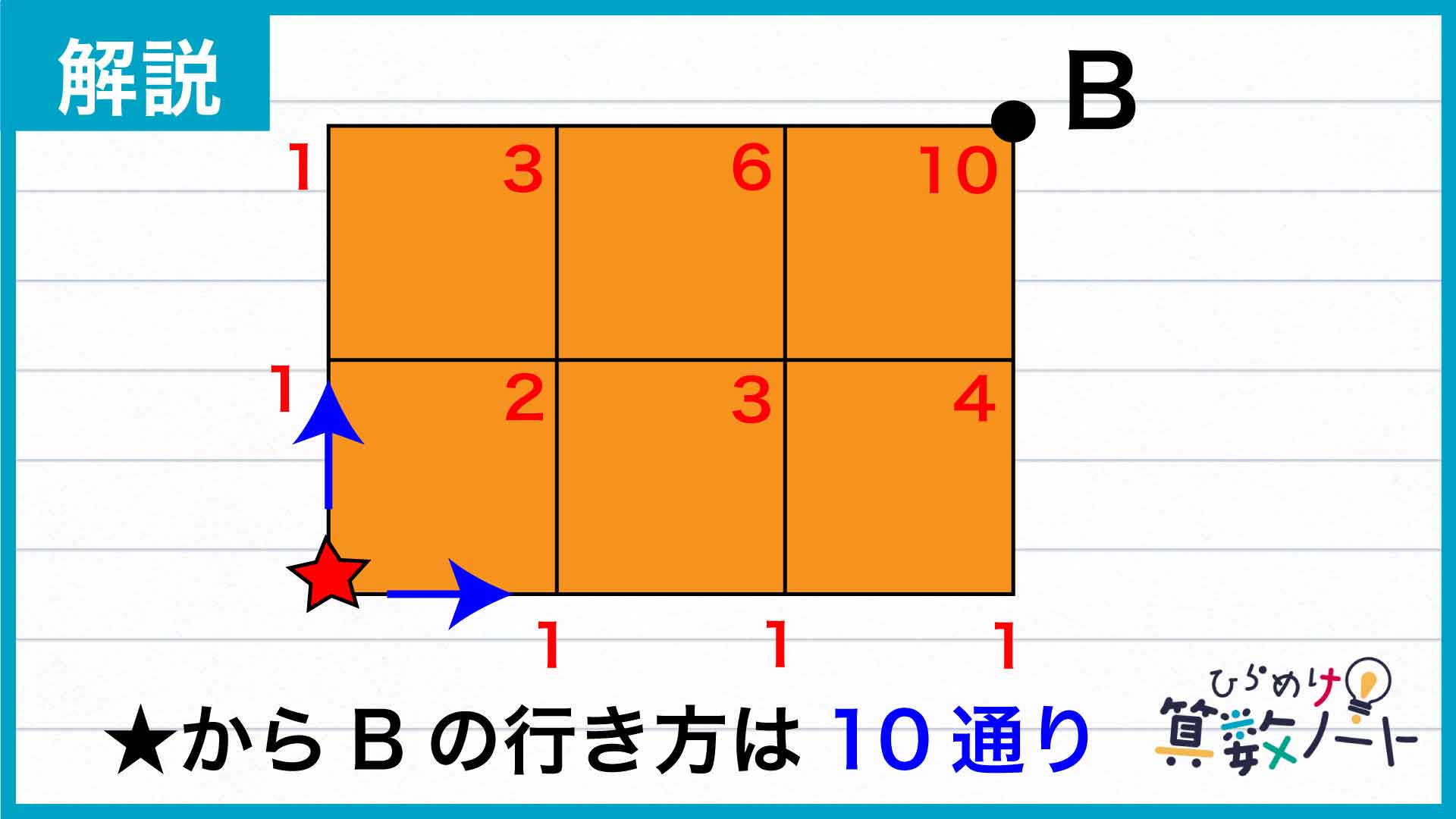
チェックポイントからBへの行き方は10通りあることがわかりました。つまり、Aからチェックポイントまでの6通りの行き方それぞれに対し、続くBへの行き方が10通りあるということになります。
したがって、Aからチェックポイントを通りBへ到達するまでの行き方は、6×10=60通りあるとわかります。
答え:60通り
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)










.jpg)







