解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
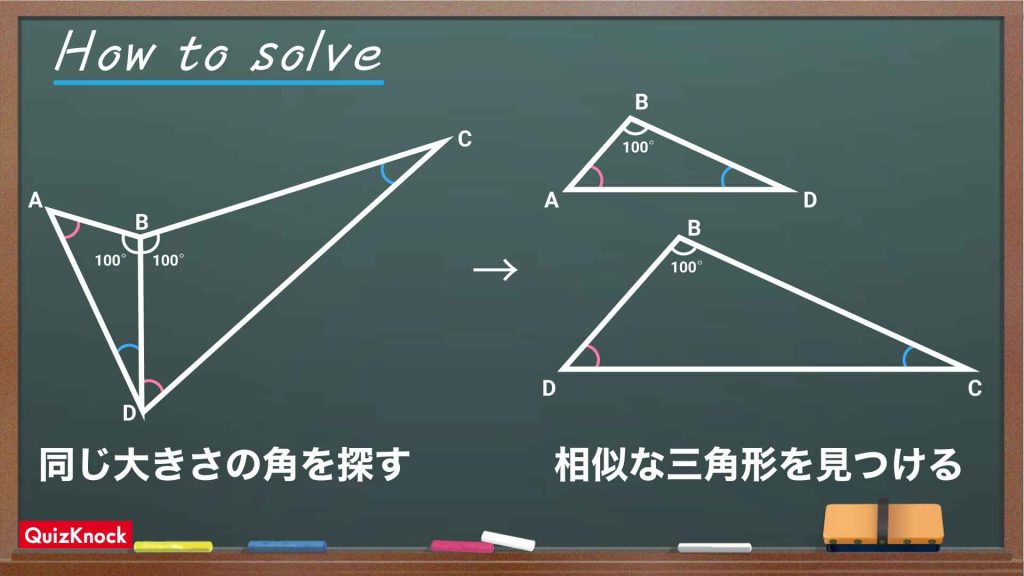
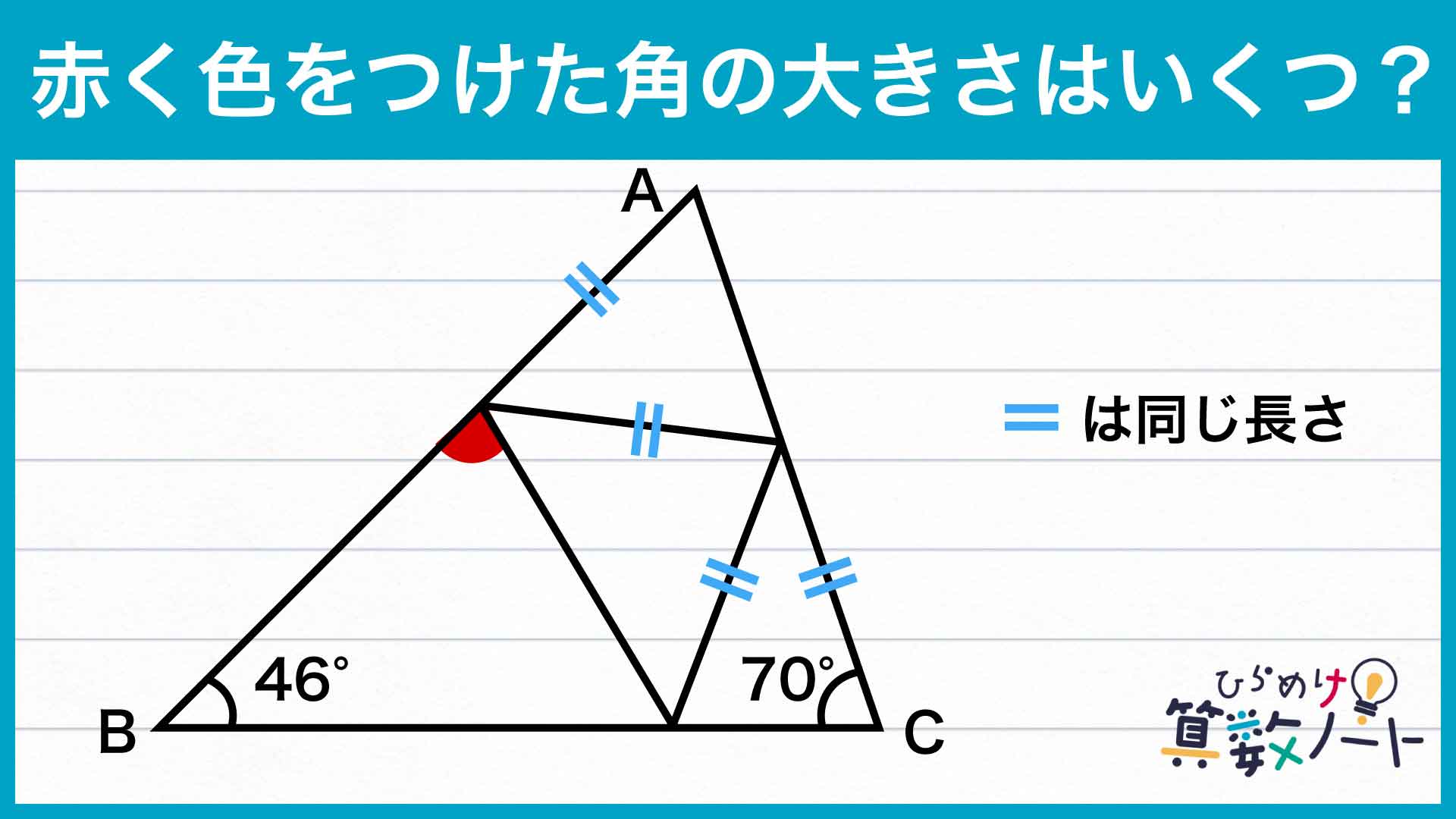
今回の問題の解き方をまとめた図がこちらです。ポイントは同じ大きさの角を探し、相似な三角形を見つけることです。
この図の流れに沿って、解いていきましょう!
同じ大きさの角を探す
まずは、同じ大きさの角を探していきましょう。
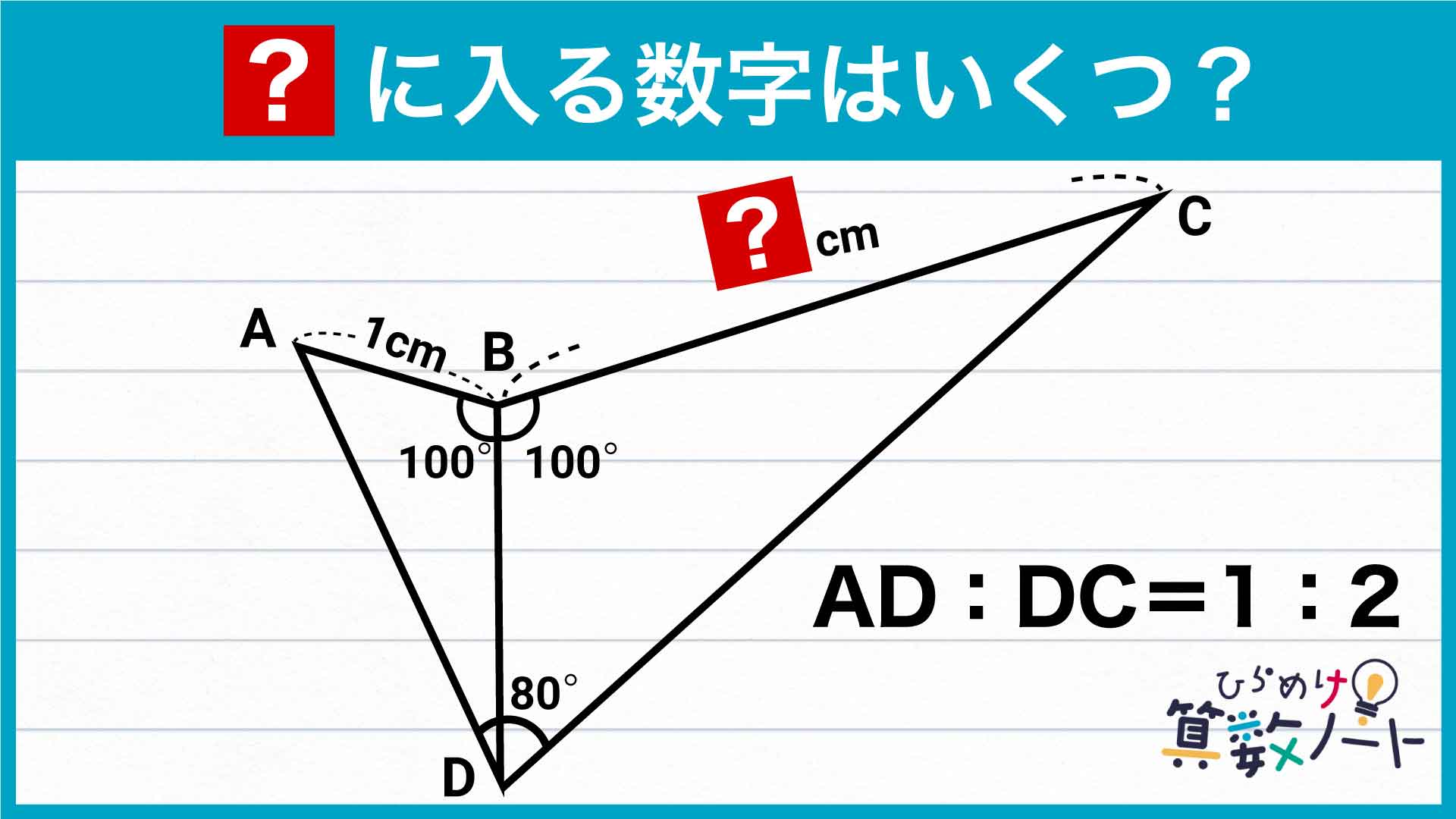
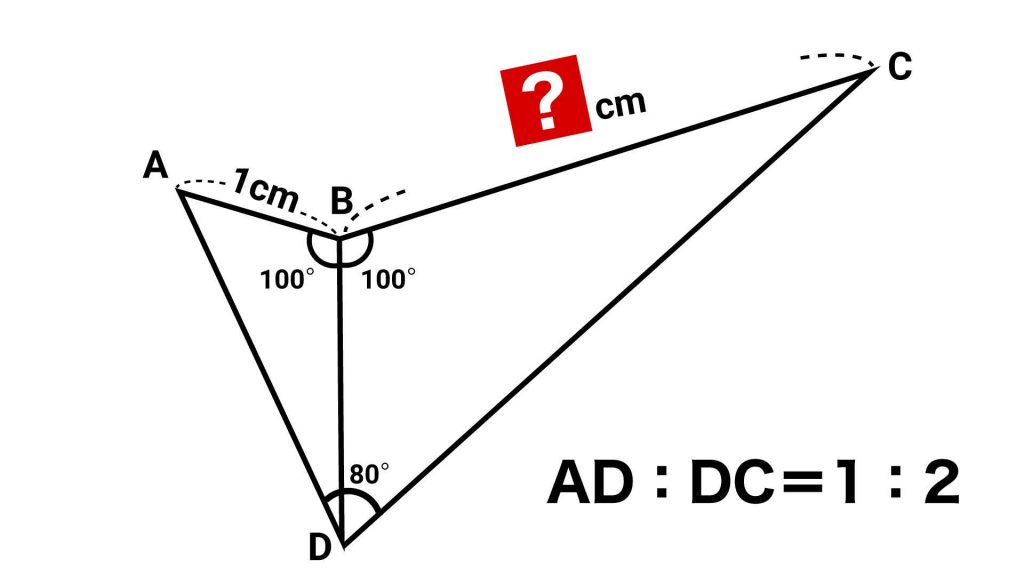
今のところ、角の大きさが具体的にわかっているのは、角ABD、角DBC、角ADCのみです。その他の角については、具体的な角度の大きさを簡単には求めることができません。
そこで、角ADBの大きさを用いて、それぞれの角の大きさを表すことを考えます。
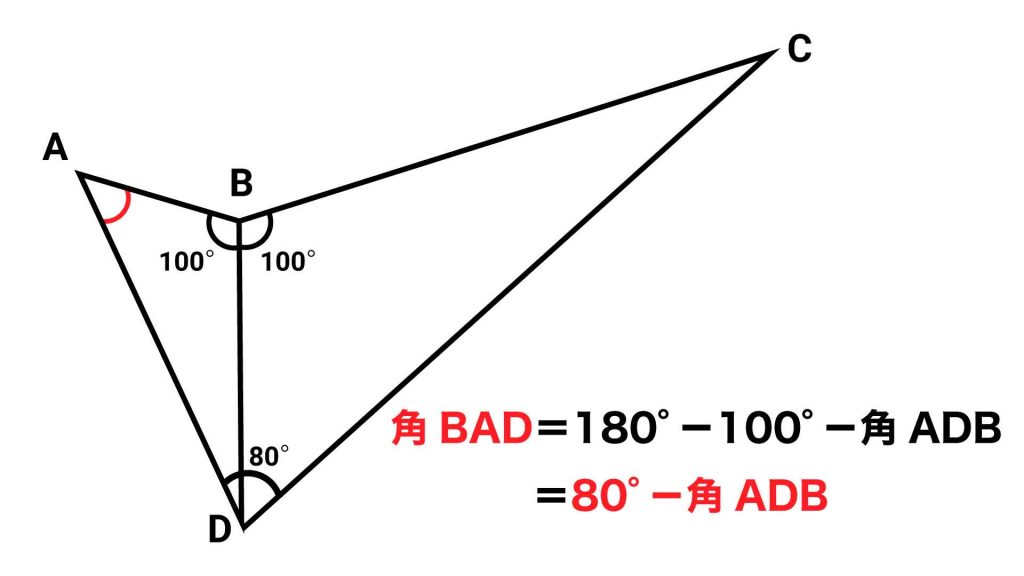
まず角BADの大きさは、三角形ABDの内角の和が180度であることから、180-100-角ADB=80-角ADBと表すことができます。
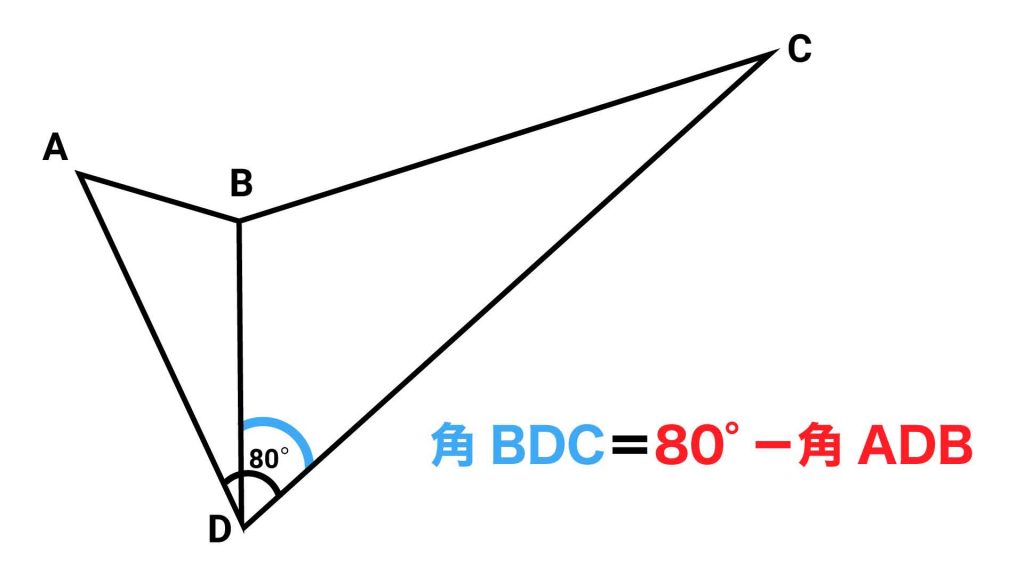
次に、角BDCの大きさは、角ADCの大きさが80度であることから、80-角ADBと表せます。
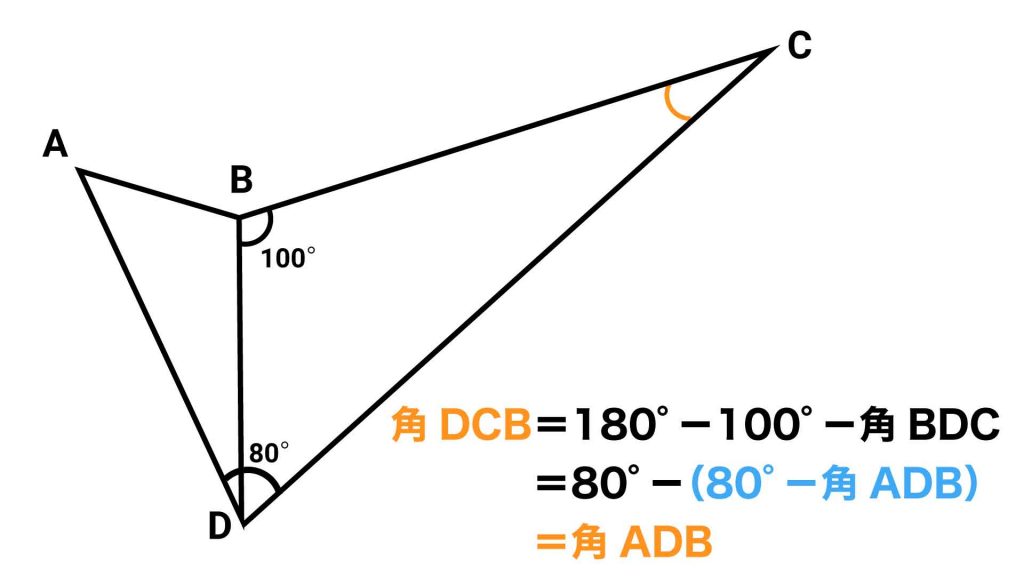
最後に角DCBの大きさは、三角形DBCの内角の和が180度であることから、180-角DBC-角BDC=180-100-(80-角ADB)=角ADBと表すことができます。
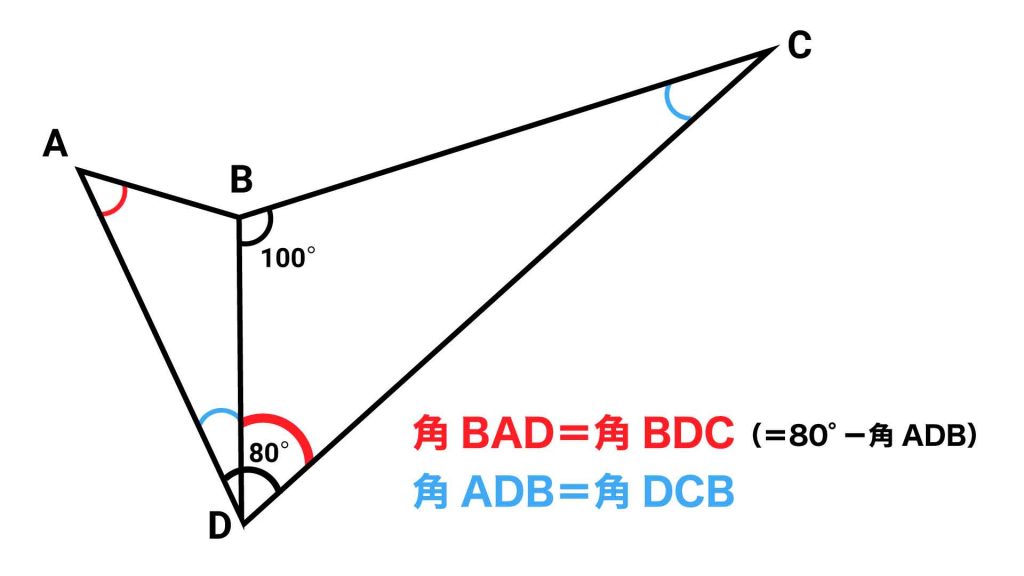
以上の結果から、角BADと角BDC、角ADBと角DCBの大きさがそれぞれ等しいことがわかりました。
三角形ABDと三角形DBCの関係は?
三角形ABDと三角形DBCを比較すると、3つの内角の大きさがそれぞれ互いに等しいことから、相似の関係にあることがわかります。
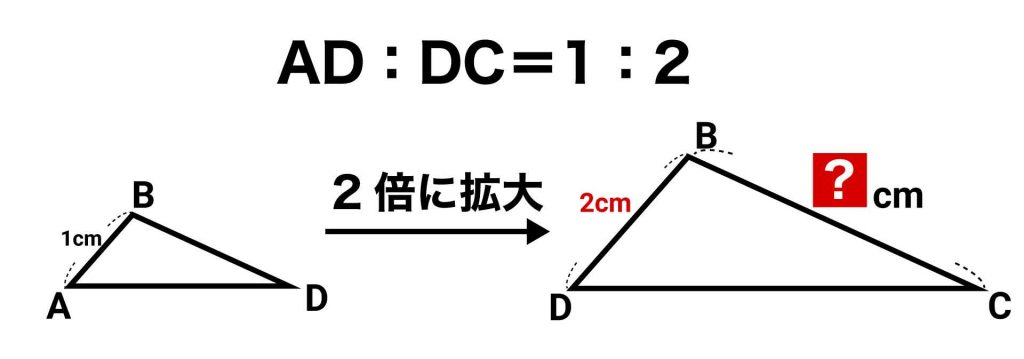
また、辺AD:辺DC=1:2であることから、三角形DBCは、三角形ABDを2倍に拡大した図形であることがわかります。したがって、辺ABの長さが1cmであることから、この辺に対応する三角形DBCの辺DBの長さは2cmとなります。
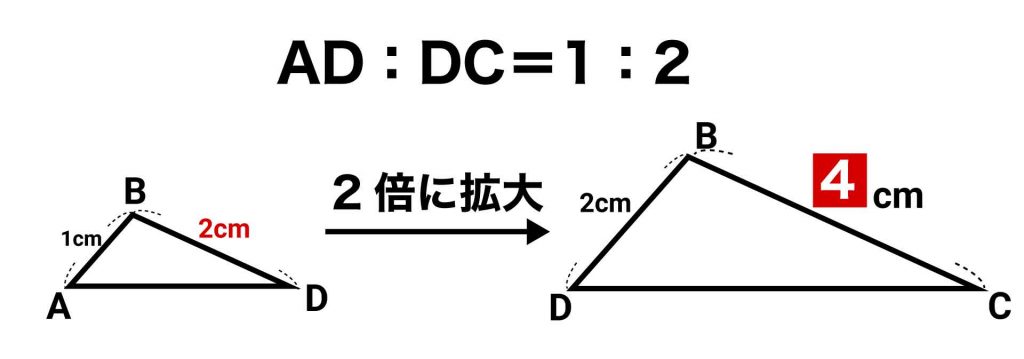
また、辺DBは三角形ABDの辺のひとつでもあり、この辺に対応する三角形DBCの辺は辺CBです。三角形DBCは三角形ABDを2倍に拡大した図形であることから、辺CBの長さは(辺DBの長さ)×2=2×2=4cmとなります。
答え:4cm
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】








.jpg)










.jpg)