解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
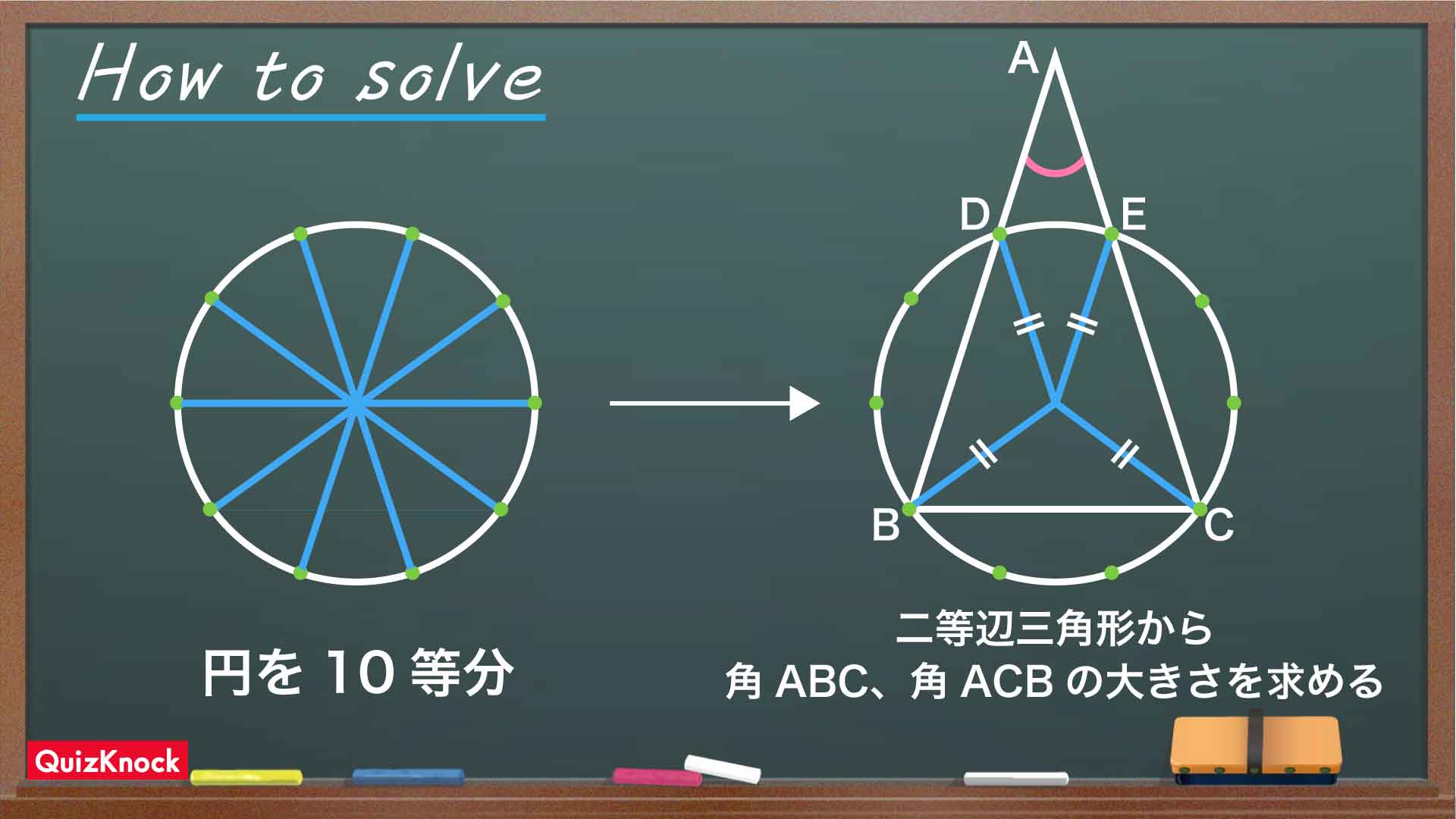
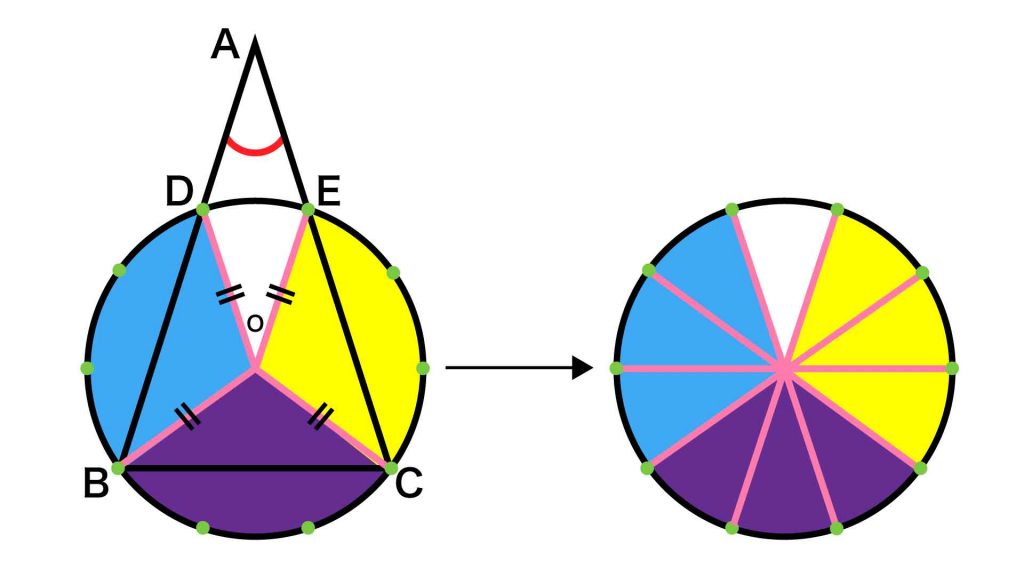
今回の問題の解き方をまとめた図がこちらです。
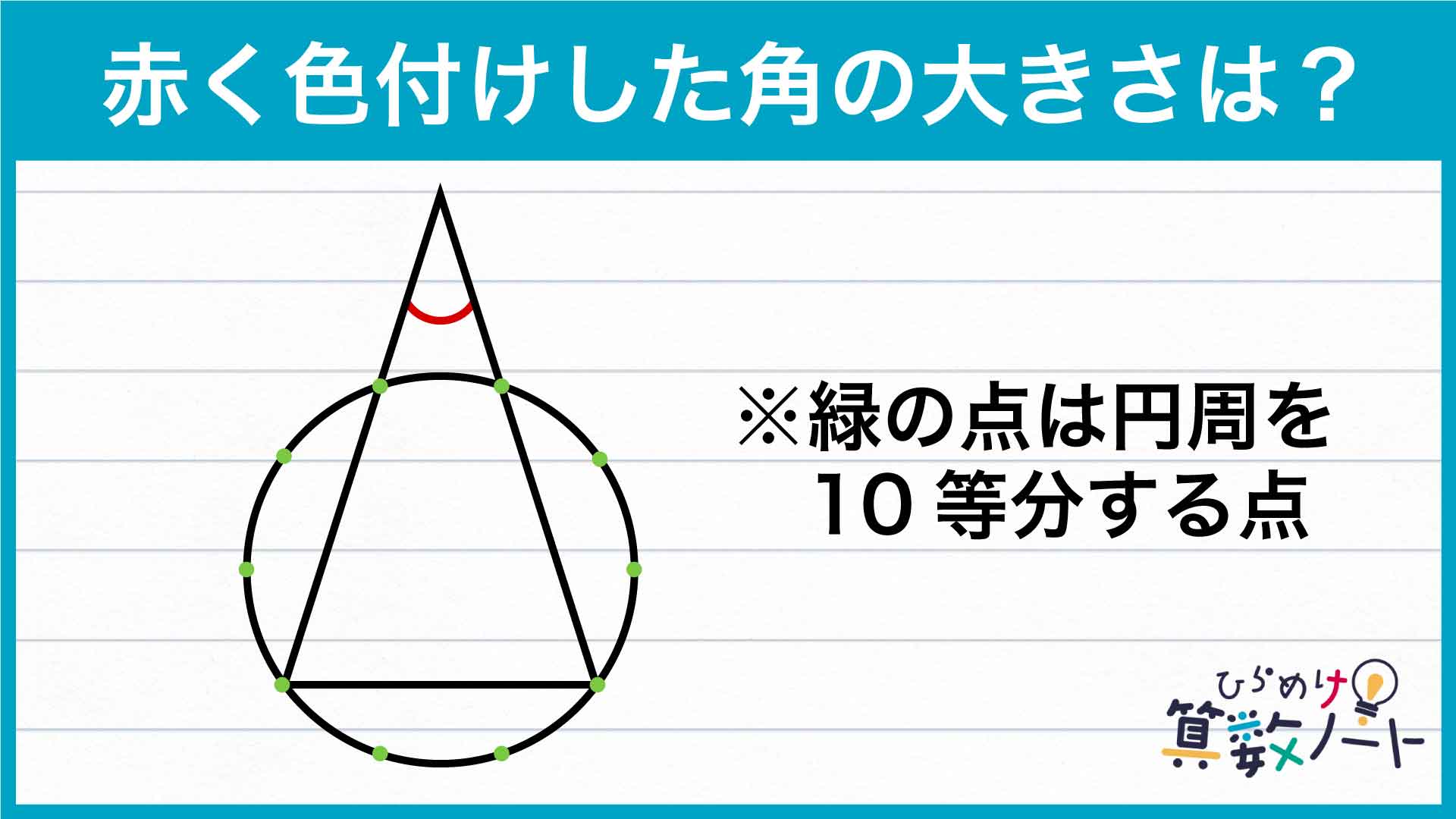
問題の角度を求めるには、三角形のほかの2つの角度がわかればよいのですが、問題文には角度が書かれておらず、どうにかして探し出さなければなりません。ポイントは、「10等分された点と円の中心を結び、二等辺三角形を作る」こと。そうすることで、2つの角度を求めることができます。
この流れに沿って、解いていきましょう!
円の中心から線を引く
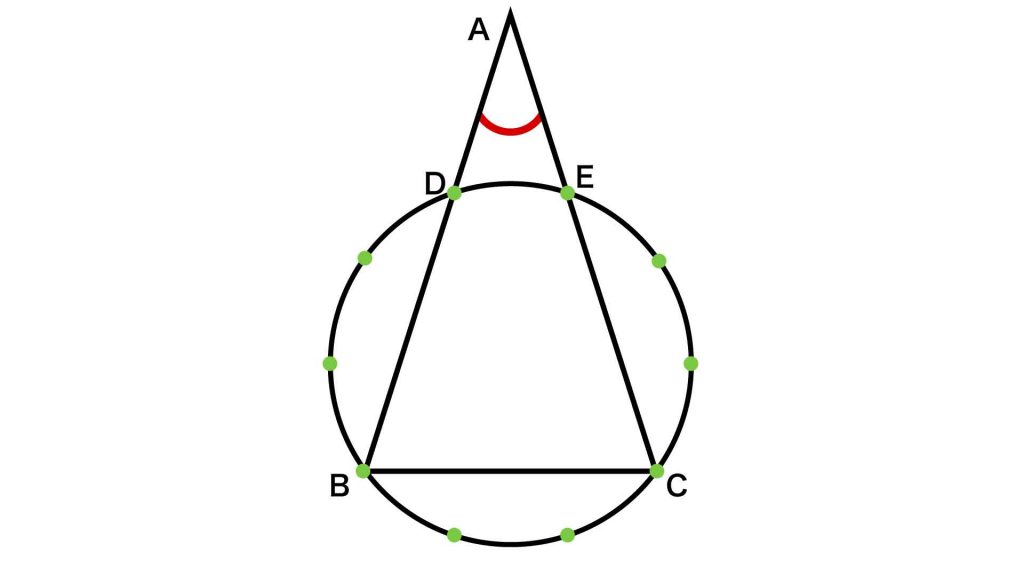
解説をわかりやすくするため、図のようにA、B、C、D、Eと置きます。
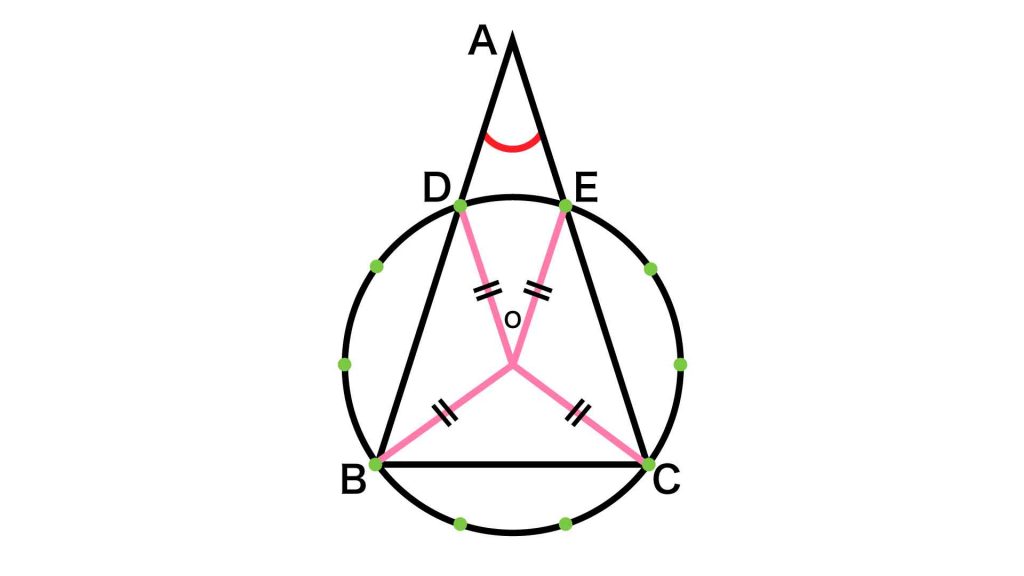
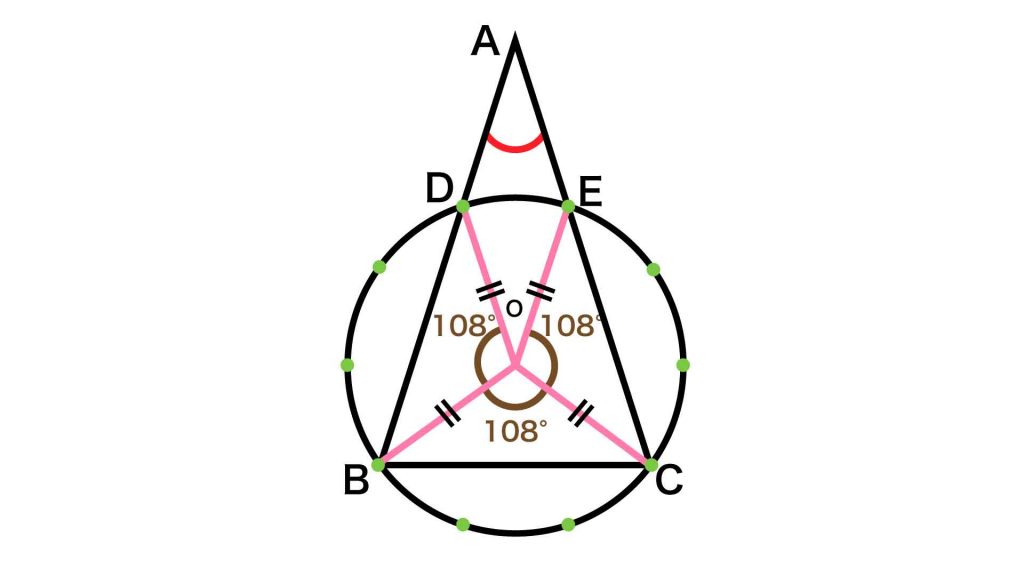
まずは、図のように線を引いてみましょう。円の中心をOと置きます。
線を引くことによってできる3つの扇形OBD、OBC、OCEは、いずれも円を10等分したおうぎ形3つ分にあたります。
よって各扇形の中心の角の大きさは、いずれも360÷10×3=108度となります。
三角形の2つの角を求める
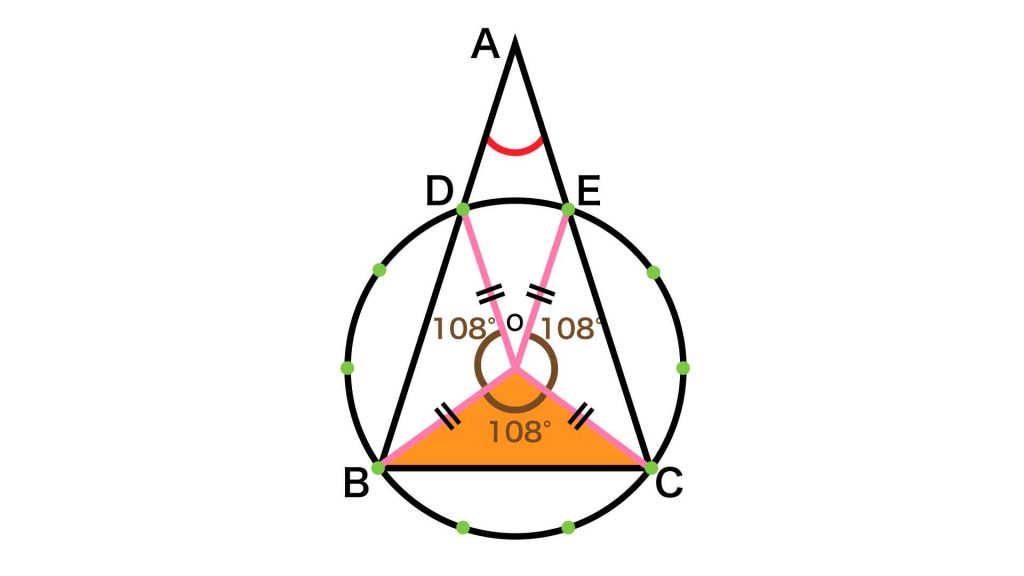
次に、オレンジ色の三角形OBCに注目します。
この三角形は、二辺が円の半径で構成されている二等辺三角形てす。角BOCの大きさが108度ですので、角OBCと角OCBの大きさはいずれも(180-108)÷2=36度とわかります。
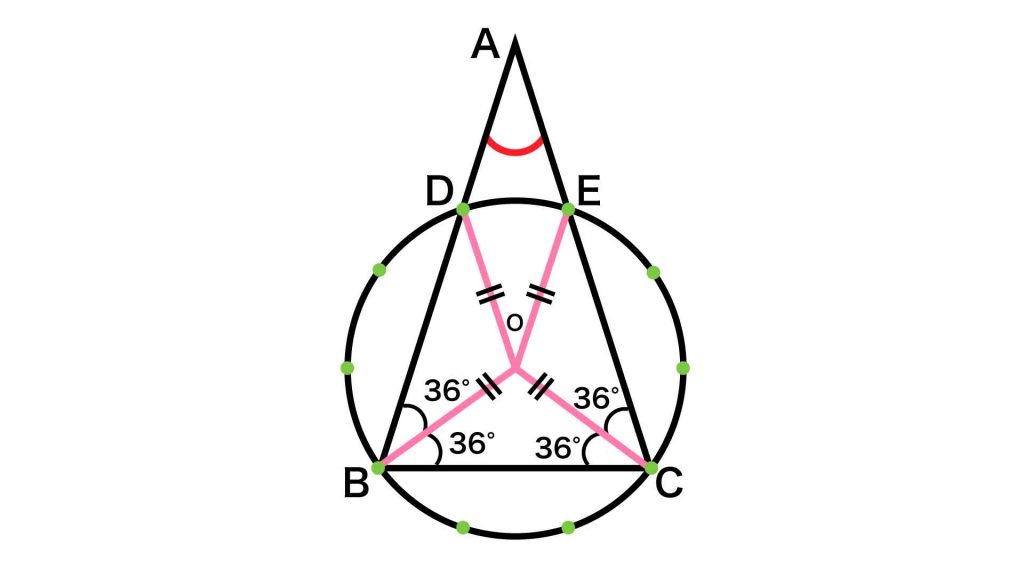
三角形OBD、OCEについても角BOD、COEがそれぞれ108度の二等辺三角形なので、角OBD、OCEの大きさは36度となります。
三角形ABCのうち、角ABCと角ACBの大きさはそれぞれ36×2=72度と求められます。したがって求める角度BACの大きさは、180-72-72=36度となります。
答え:36度
それでは、次回の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







