解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
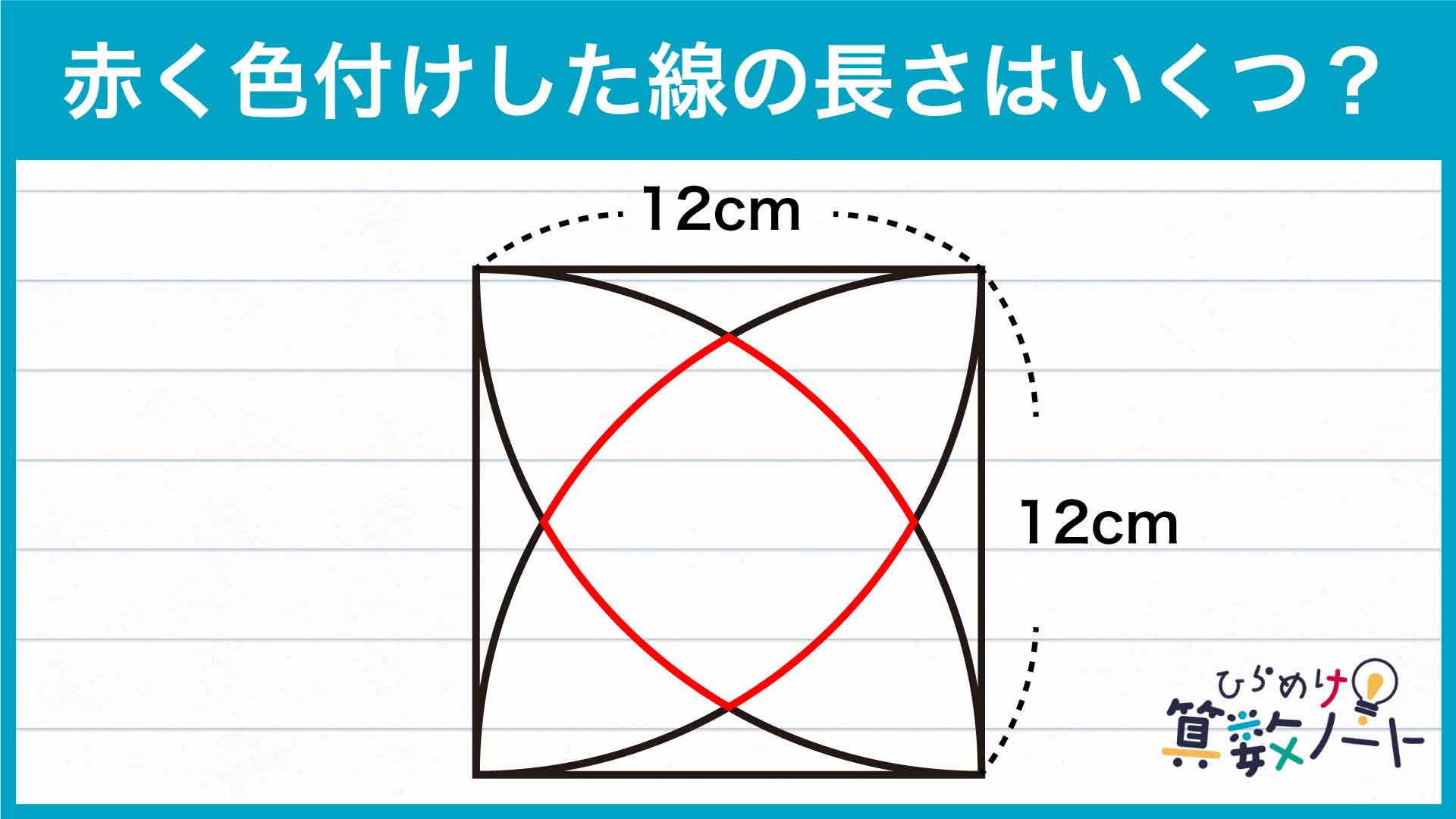
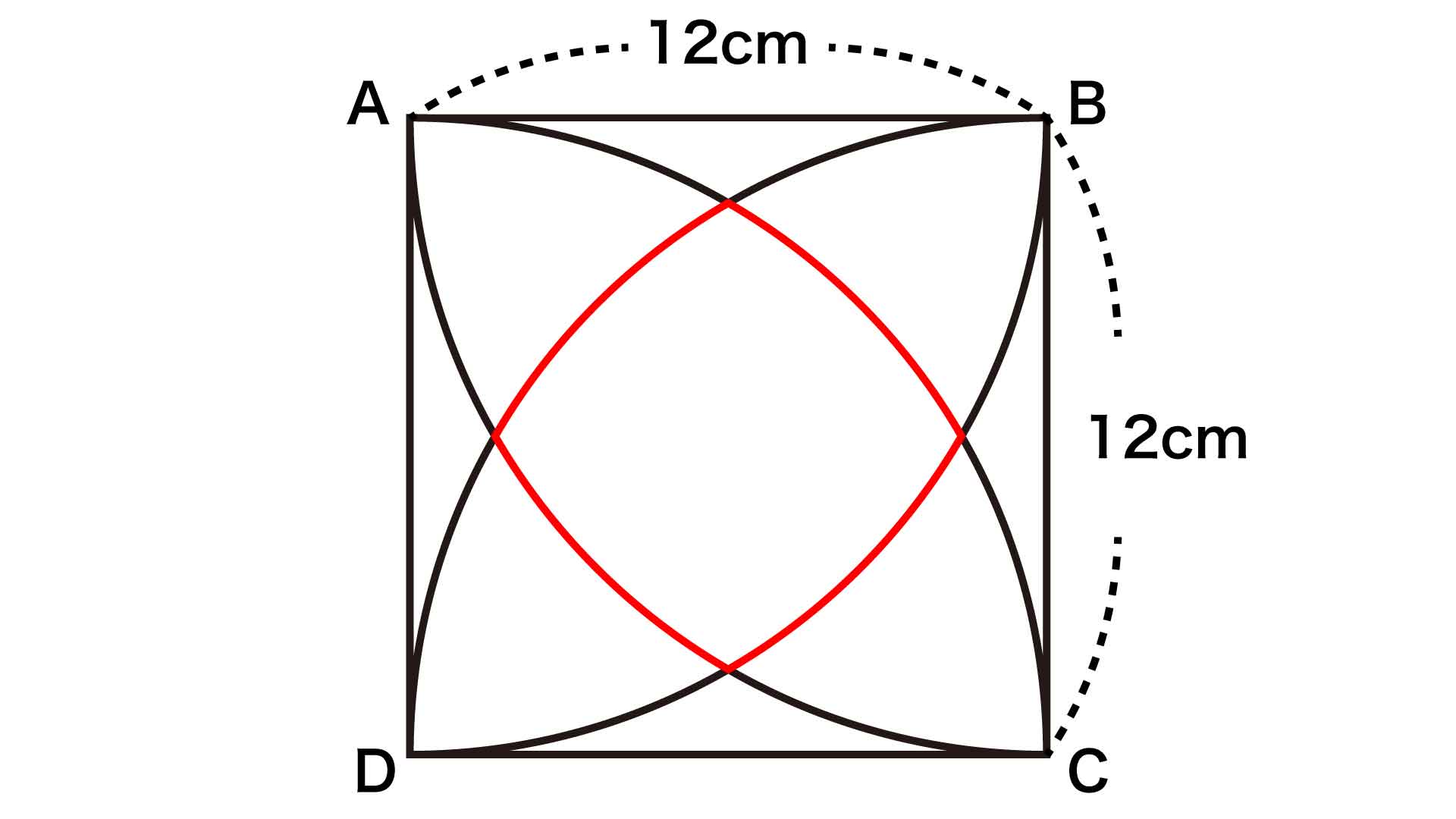▲（問題再掲）
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです。
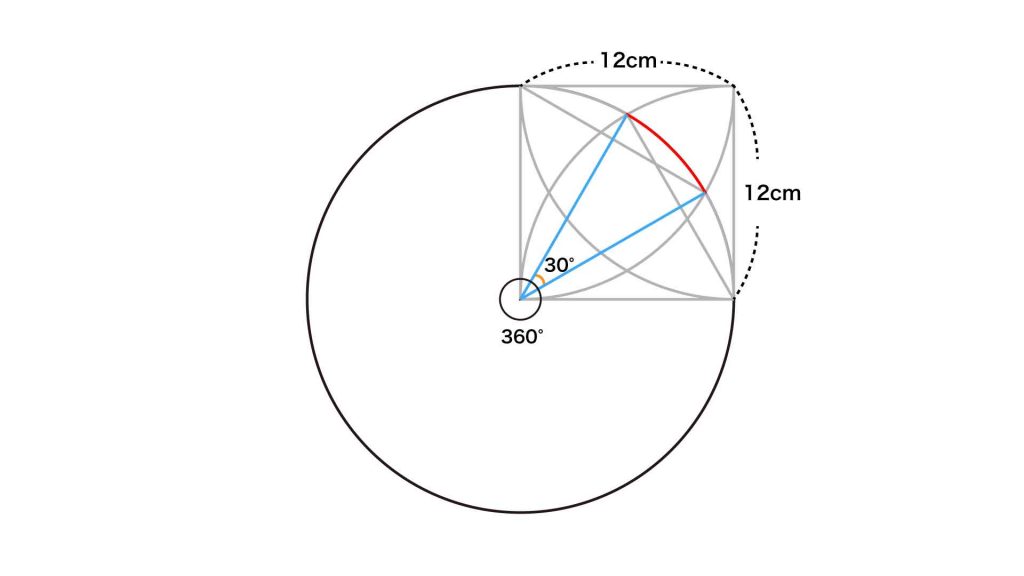
今回の解き方をまとめた図がこちらです。
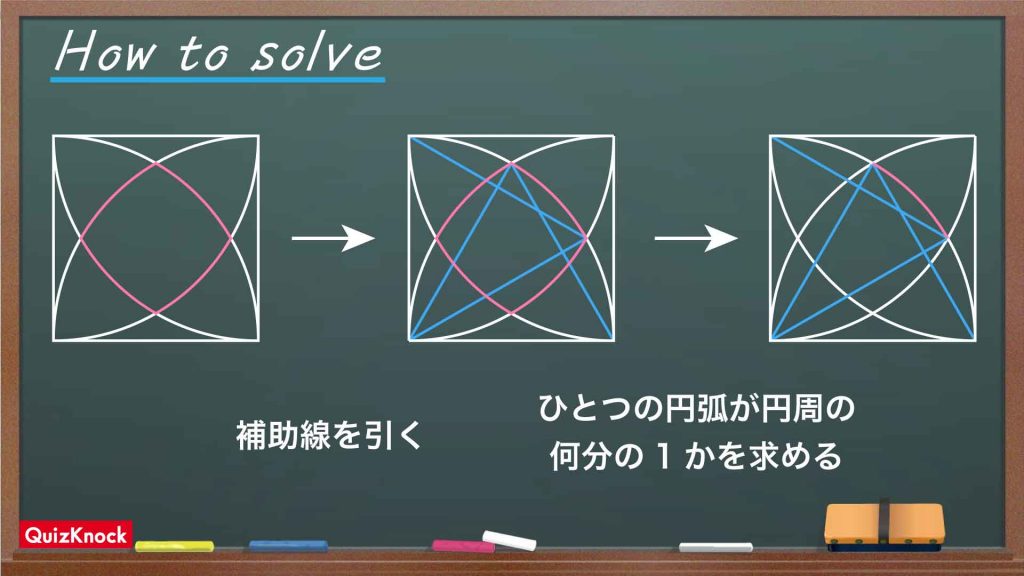
ポイントは、「弧の長さが円周の何分の1の長さにあたるかを調べる」ことです。
赤い線は同じ長さの弧が4つ集まったものです。そのため、ひとつの弧の長さを求め、その長さを4倍することで答えを導くことができます。
そして、ひとつの弧の長さは、その弧を持つ扇形の中心角の大きさがわかれば求めることができます。
この流れに沿って、問題を攻略していきましょう！
補助線を引く
まずは、以下の図の青色の線のように補助線を引きます。
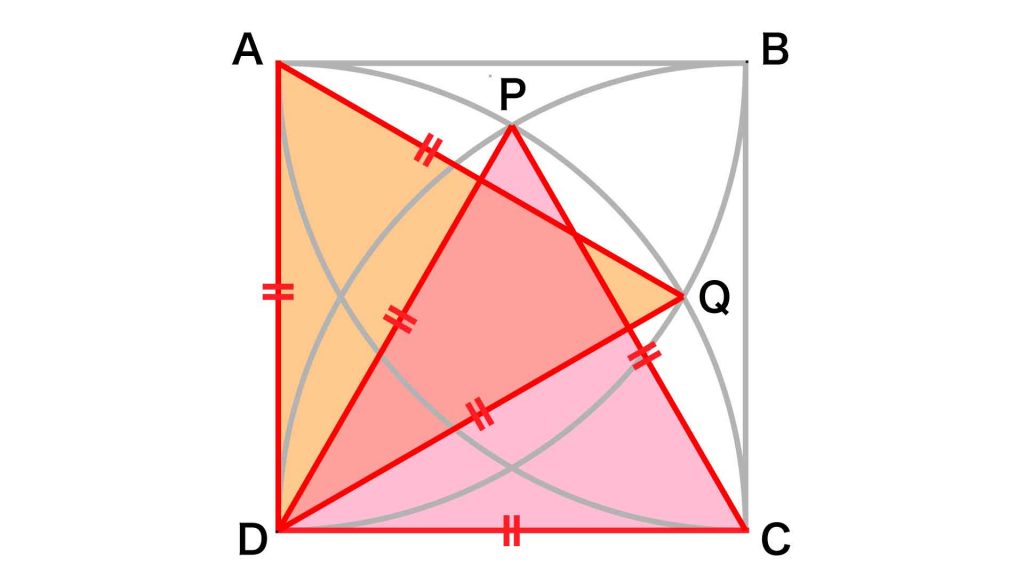
また、以下の図の2点をP、Qとします。
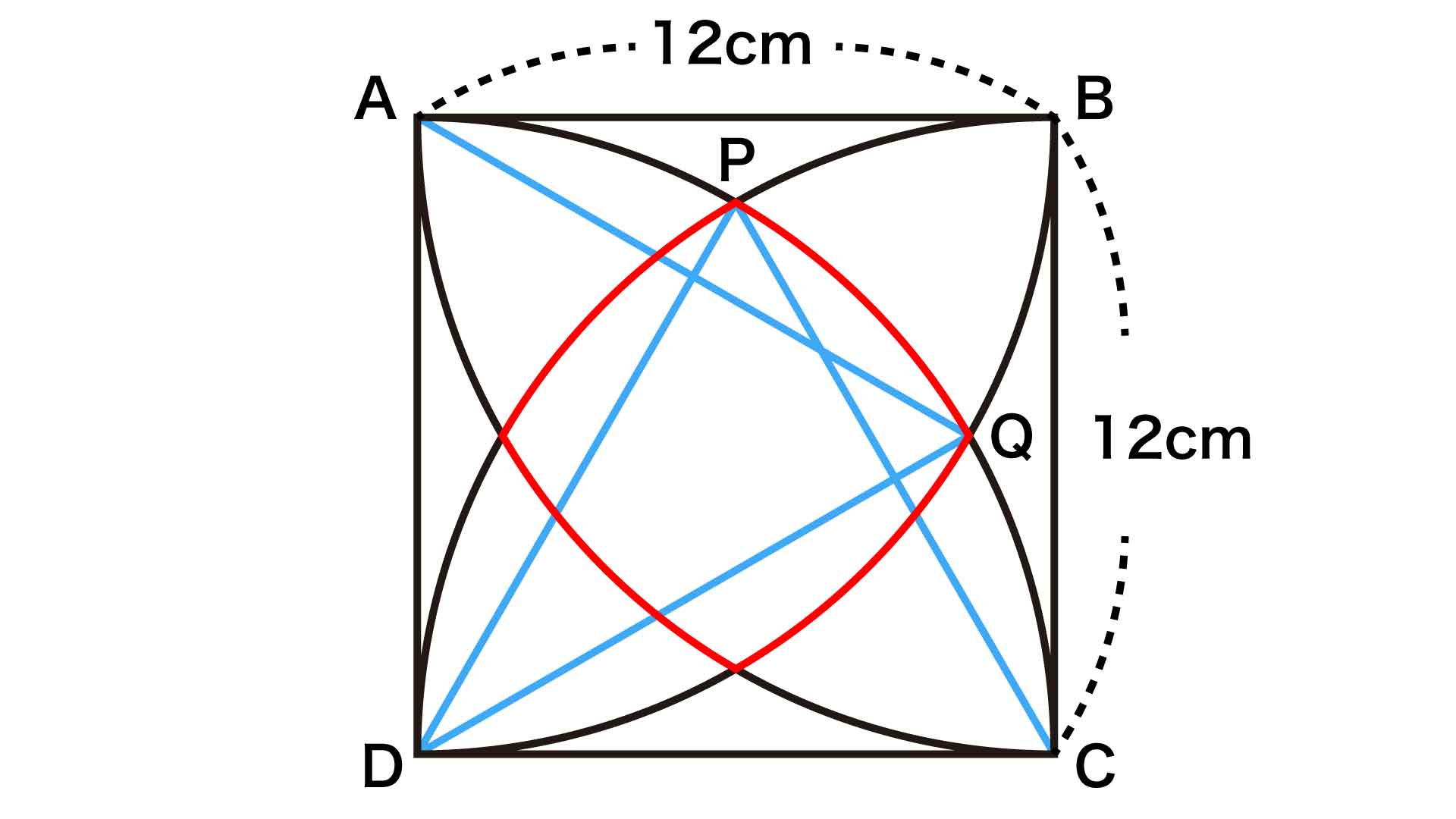このとき、点Aを中心とする扇形に着目すると、ADとAQはどちらも扇型の半径であるため、長さが等しくなります。すなわち、AD=AQです。
同様にして、点Dを中心とする扇形ではDA=DP=DQ=DCです。さらに、点Cを中心とする扇形では、CD=CPです。
以上より、AQ、AD、DP、DQ、DC、CPの長さは、すべて等しく12cmであることがわかります。
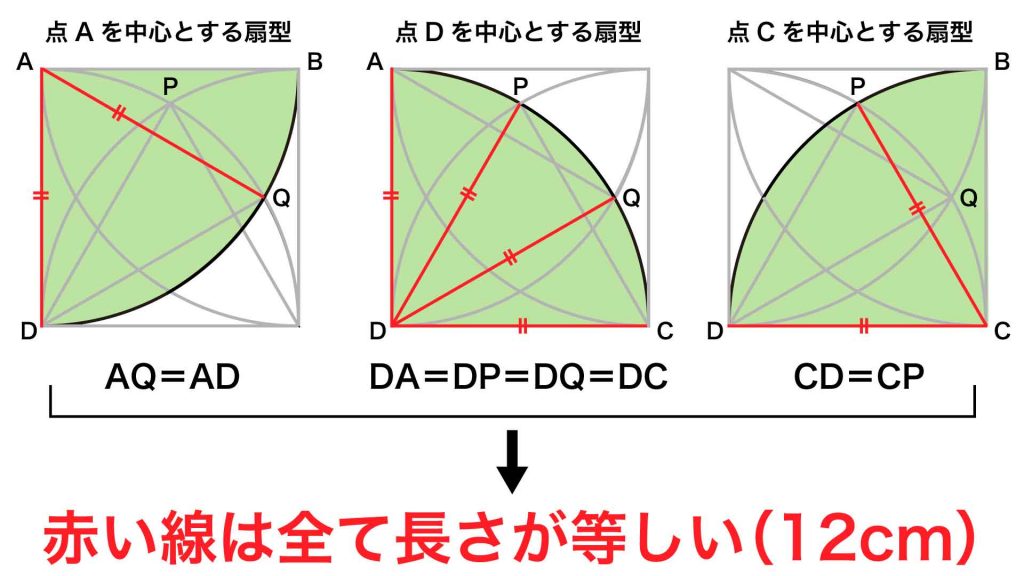
さらに、CD=CP=DP、AD=AQ=DQであることから、三角形CDPと三角形ADQはともに正三角形となります。
弧PQを持つ扇形の中心角の大きさを求める
ここからは、弧PQを弧に持つ扇形の中心角PDQの大きさを求めていきます。
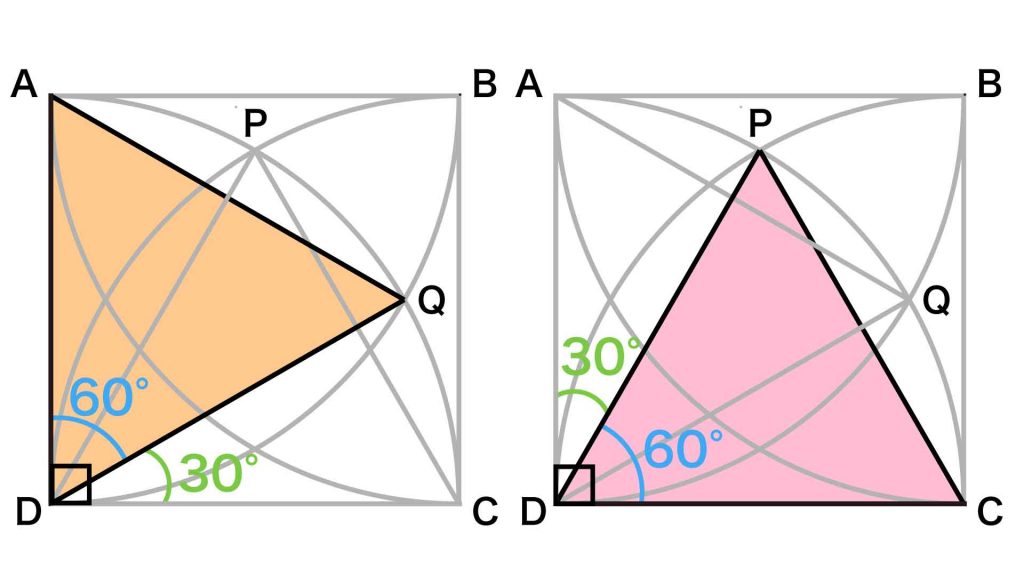
まず、三角形ADQは正三角形なので、角ADQの大きさは60度です。角ADCは90度なので、角QDCの大きさは90-60=30度となります。
同様に、三角形PDCは正三角形なので、角PDCの大きさは60度です。角ADCは90度なので、角ADPの大きさは90-60=30度となります。
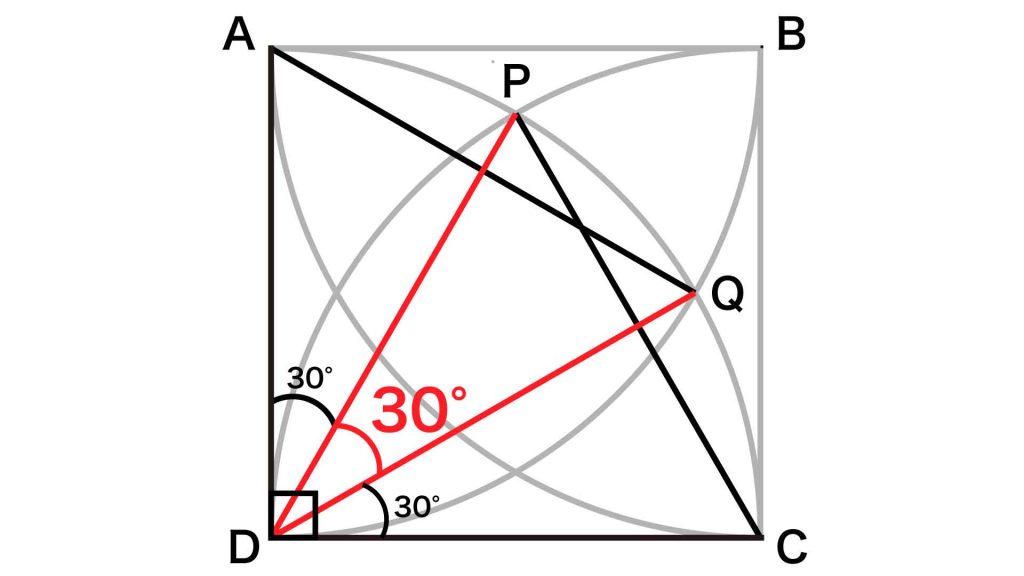
したがって、角PDQの大きさは、角ADC-角QDC-角ADP=90-30-30=30度となります。
弧PQの長さを求める
角PDQの大きさが30度であるので、弧PQの長さは半径12cmの円の円周の360分の30、つまり12分の1にあたります。
したがって、弧ひとつの長さは、12×2×π÷12=2πcmと求められます。
赤い線は弧4つ分
赤い線は、同じ長さの弧が4つ繋がったものでした。
したがって、求める赤い線の長さは、2π×4=8πcmとなります。
答え：8πcm
それではまた次の算数ノートでお会いしましょう！
「ひらめけ！算数ノート」のバックナンバーはこちらから！
【前回の算数ノートはこちら】
【あわせて読みたい】
