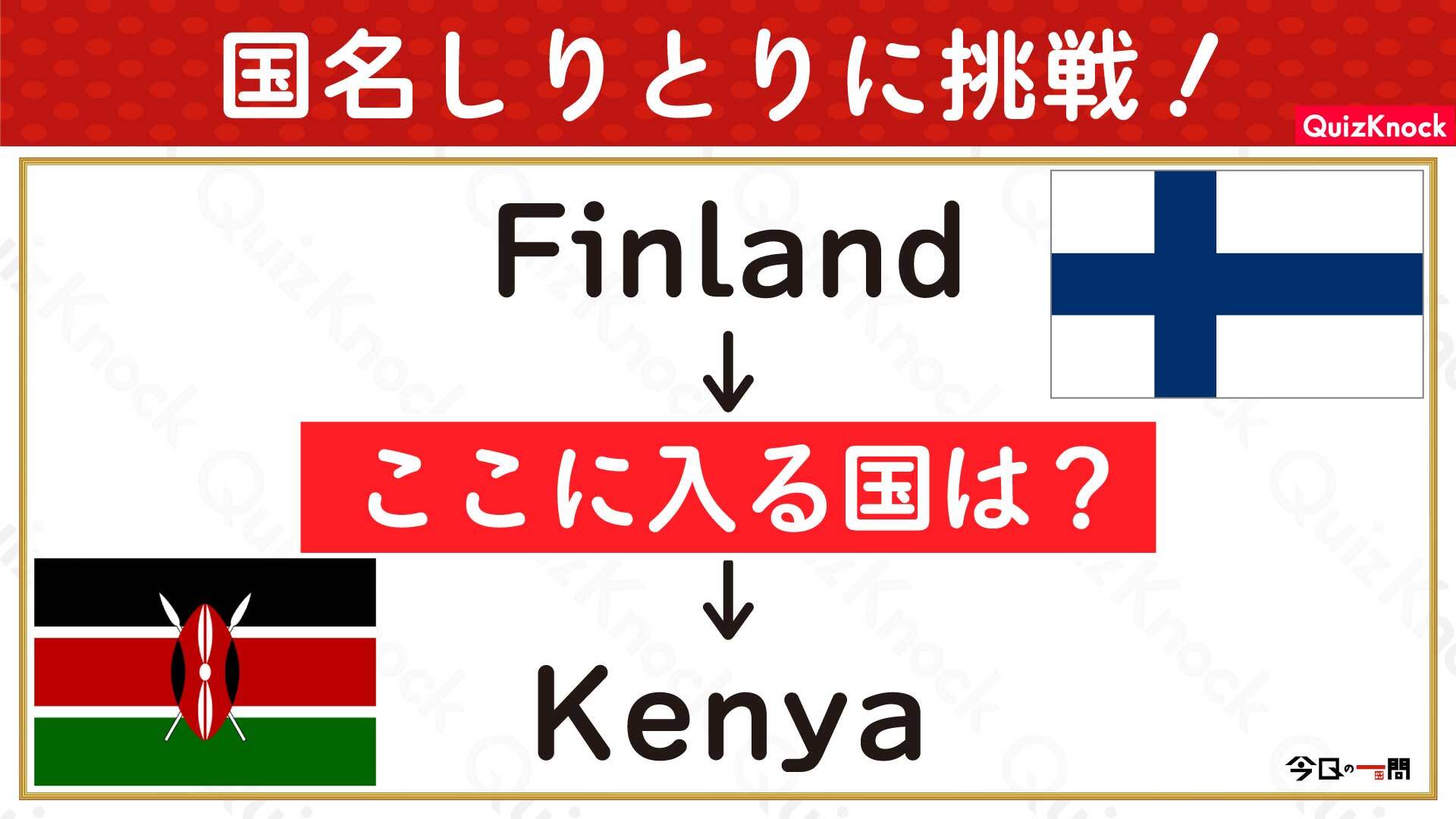
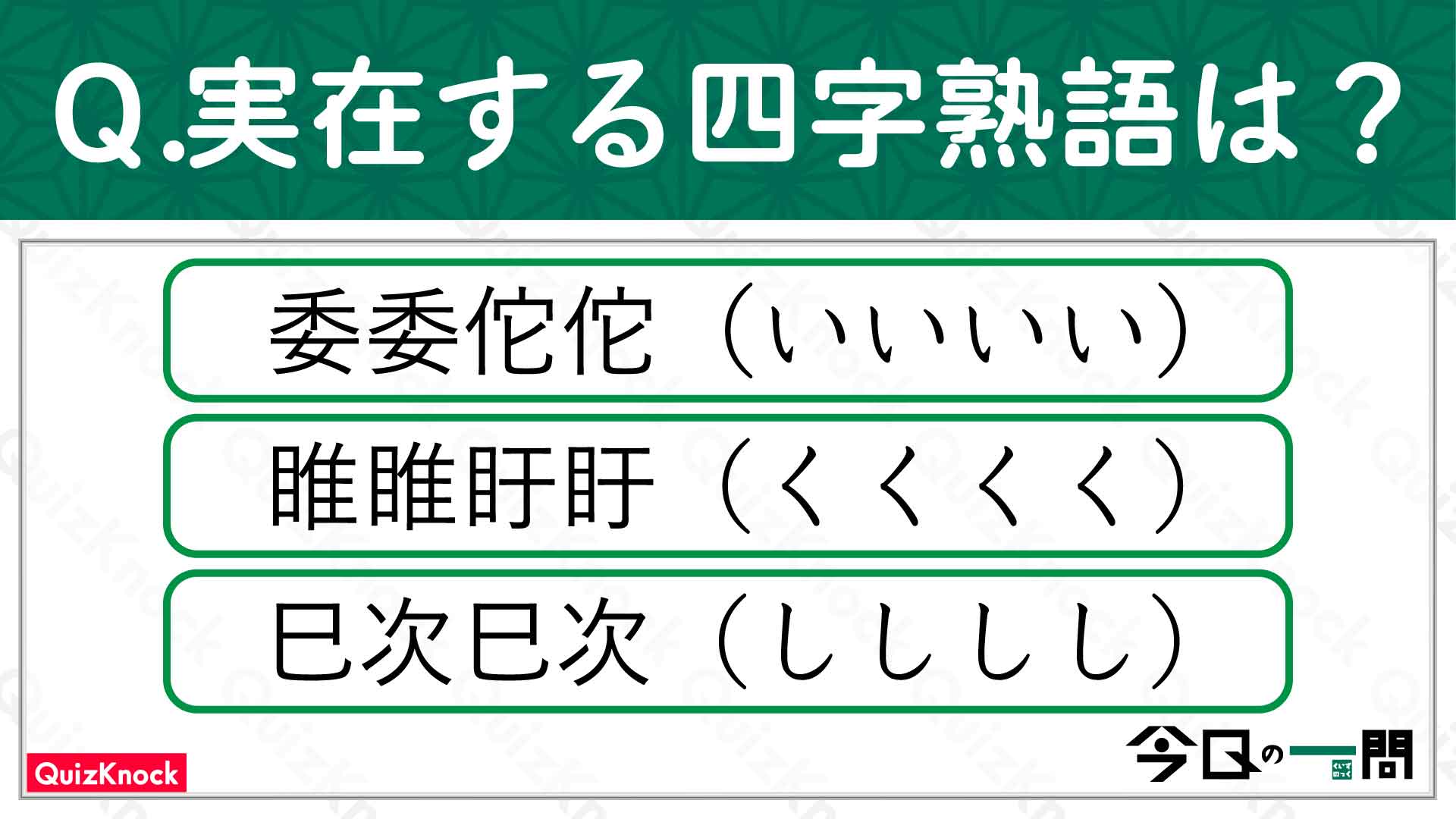
【問題はこちら】
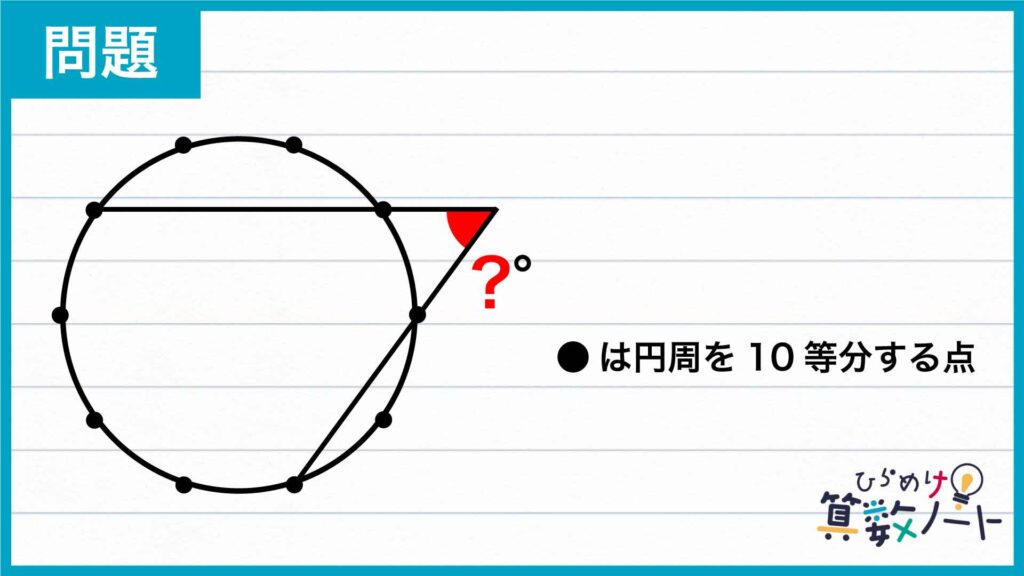
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらです。
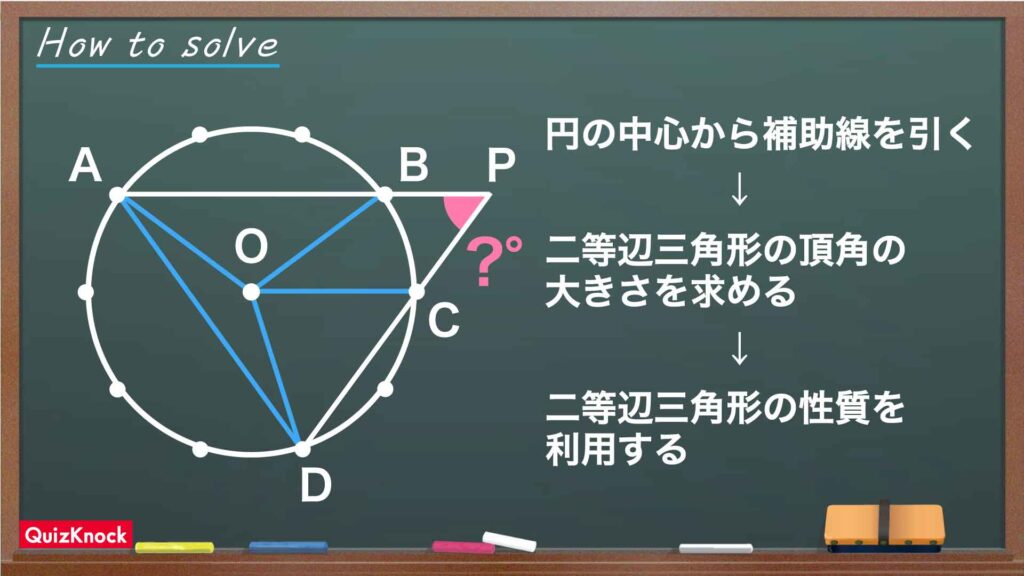
ポイントは、円の中心から補助線を引き、二等辺三角形の性質を利用することです。これを踏まえて解いていきましょう!
円の中心から補助線を引く
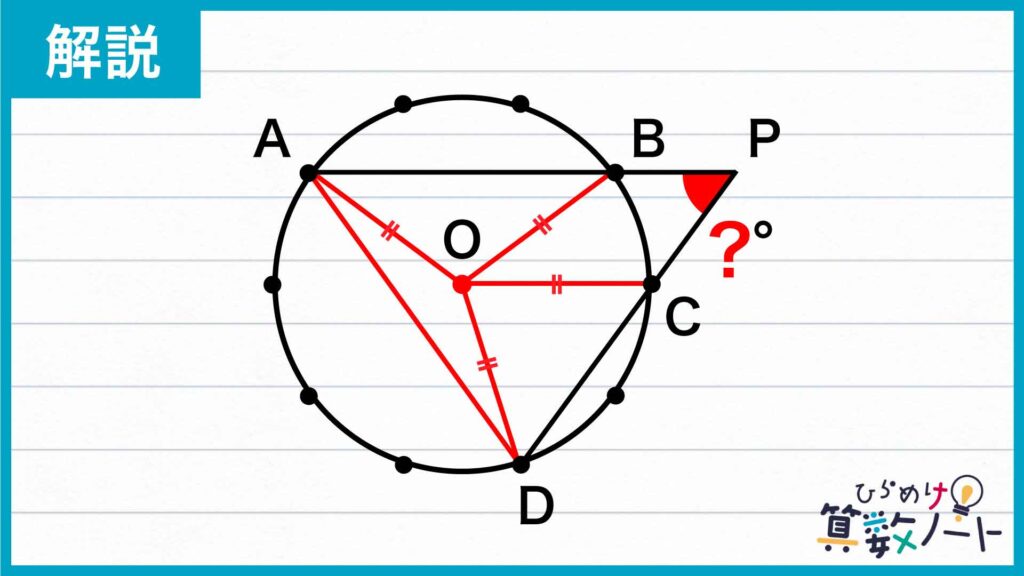
次の図のように各点に記号を振り、補助線を引きます。ここで、点Oは円の中心です。
このとき、点A、B、C、Dはすべて円周上の点なので、線分OA、OB、OC、ODは円の半径であり、長さが等しいです。よって、三角形OBA、OAD、ODCは二等辺三角形であることがわかります。
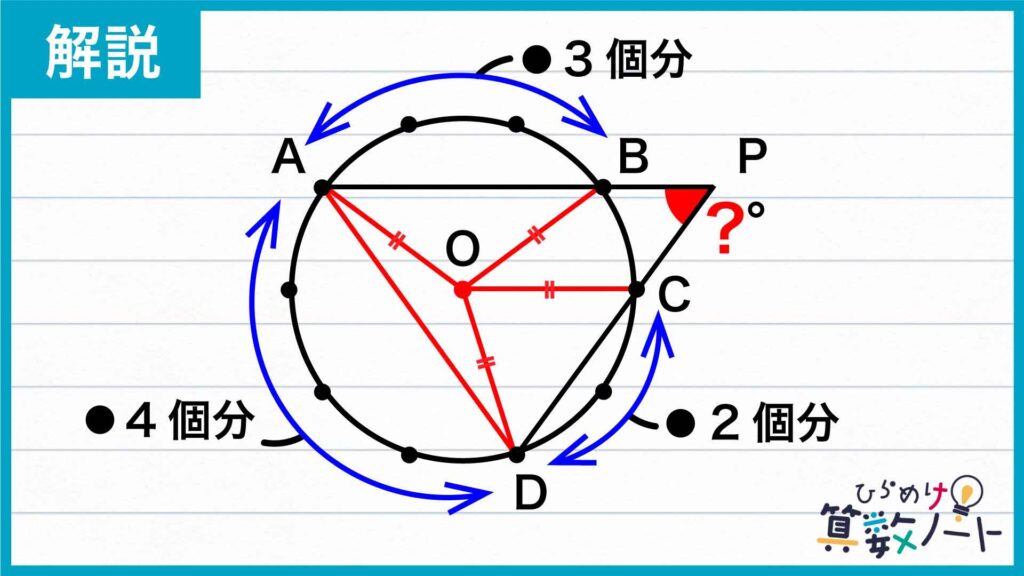
二等辺三角形の頂角の大きさを求める
角BOAの大きさについて考えます。円周上の点は円周を10等分しているため、隣り合う2つの点を弧とする扇形の中心角の大きさは、360÷10=36度となります。点Aから点Bまでは点3個分離れているので、角BOAの大きさは36×3=108度と求めることができます。
同様にして、点Aから点Dまでは点4個分、点Dから点Cまでは点2個分離れているので、角AODの大きさは36×4=144度、角DOCの大きさは36×2=72度となります。
角APDの大きさを求める
三角形AOBは、頂角が108度の二等辺三角形なので、角BAOの大きさは、(180-108)÷2=36度です。同様にして、角OADと角ADOの大きさは、(180-144)÷2=18度、角ODCの大きさは、(180-72)÷2=54度と求めることができます。
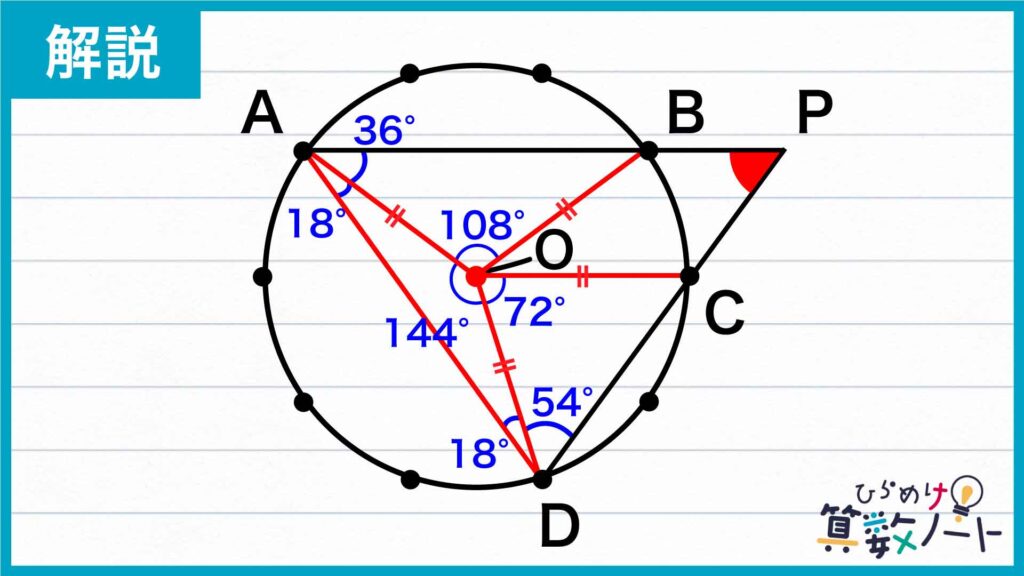
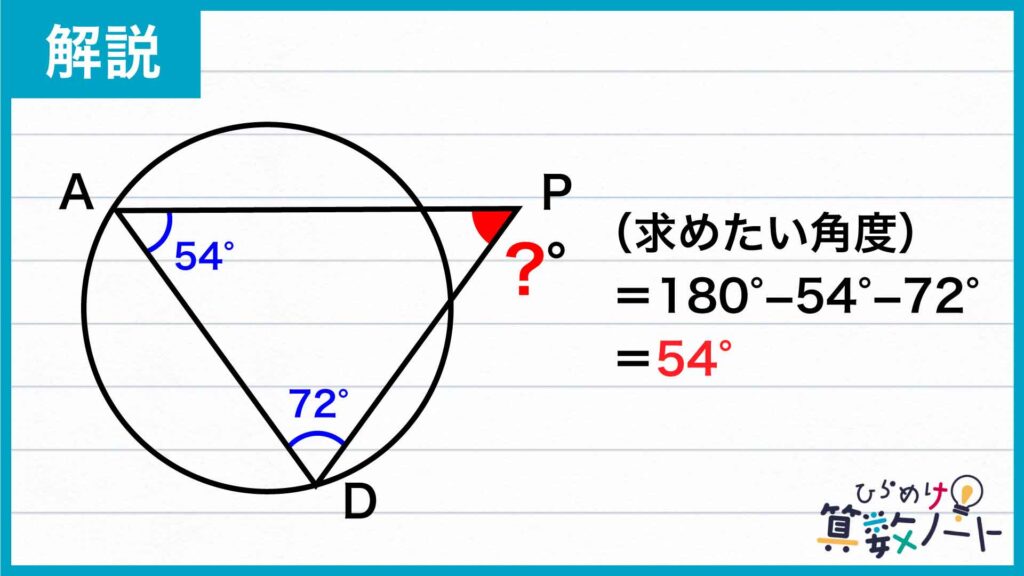
三角形PADに注目すると、角PADの大きさは36+18=54度、角ADPの大きさは18+54=72度なので、角DPAの大きさは180-54-72=54度です。
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】