中学受験レベル！「図形の面積」を求める問題、あなたは解けますか？

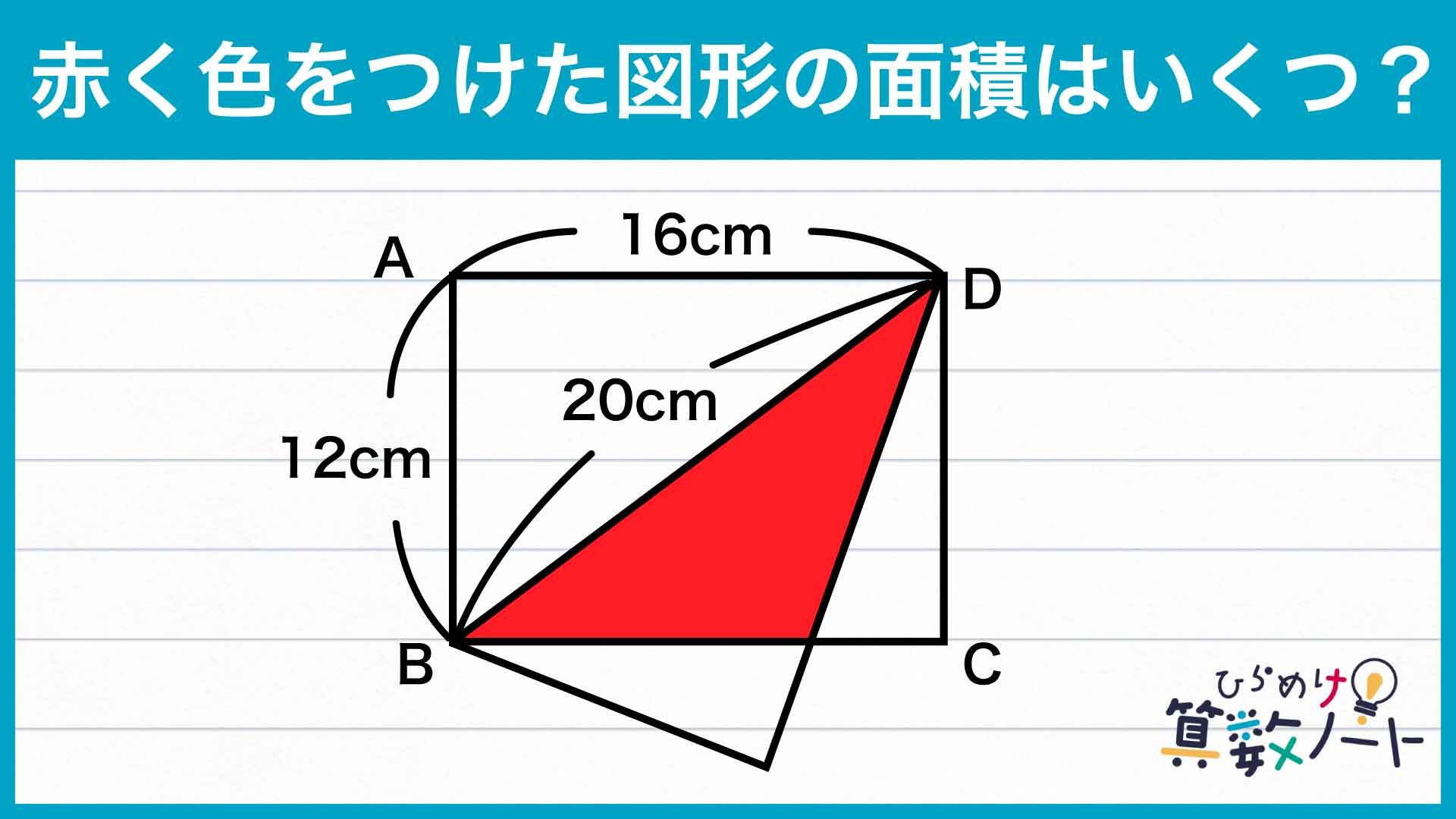
【問題はこちら】

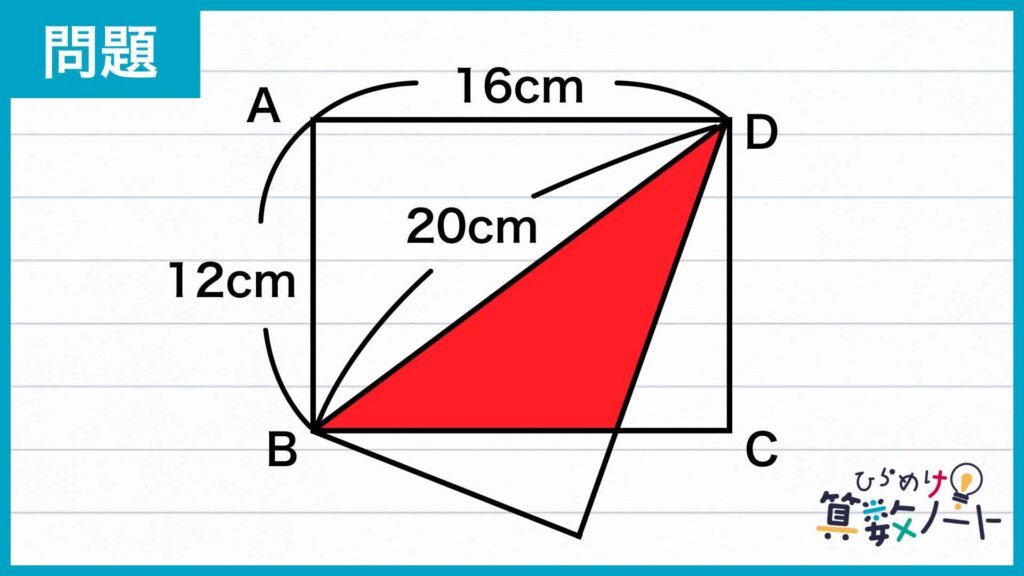
1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題の解き方をまとめた図がこちらです。

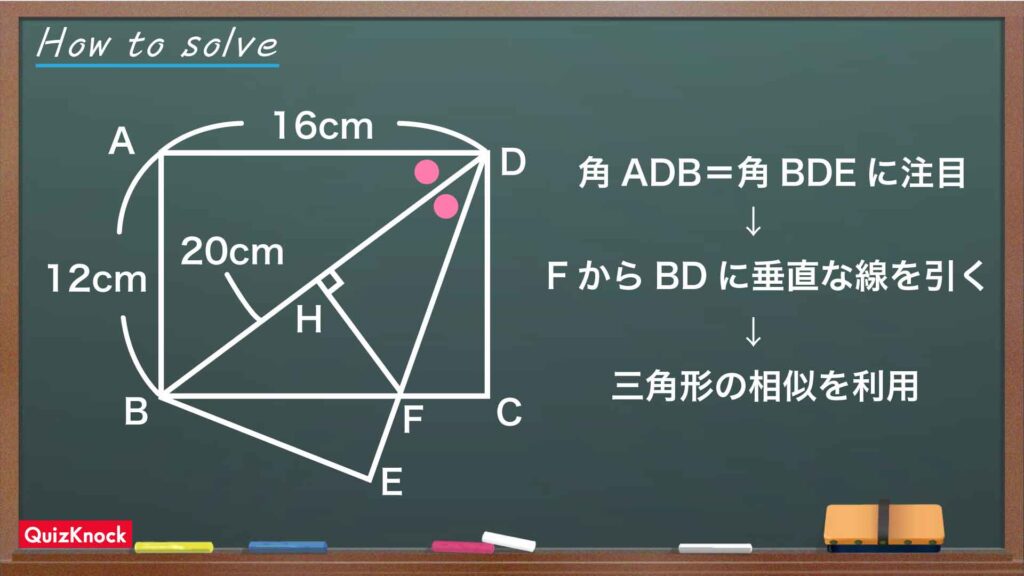
ポイントは、補助線を引いて、三角形の相似に着目することです。これを踏まえて解いていきましょう！

折り返しの性質に注目する

次の図のように点Eを振ります。

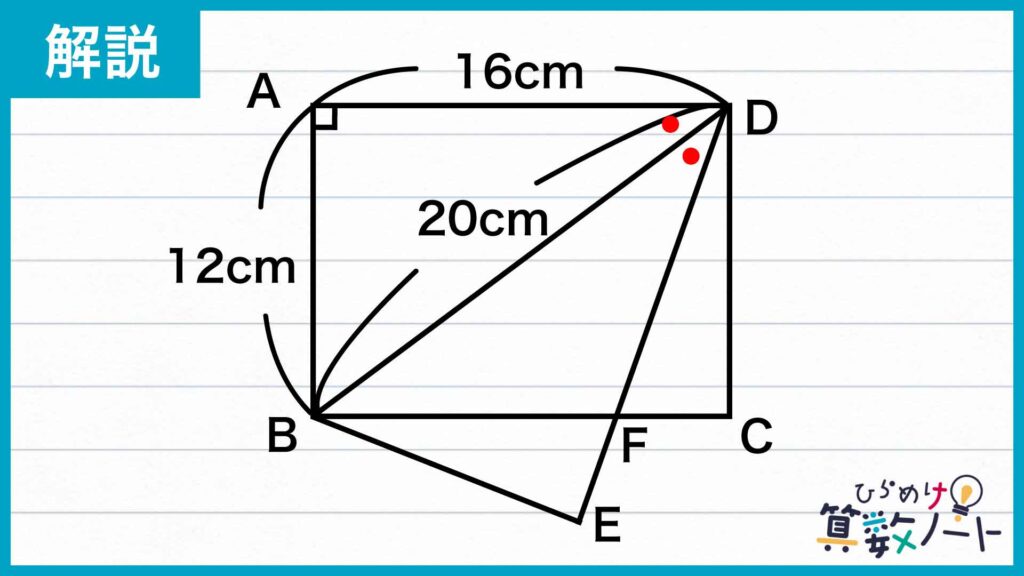
このとき、三角形ADBは、四角形ABCDの折り返しによって三角形EDBに移るため、角ADB=角EDBとなります（ポイント①）。

三角形の相似を見つける

次の図のように、辺BCと辺DEの交点を点Fとします。そして、点Fから辺BDに引いた垂線の足を点Hとします。辺BDを底辺とみると、三角形DBFの面積を求めるには高さにあたる辺HFの長さが必要です。

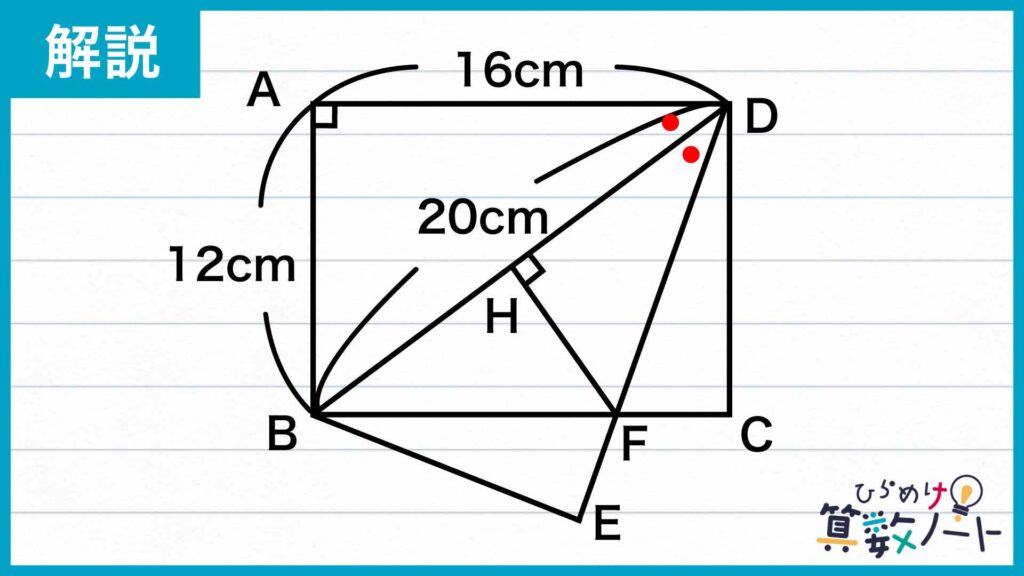
三角形DABと三角形DHFに注目します。四角形ABCDは長方形なので、角DAB=90度であり、角DAB=角DHFとなります。さらに、角BDA=角FDHです（ポイント①より）。よって、対応する2組の角の大きさがそれぞれ等しいことから、三角形DABと三角形DHFは相似の関係にあります（ポイント②）。

二等辺三角形の性質を利用する

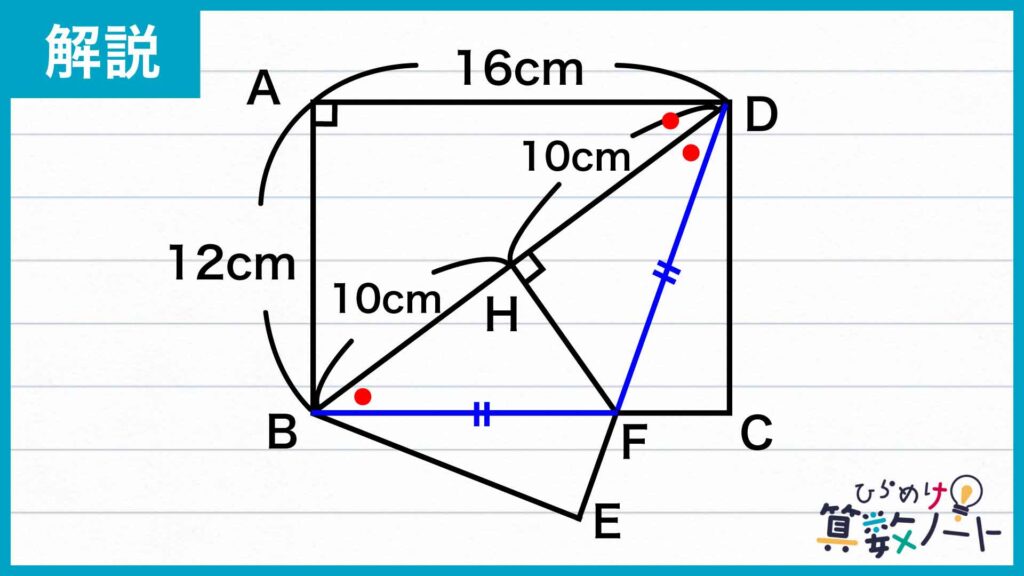
四角形ABCDは長方形なので、辺ADと辺BCは平行です。よって、平行線についての錯角の関係から、角ADB=角DBFとなります。さらに、角ADB=角BDFなので、角BDF=角DBFです。このことから、三角形FDBは二等辺三角形であることがわかります。

二等辺三角形は、頂角（長さの等しい辺の間の角）から底辺に降ろした垂線に関して線対称です。よって、線分DHの長さは、辺DBの長さの半分の10cmとなります（ポイント③）。

辺の長さの比を用いて面積を求める

ポイント②で示したように、三角形DABと三角形DHFは相似の関係にあるため、対応する辺の長さの比が等しいです。

三角形DABにおいて、辺DA=16cm、辺AB=12cm、辺BD=20cmです。辺DHと辺HFの長さの比は、16cm:12cm=4:3なので、ポイント③から辺DH=10cmであることから、辺HF=10×(3/4)=7.5cmであることがわかります。

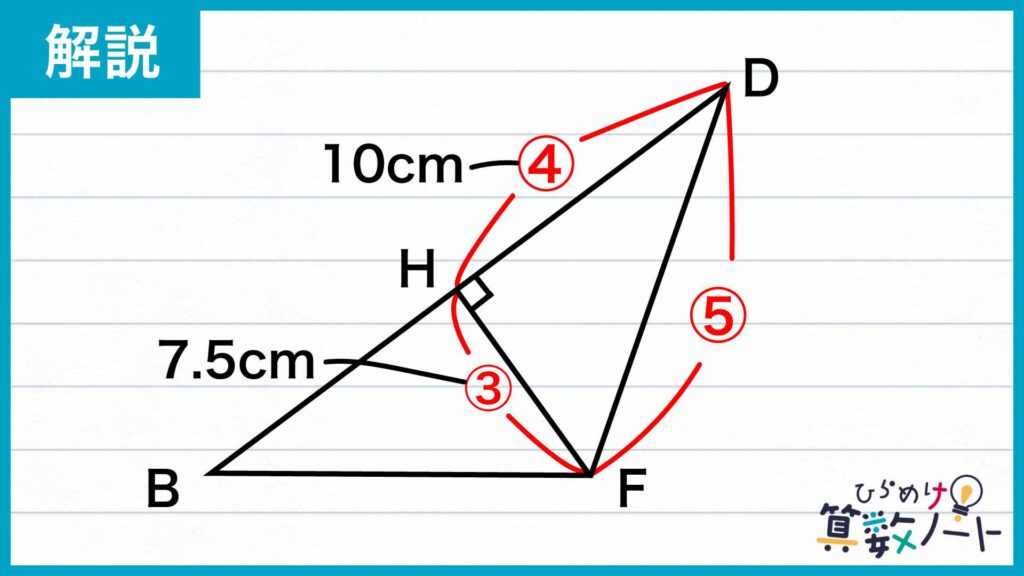
よって三角形DBFの面積は、20×7.5÷2=75cm²です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】