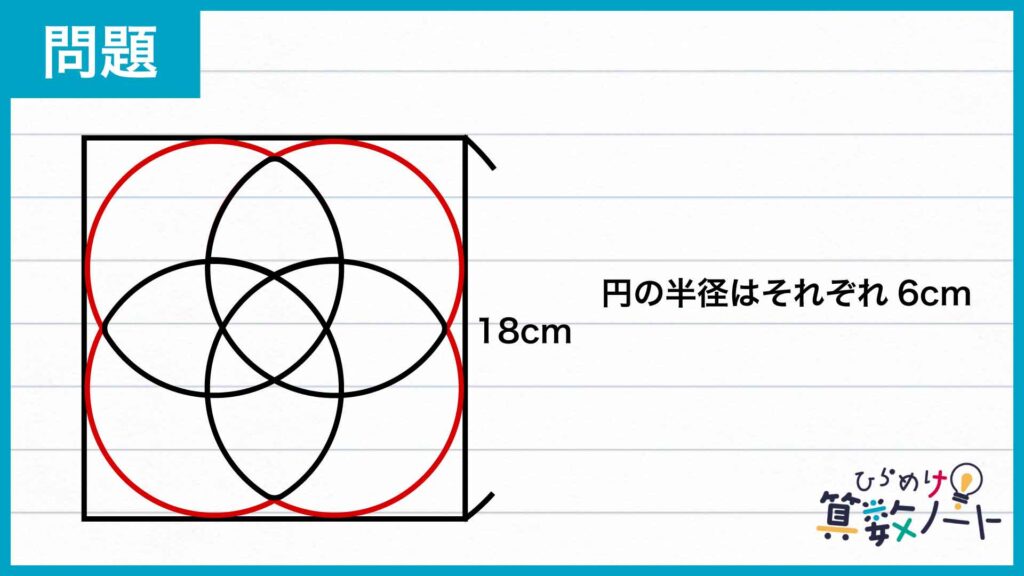
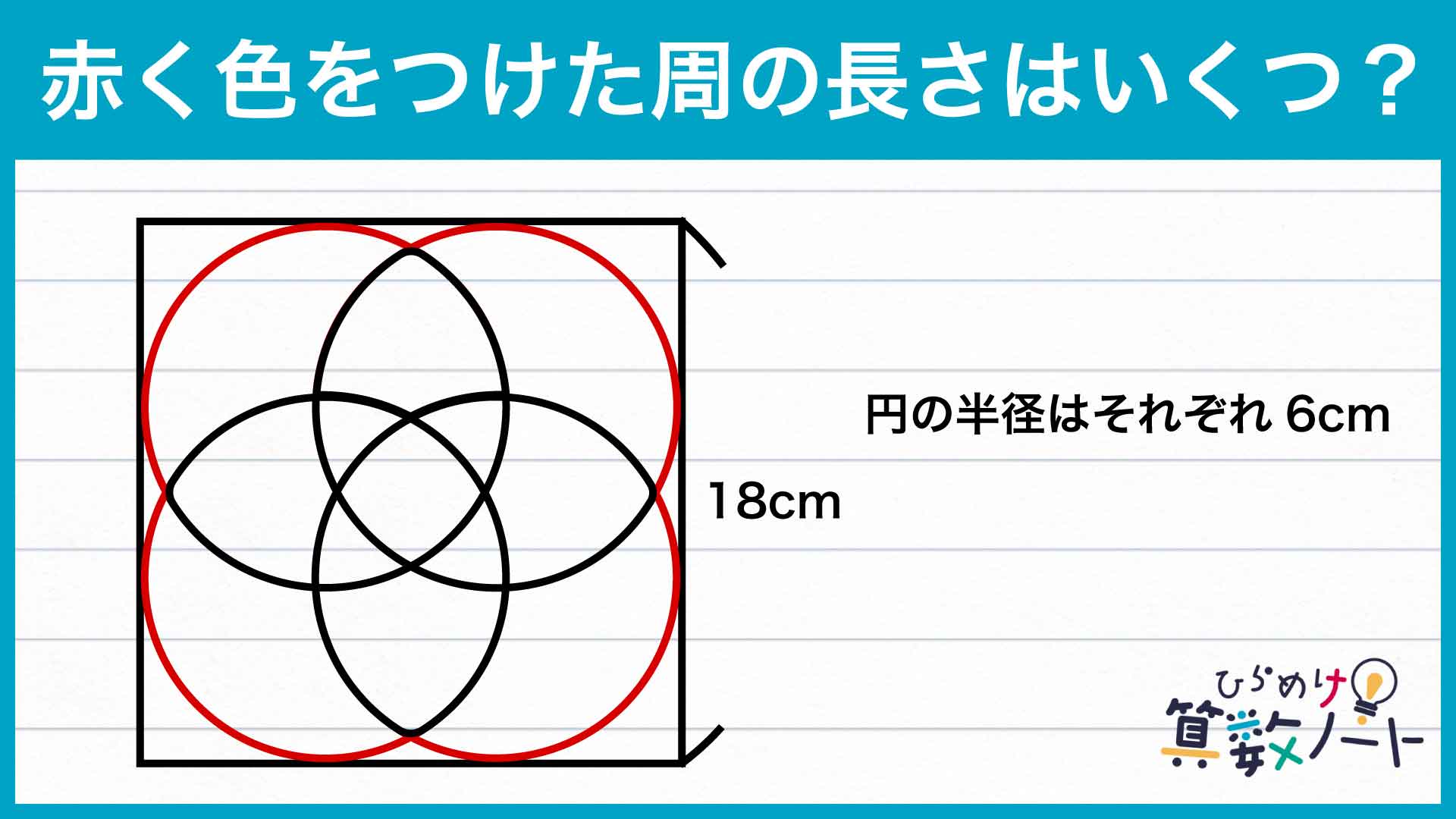
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ!以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつをご紹介します。
今回の問題の解き方をまとめた図がこちらになります。
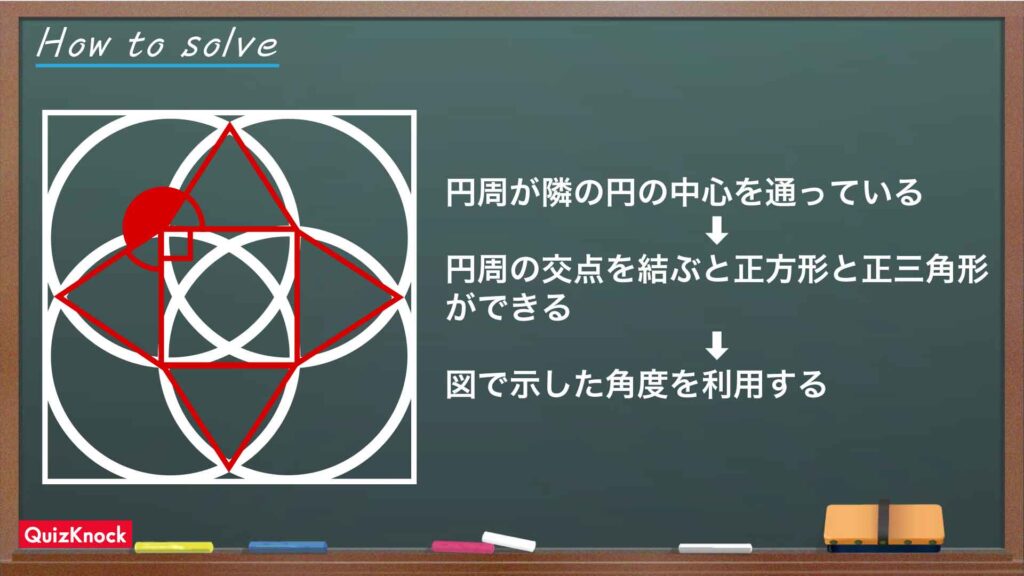
ポイントは、円周の交点を結ぶ補助線を引いて、正方形や正三角形など角度が求めやすい図形に着目することです。これを踏まえて解いていきましょう!
扇形の弧の角度を求める
最終的に求めたい図形の周囲の長さは、下の図で示した扇形の弧ABの長さの4つ分です。
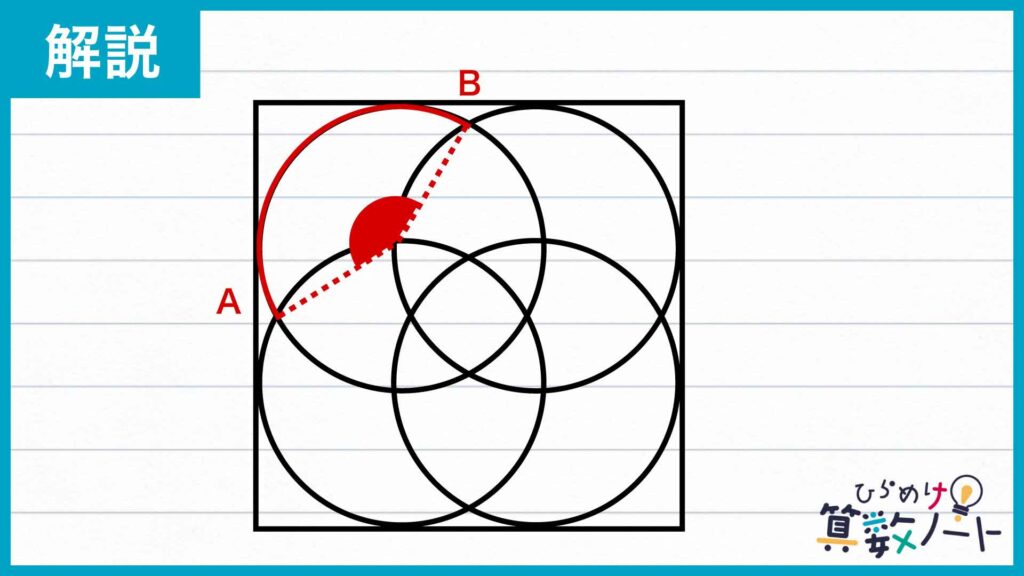
扇形の弧ABの長さを求めるには弧ABに対する中心角を求める必要があります。どのようにすれば中心角を求めることができるでしょうか?
円周の交点が隣の円の中心を通っていることに注目する
1辺が18cmの正方形に半径が6cmの円が並んでいることから、重なった円の円周は縦・横隣の円の中心を通っていることがわかります。
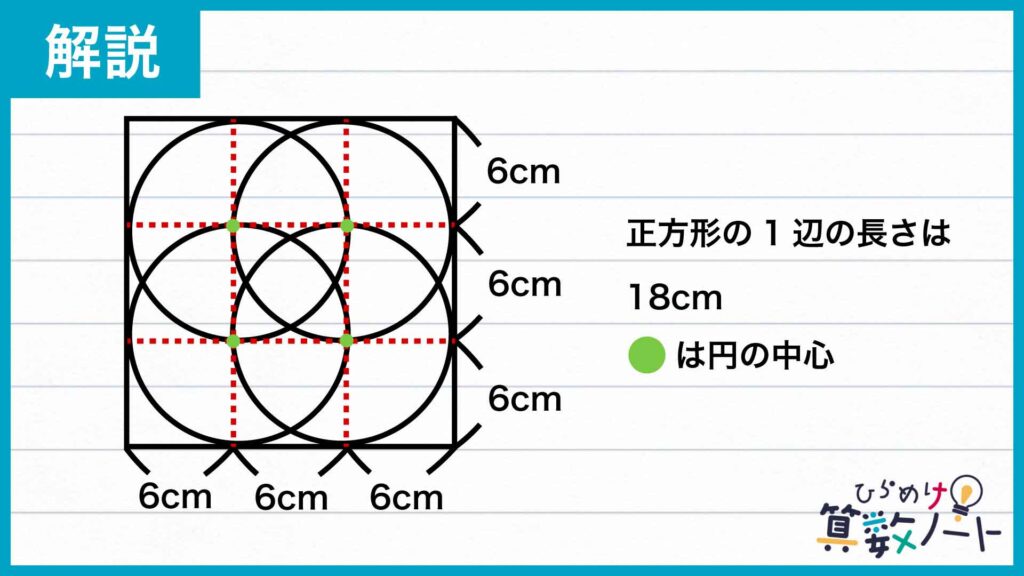
ここで下の図のように円周の交点を結ぶと、四角形と三角形ができます。四角形を構成する補助線は外側の正方形の各辺に平行であり、また1辺がすべて6cmであるため正方形です。三角形はすべての辺が半径6cmの円の半径であるため、正三角形になります。
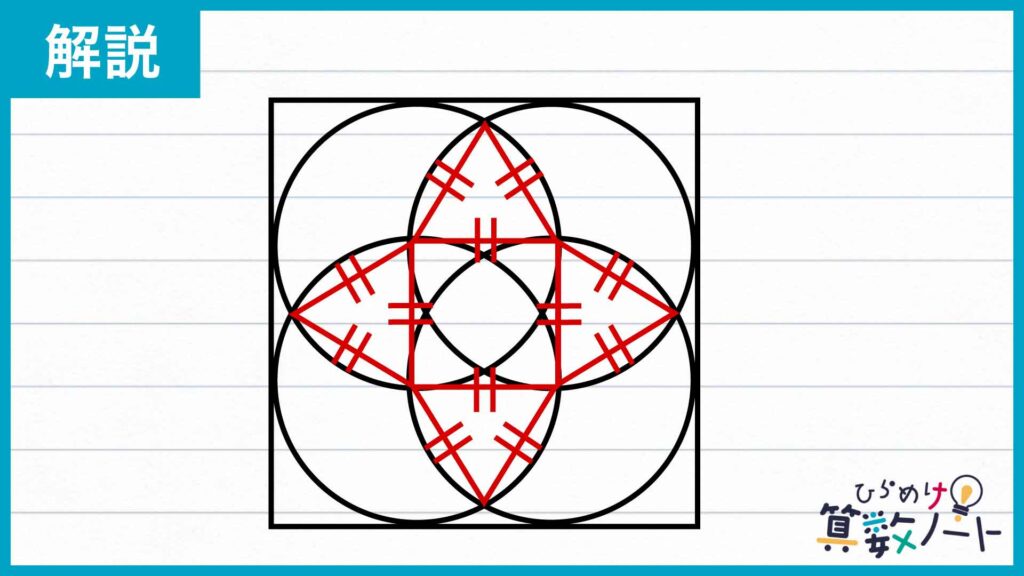
外側の角が求まるから……
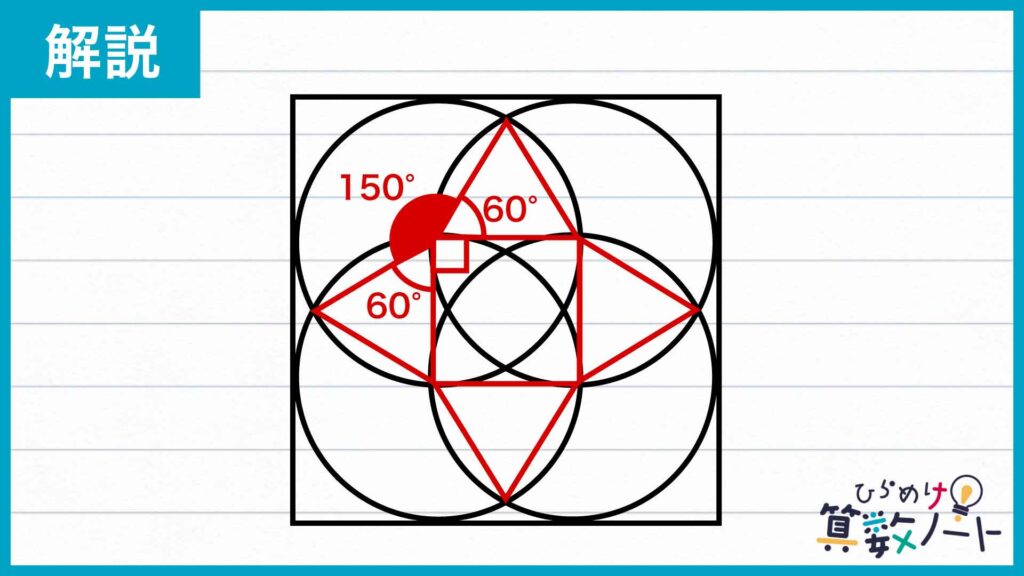
弧ABの中心角は、補助線を引いてできた正方形と2つの正三角形を利用して求めると、360-(60×2+90)=150°になります。したがって、弧ABの長さは12π×(150/360)=5π cmです。
求める図形の周囲の長さは弧ABの長さの4つ分だったので、答えは5π×4=20π cmとなります。
答え:20πcmそれではまた次の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







