小学5年生で解ける「図形の面積」を求める問題にチャレンジ！

【問題はこちら】

1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題の解き方をまとめた図がこちらです。

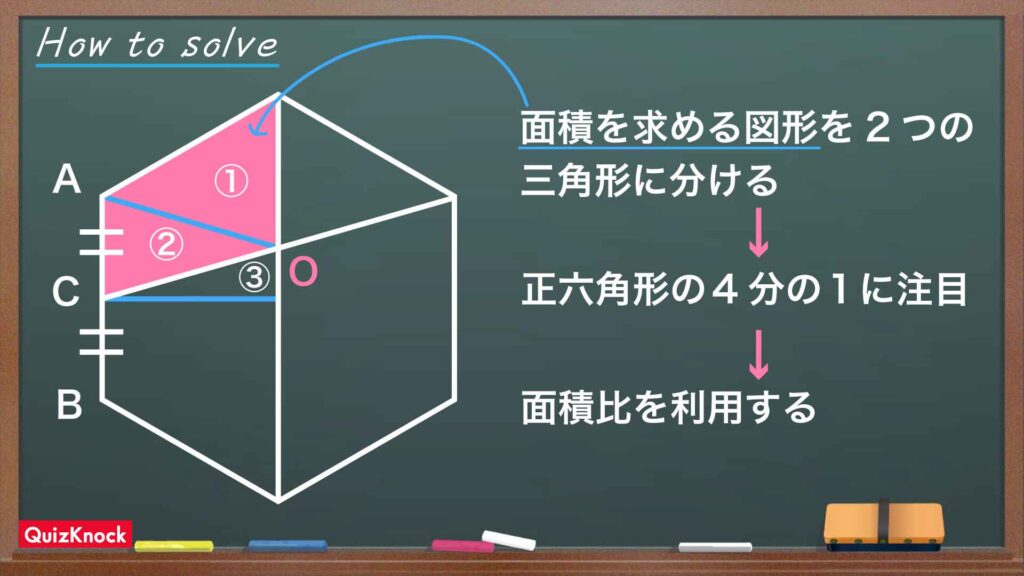
ポイントは、四角形を三角形に分けて面積比を利用することです。これを踏まえて解いていきましょう！

四角形を2つの三角形に分ける

図のように点D、点Eをふります。このとき、面積を求める図形は四角形ACDEです。そして、線分ADを引いて四角形ACDEを三角形ACDと三角形ADEに分けます。

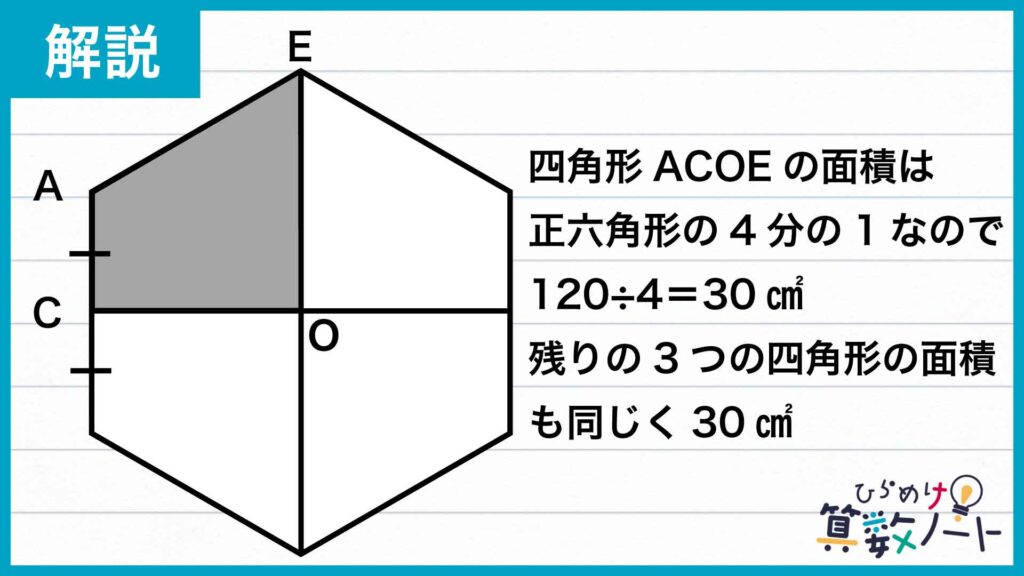
点Cと正六角形の中心を結ぶ

次に、図のように正六角形の中心を点Oとして、線分COを引きます。こうしてできた四角形ACOEは正六角形を4等分した図形で、面積は120÷4=30cm²です。

さらに、三角形COD、三角形ACD、三角形ADEに注目します。それぞれ辺OD、辺AC、辺DEを底辺とみると高さが同じなので、この3つの三角形の面積比は、辺OD、辺AC、辺DEの長さの比と等しいです。

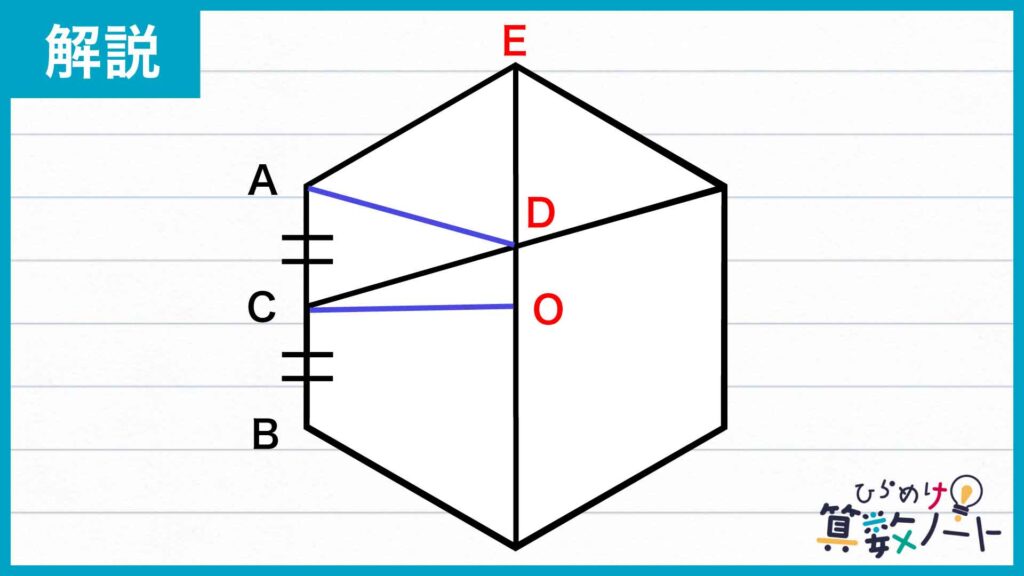
3つの三角形の面積比を考える

図のように点F、点Gをふり、線分DOの長さを①とします。このとき、CO=OFより三角形CODと三角形CFGの相似比は1:2なので、線分GFの長さは②となります。GF=ACより線分ACの長さも②です。点Cは線分ABの中点なので線分ABの長さは④です。この図形は正六角形なのでAB=EOであることから、線分EOの長さも④、線分EDの長さは④-①=③となります。

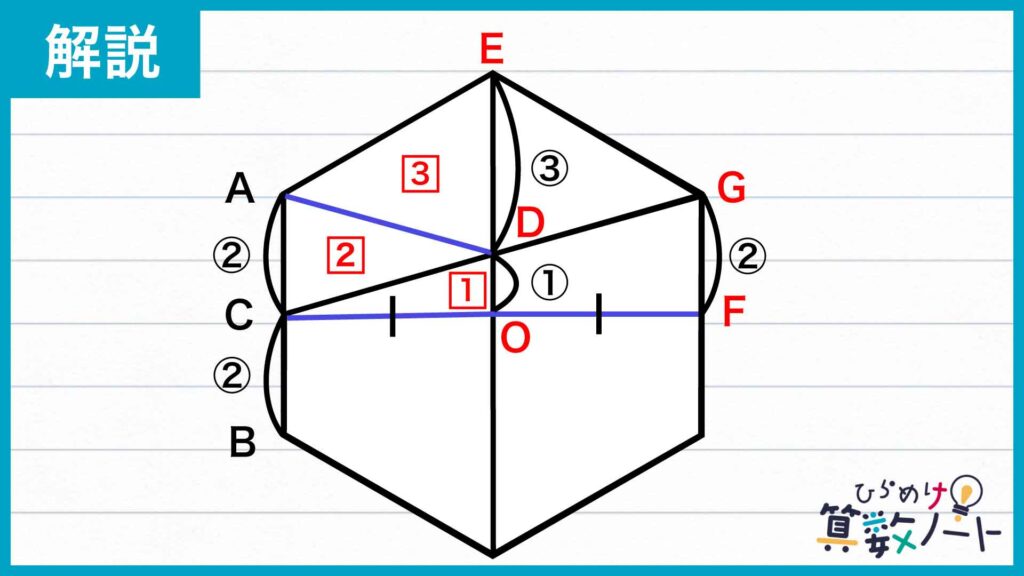
これにより、三角形CODと三角形ACDと三角形ADEの面積比は1:2:3であることがわかります。

面積を求める

四角形ACOEの面積は30cm²なので、四角形ACDEの面積は30÷(1+2+3)×5=25cm²です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】