問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
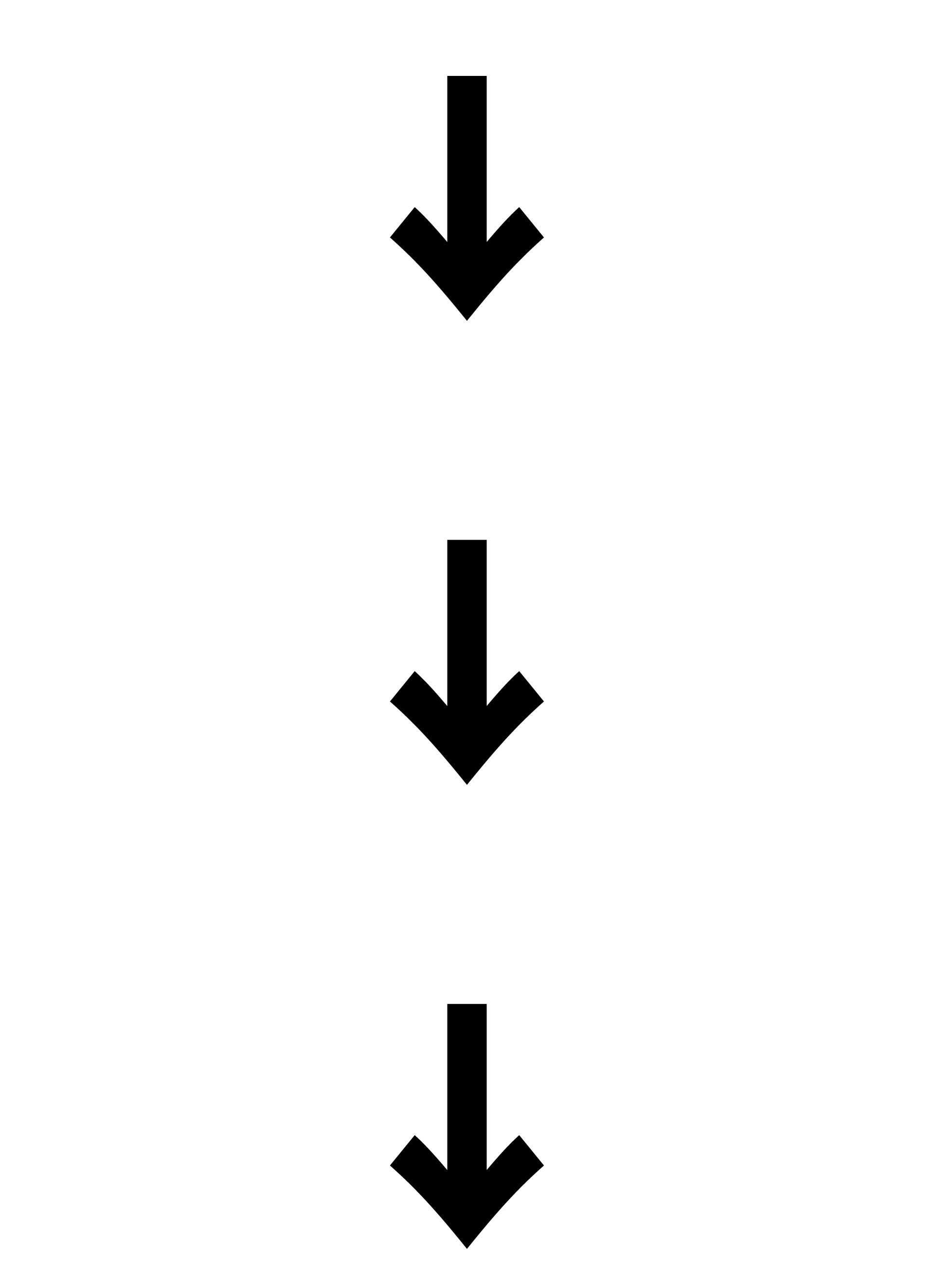
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
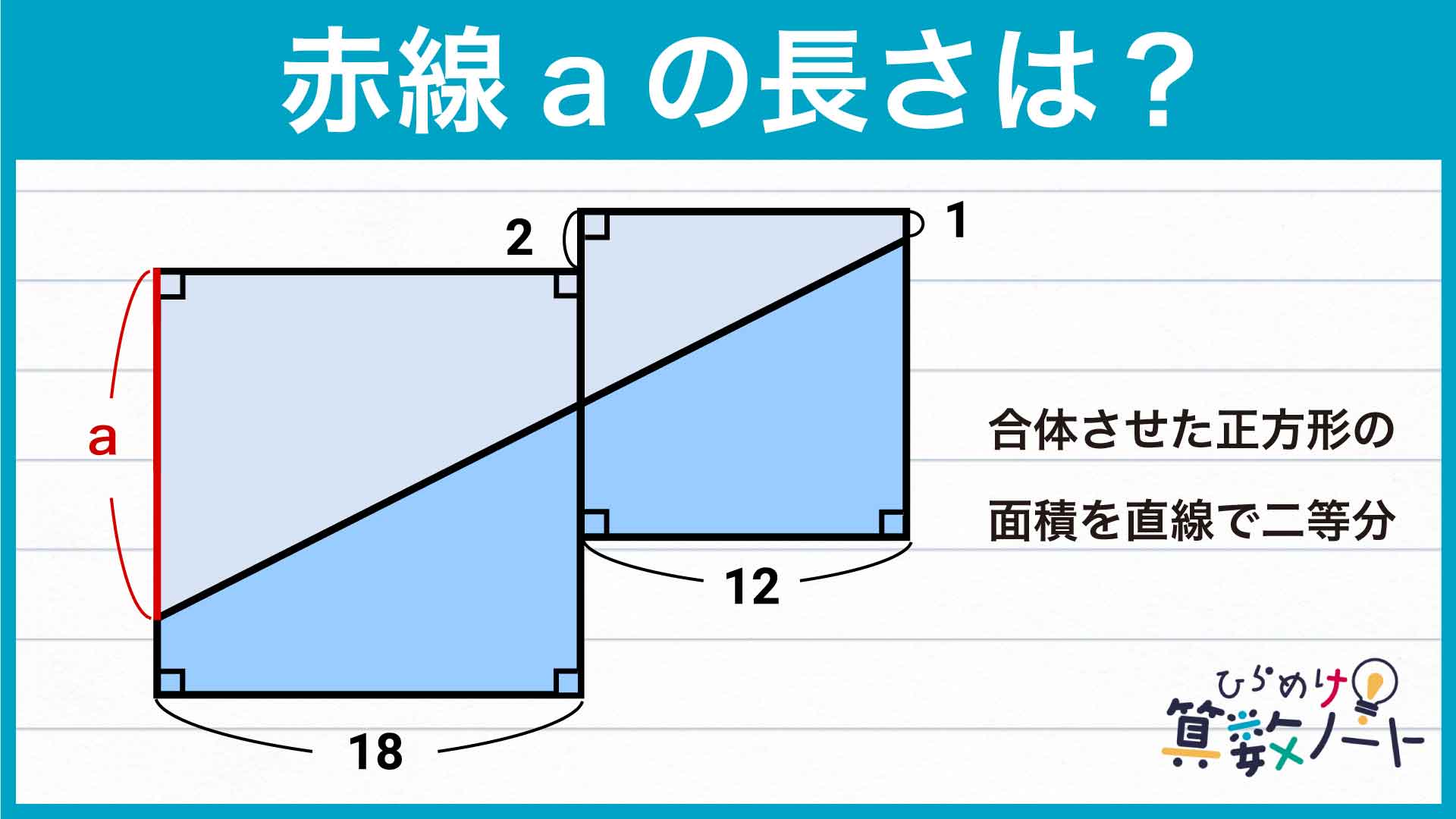
この問題の解き方をまとめた図がこちらです。
ポイントは、デコボコの図形に長方形を書き足し、考えやすい台形を作ることです。
では、このポイントを踏まえつつ解いていきましょう!
長方形を書き足す
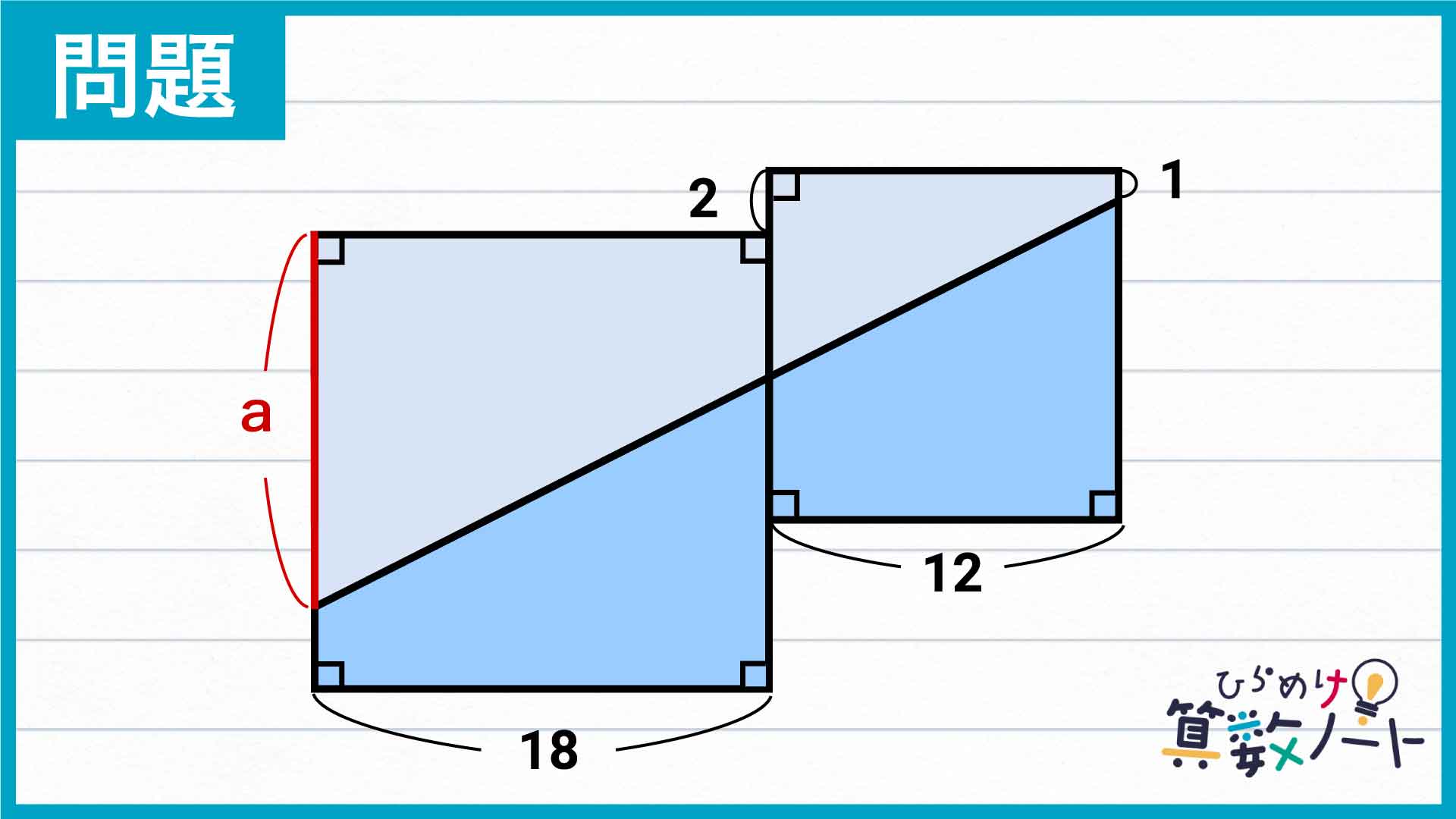
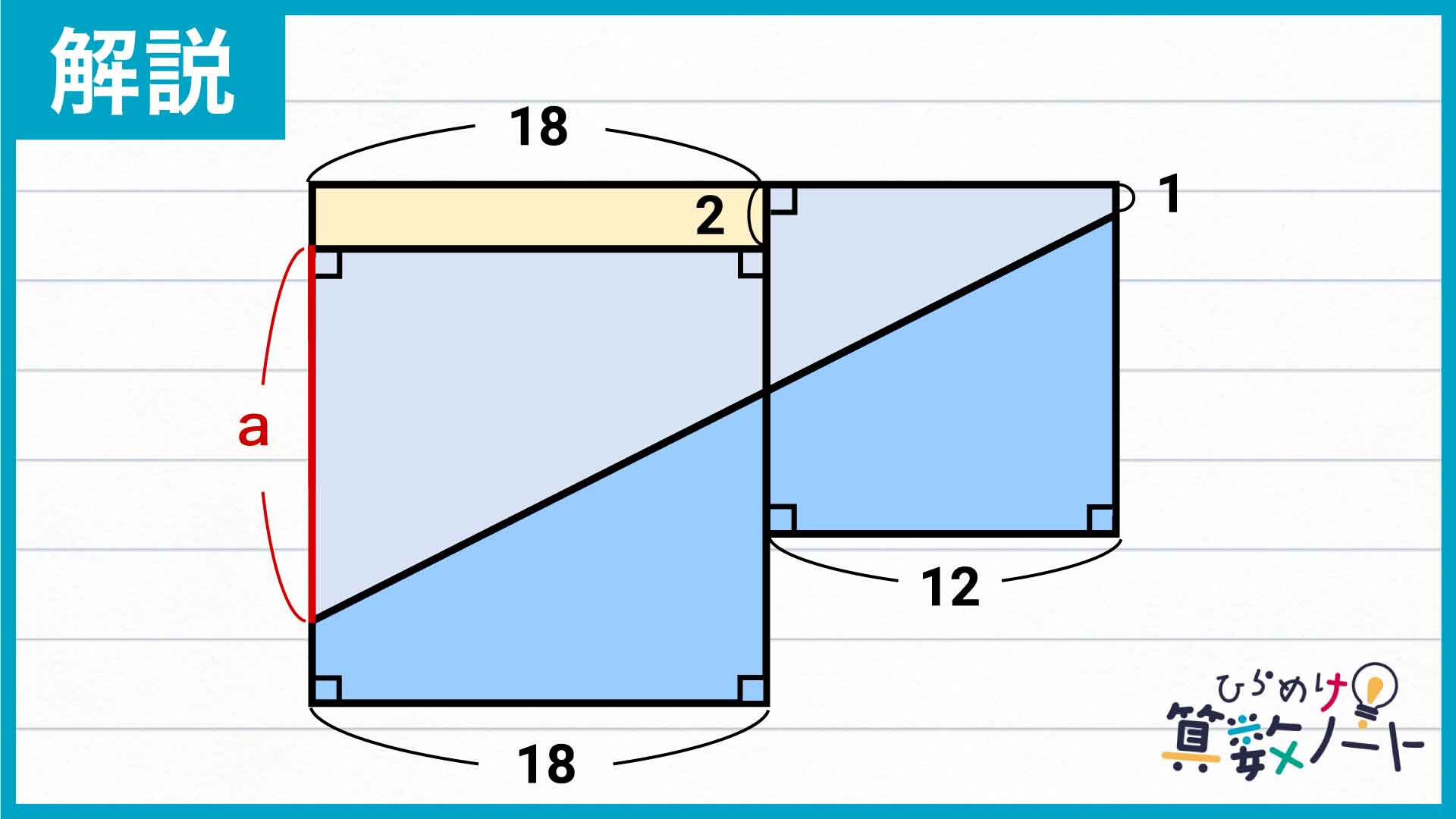
合体した正方形の面積を二等分すると、台形が2つ組み合わさったようなデコボコの図形が出来上がってしまいます。このままでは長さや面積の計算がしづらいため、空白の部分を埋めるようにして長方形を書き足してみます。
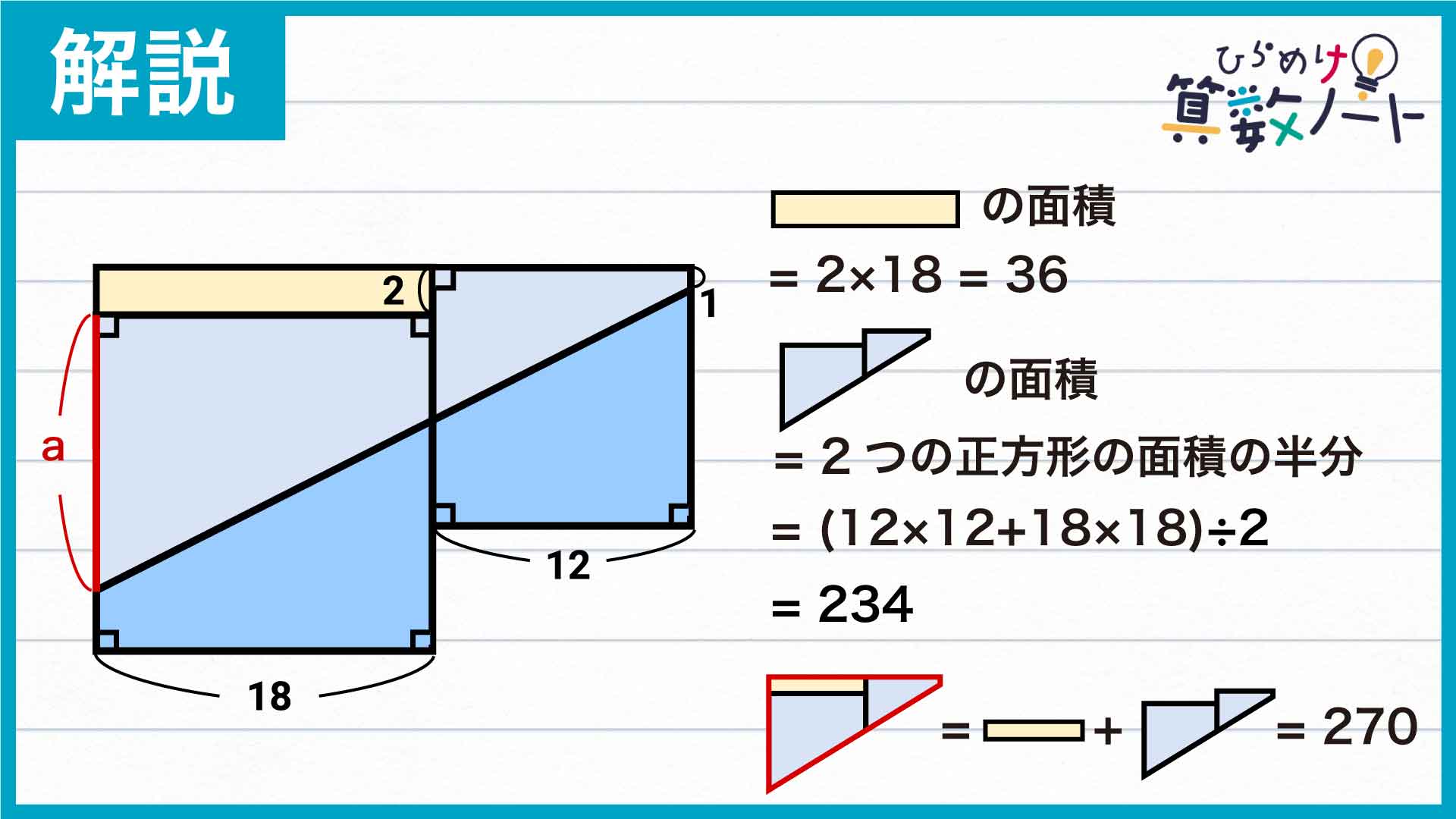
長方形を書き足すことで、図の上部分に大きな台形が現れました。書き足した長方形の面積は2×18=36です。また、台形の残りの部分は合体した正方形の面積を二等分したものなので、その面積は(18×18+12×12)÷2=234です。よって、台形の面積は36+234=270であるとわかります。
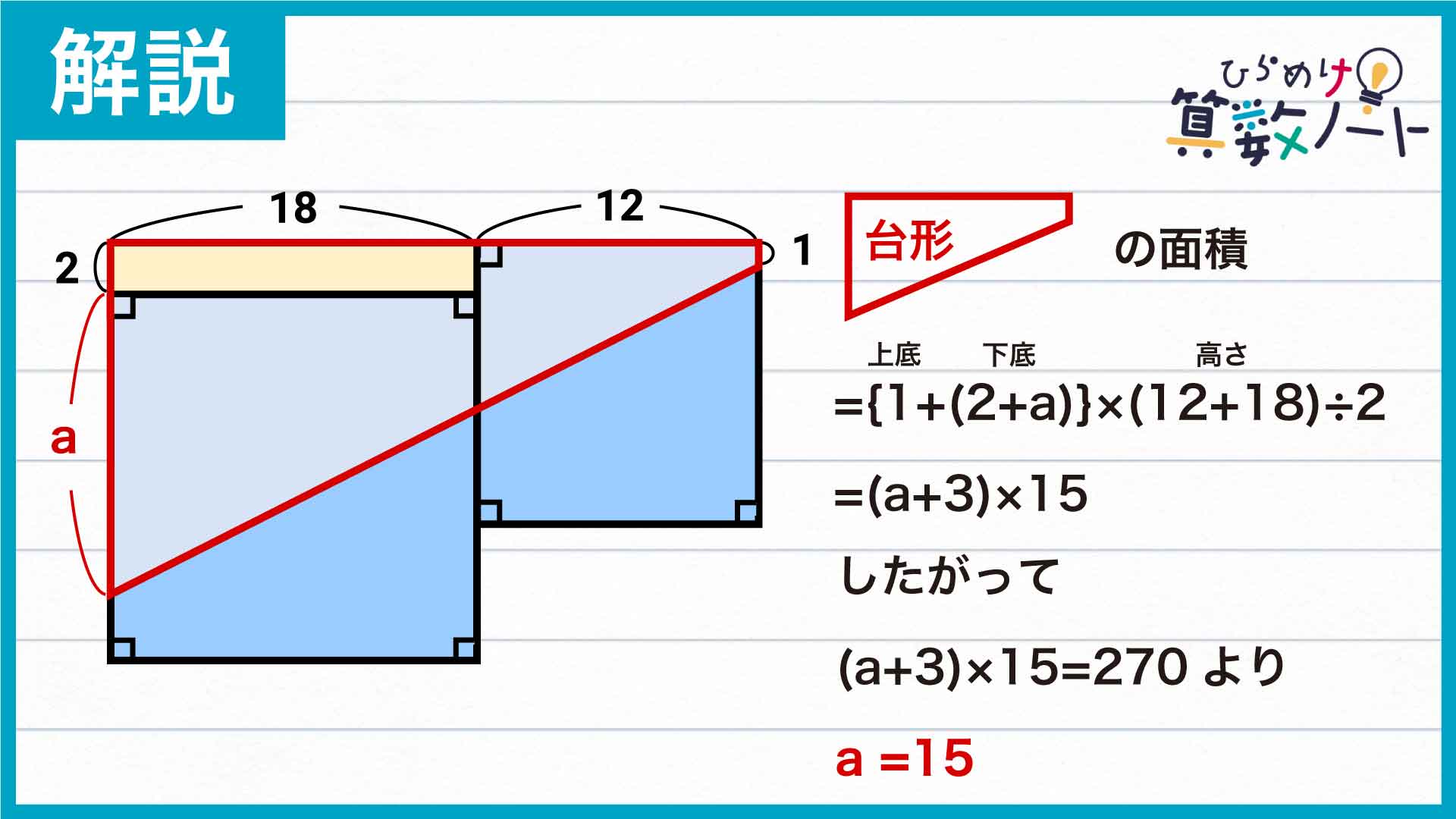
台形の面積は、{(上底)+(下底)}×(高さ)÷2で求められます。よって、この台形の面積は{1+(2+a)}×(12+18)÷2=(a+3)×15と表すこともできます。
したがって、台形の面積について(a+3)×15=270という式が成り立ちます。よって、求める長さはa=270÷15-3=15とわかるのです。
答え:15
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)







.jpg)







