解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
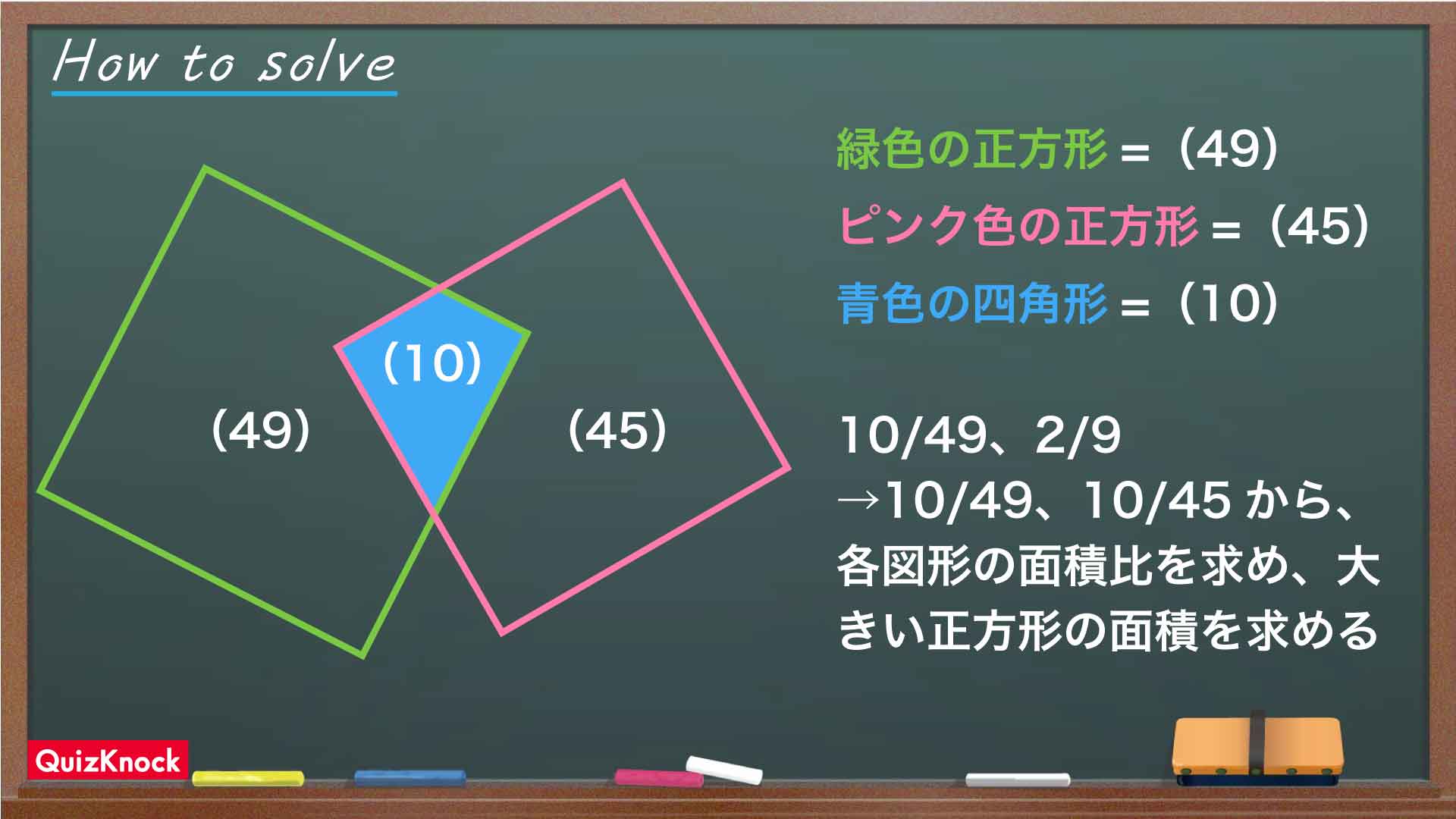
今回の解き方をまとめた図がこちらです。
今回のポイントは、「各図形の面積比を考えてから、大きい正方形の具体的な面積を求める」ことです。
このポイントをもとに、問題を攻略していきましょう!
各図形の面積比を考える
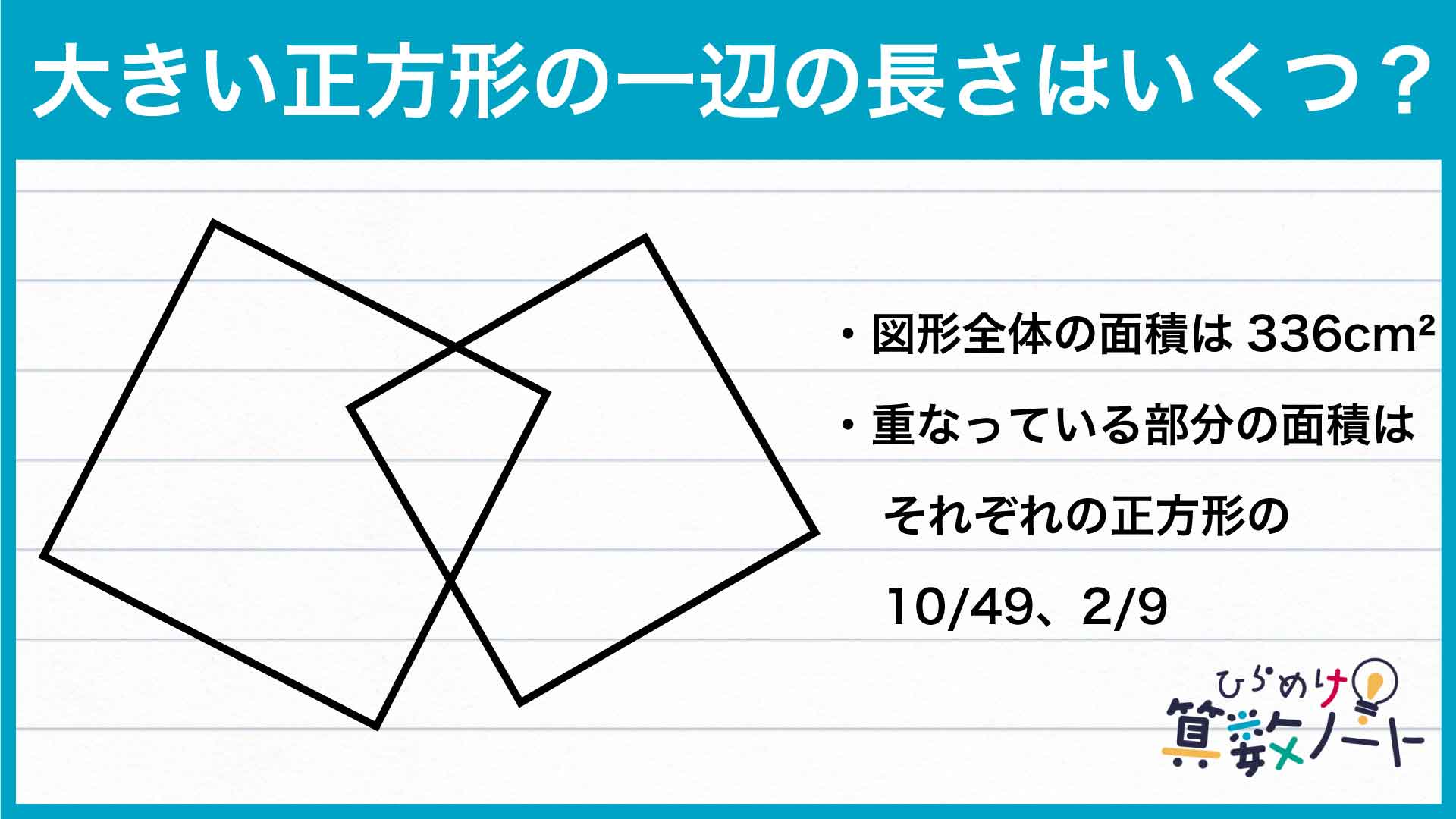
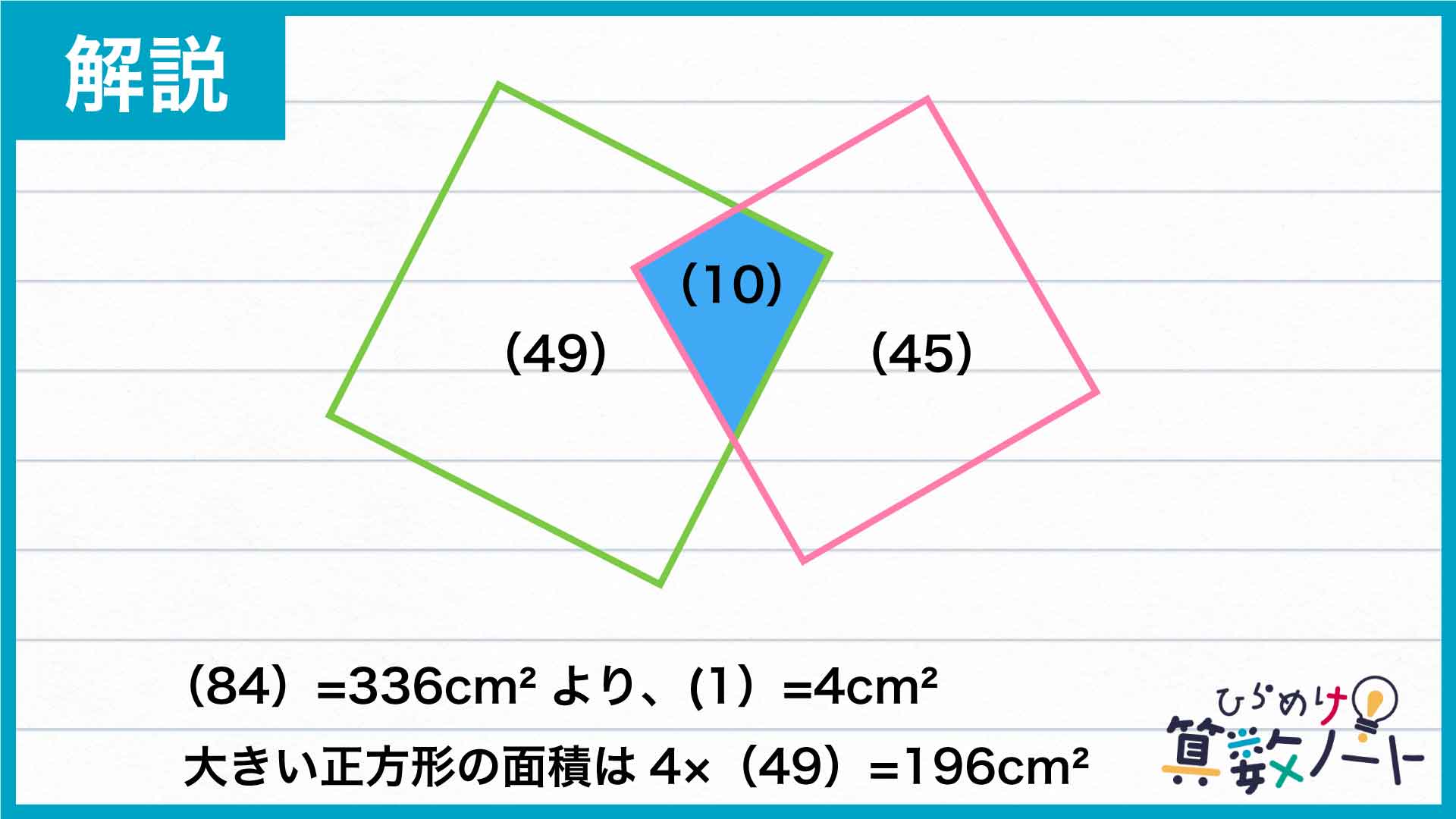
下の図で青色に塗った正方形が重なっている部分の面積は、それぞれの正方形の10/49、2/9です。分子の大きさを揃えると10/49、10/45となります。
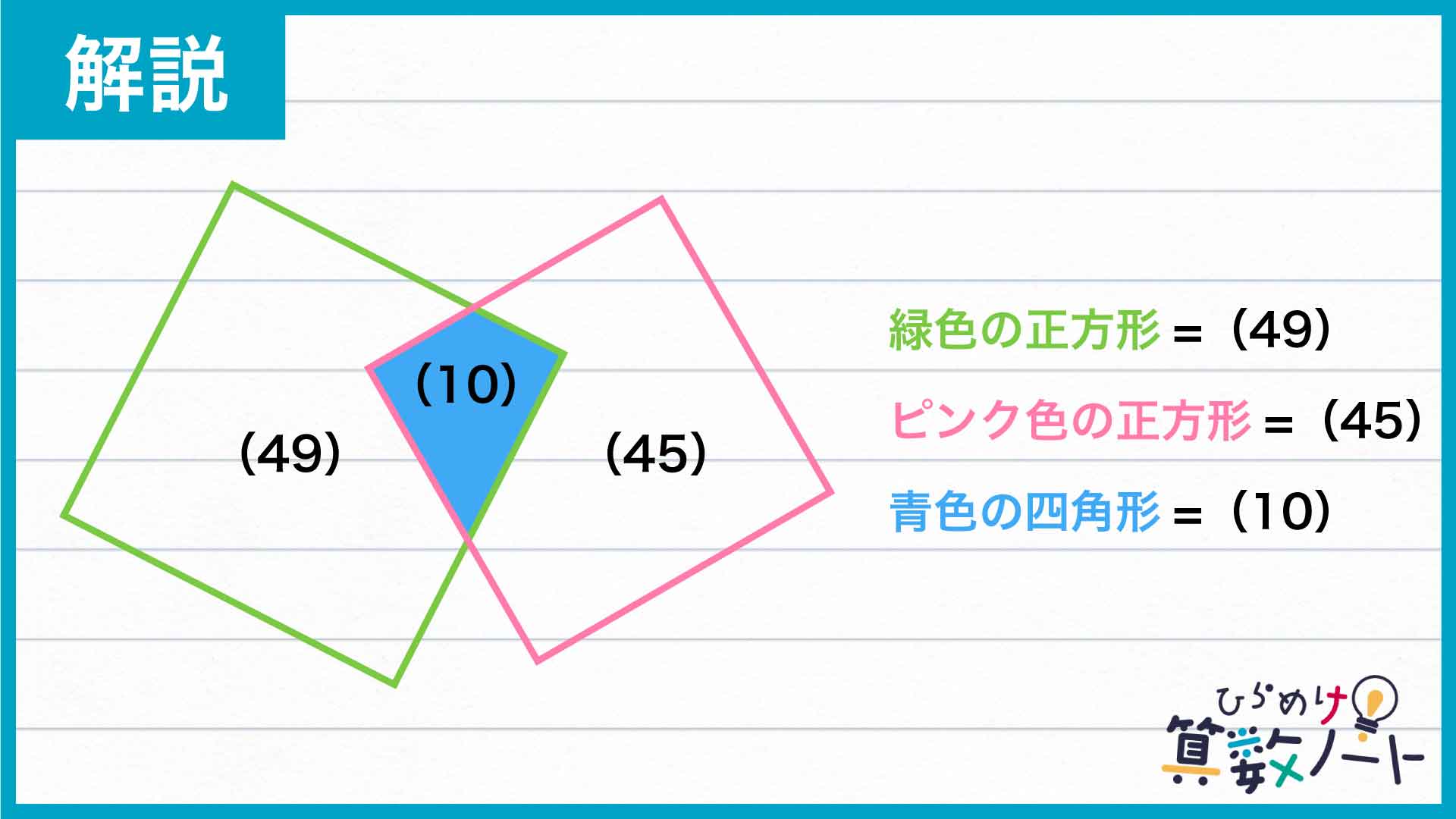
ここで、青色に塗った図形の面積を仮に(10)と表すとすると、大きい正方形の面積は(49)、小さい正方形の面積は(45)と表されます。
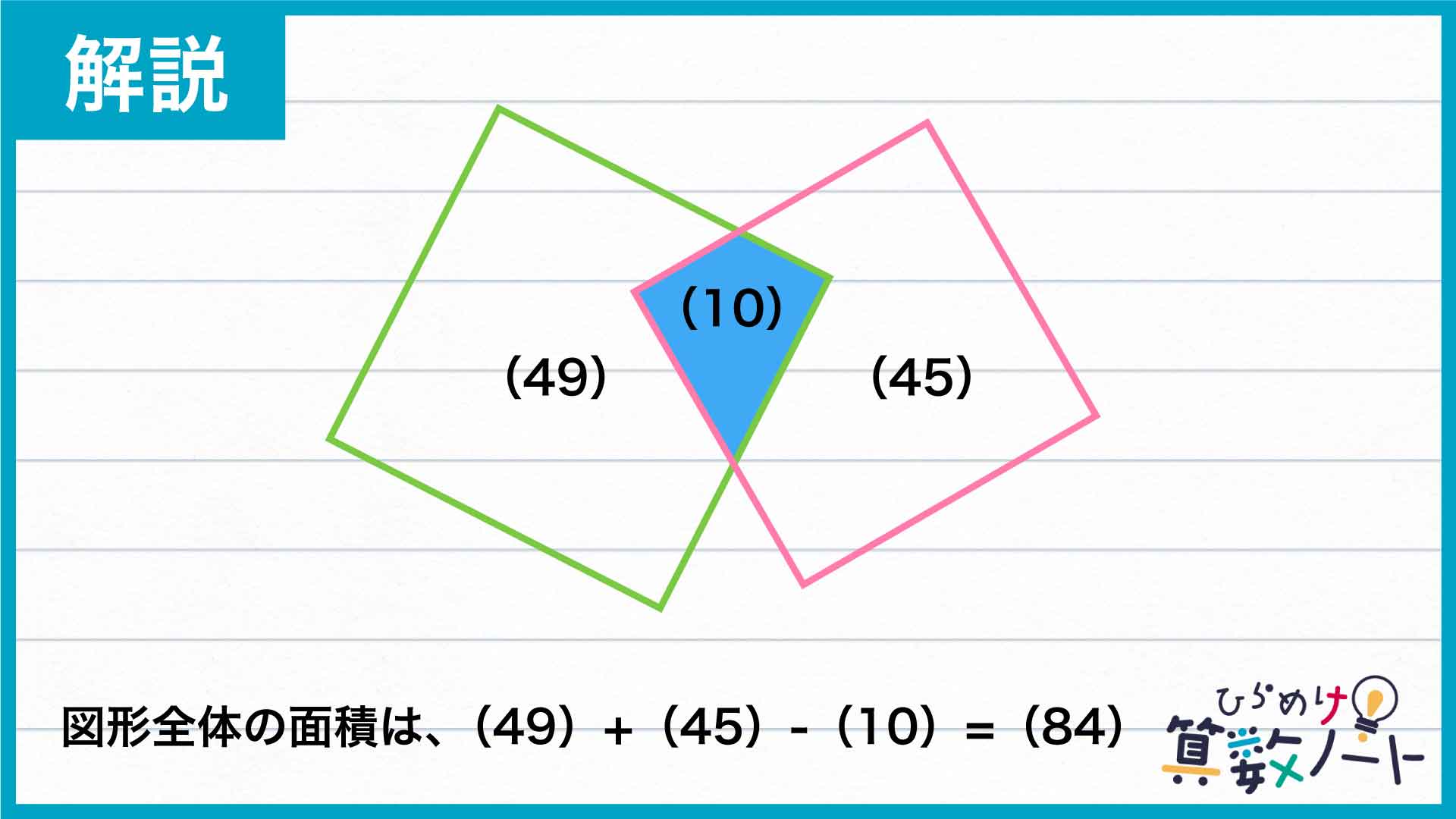
したがって、図形全体の面積は、(49)+(45)-(10)=(84)と表すことができます。
比を面積の数字に落とし込む
図形全体の面積は336cm2なので、(84)=336cm2より、(1)=4cm2と求めることができます。
したがって、大きい正方形の面積は、4×(49)=196cm2となります。
以上より、14×14=196であることから、大きい正方形の一辺の長さは14cmとなります。
答え:14cm
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)










.jpg)







