解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回の解き方をまとめた図がこちらです。
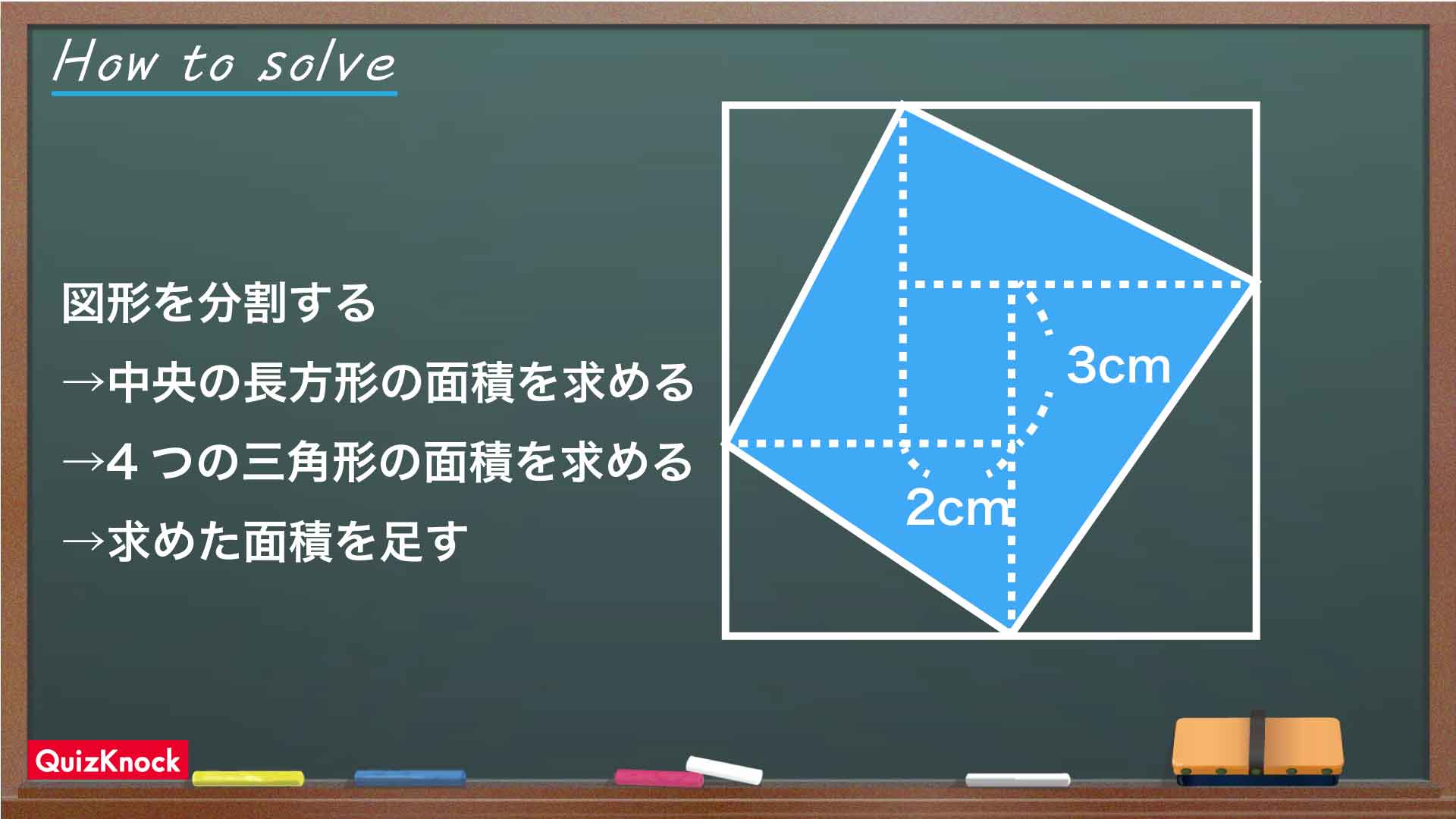
今回のポイントは、「補助線を引いて、図形を分割する」ことです。
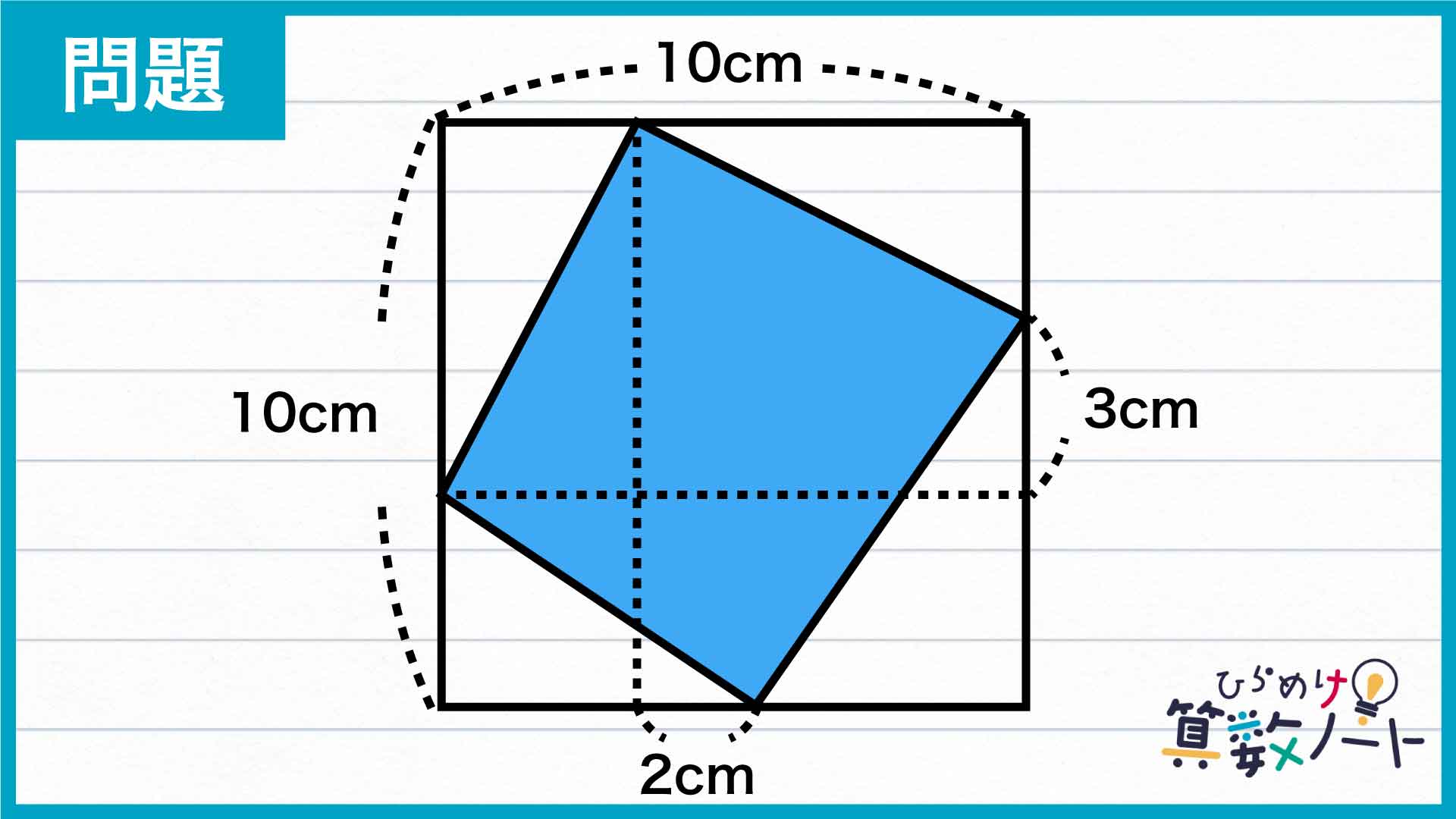
このポイントをもとに、問題を攻略していきましょう!
補助線を引く
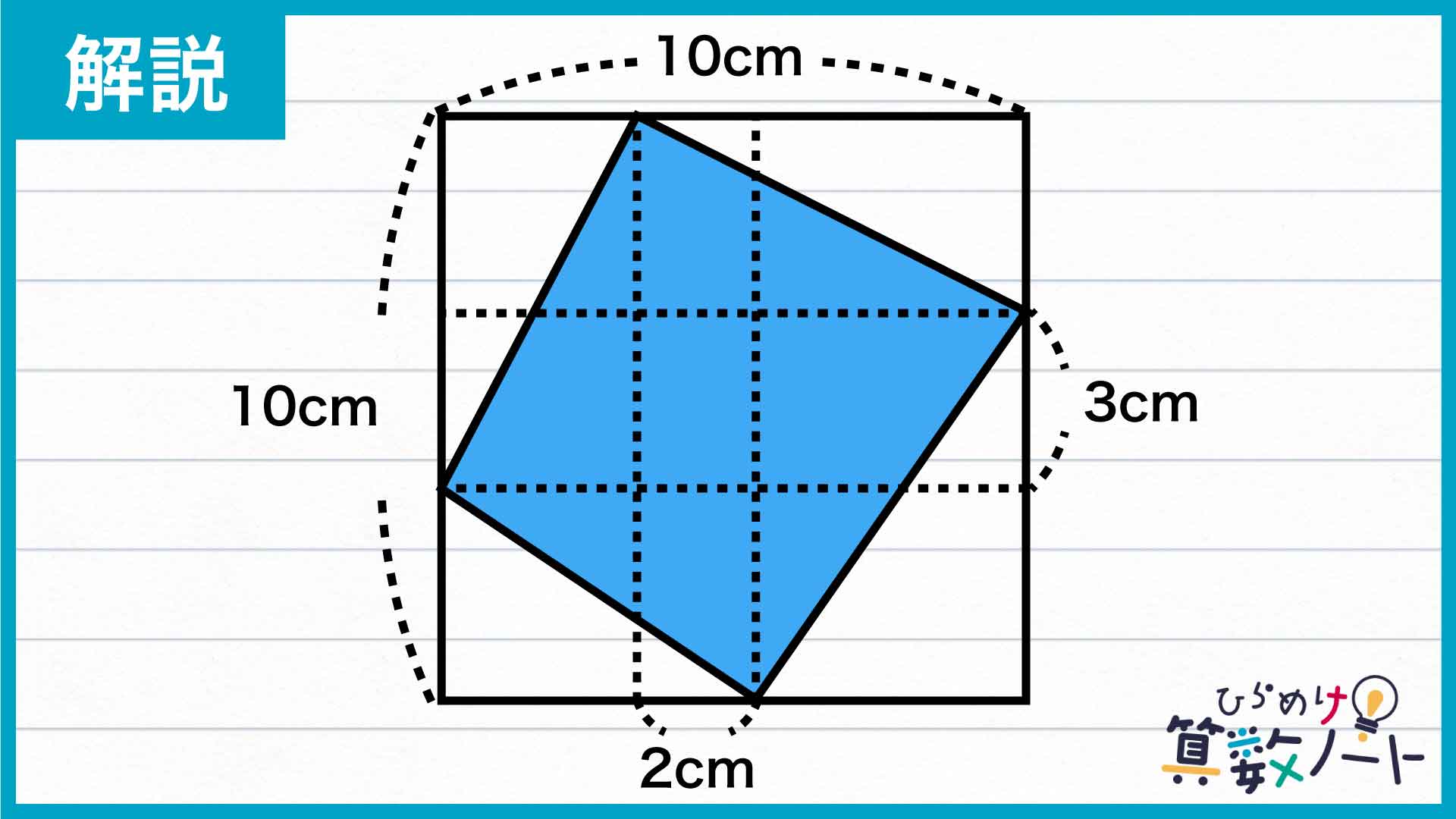
まず、最初に引かれていた2本の線と平行な線をそれぞれ、青色の四角形の角を通るように引きます。
この4本の線の一部を下の図のように消すと、青色に塗られた図形の中に1つの長方形と4つの三角形が現れます。
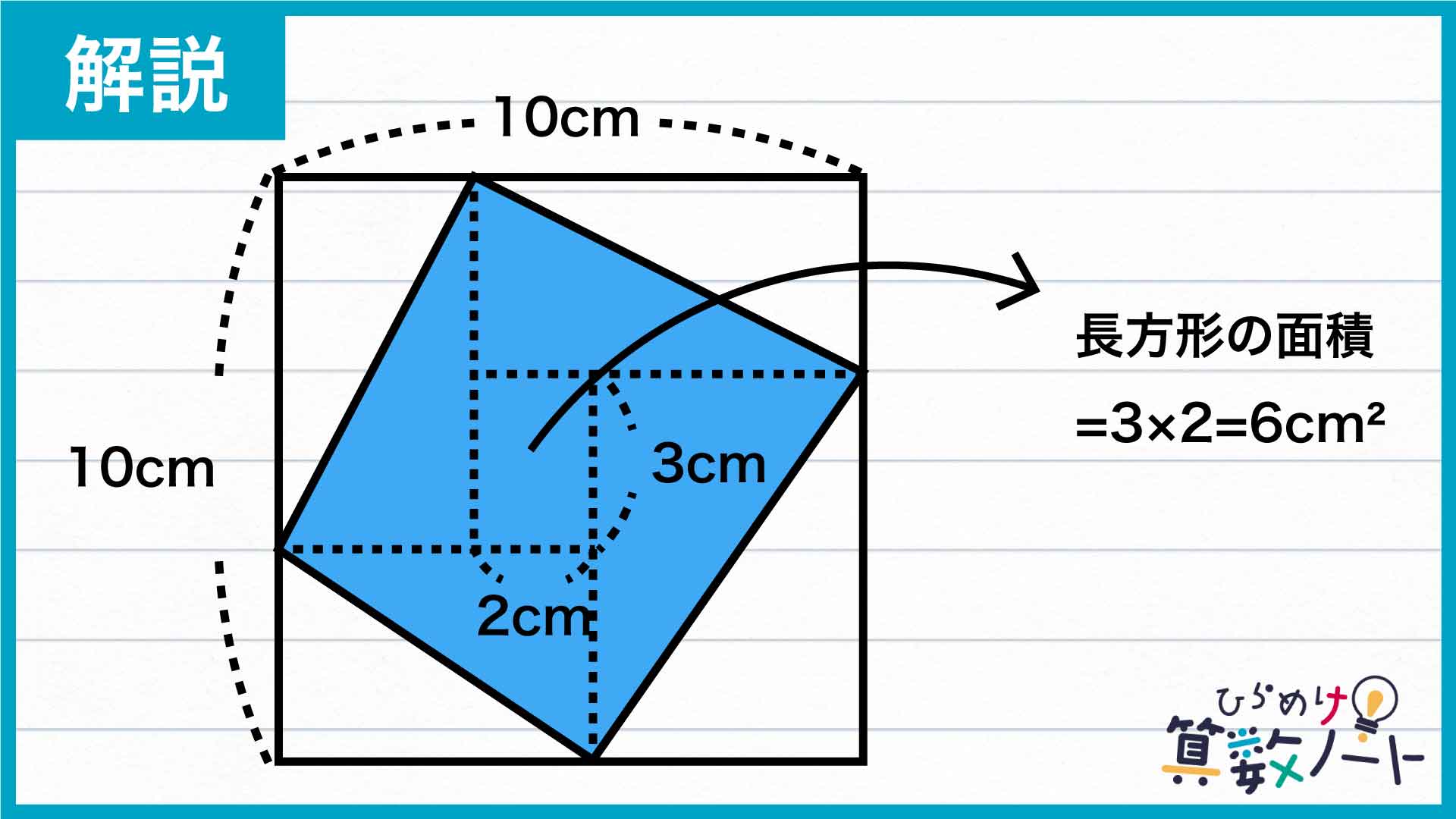
1つの長方形の面積を求める
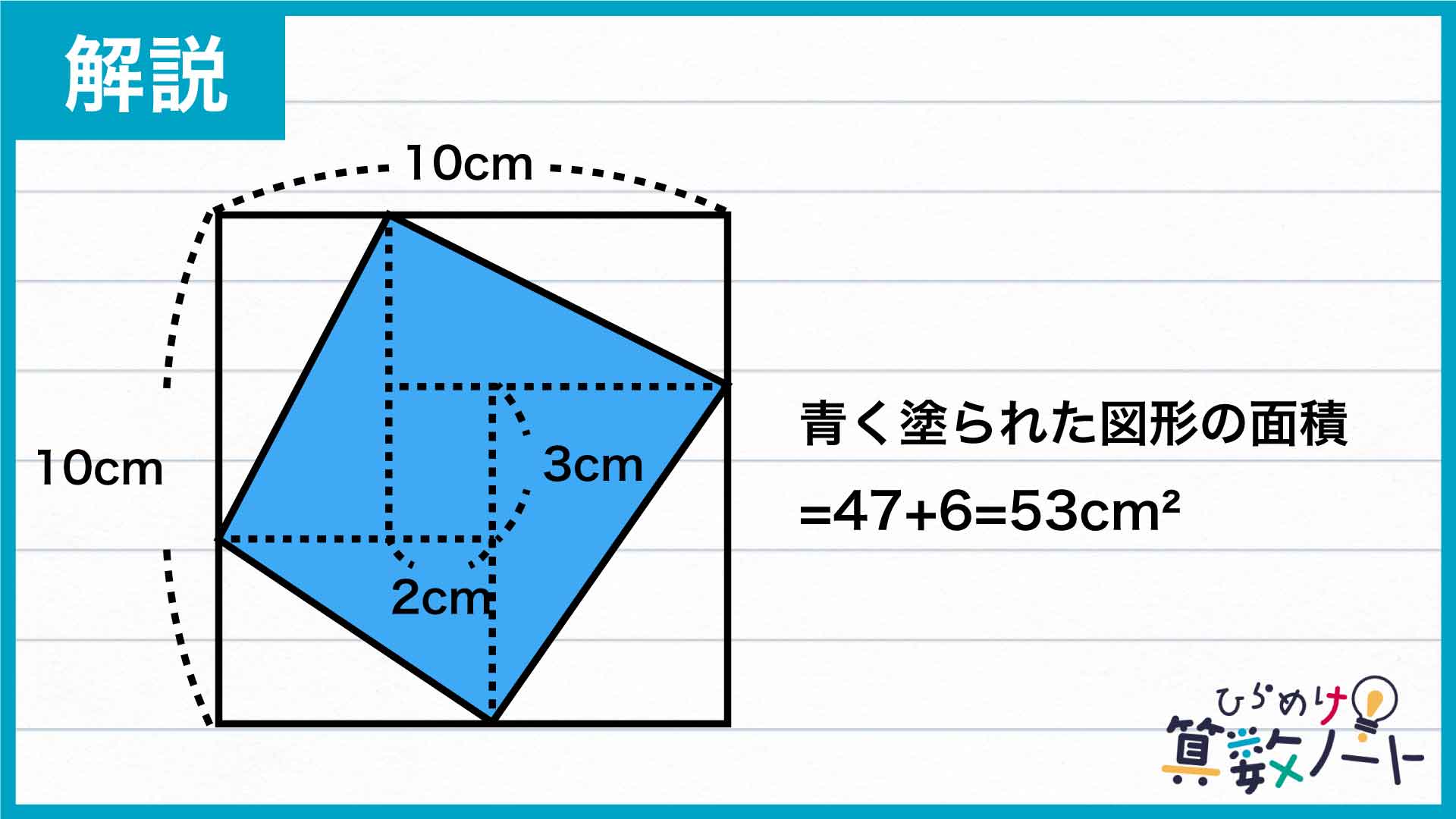
分割してできた図形のうち、中央にある長方形の面積は、最初の条件より3×2=6cm2と求めることができます。
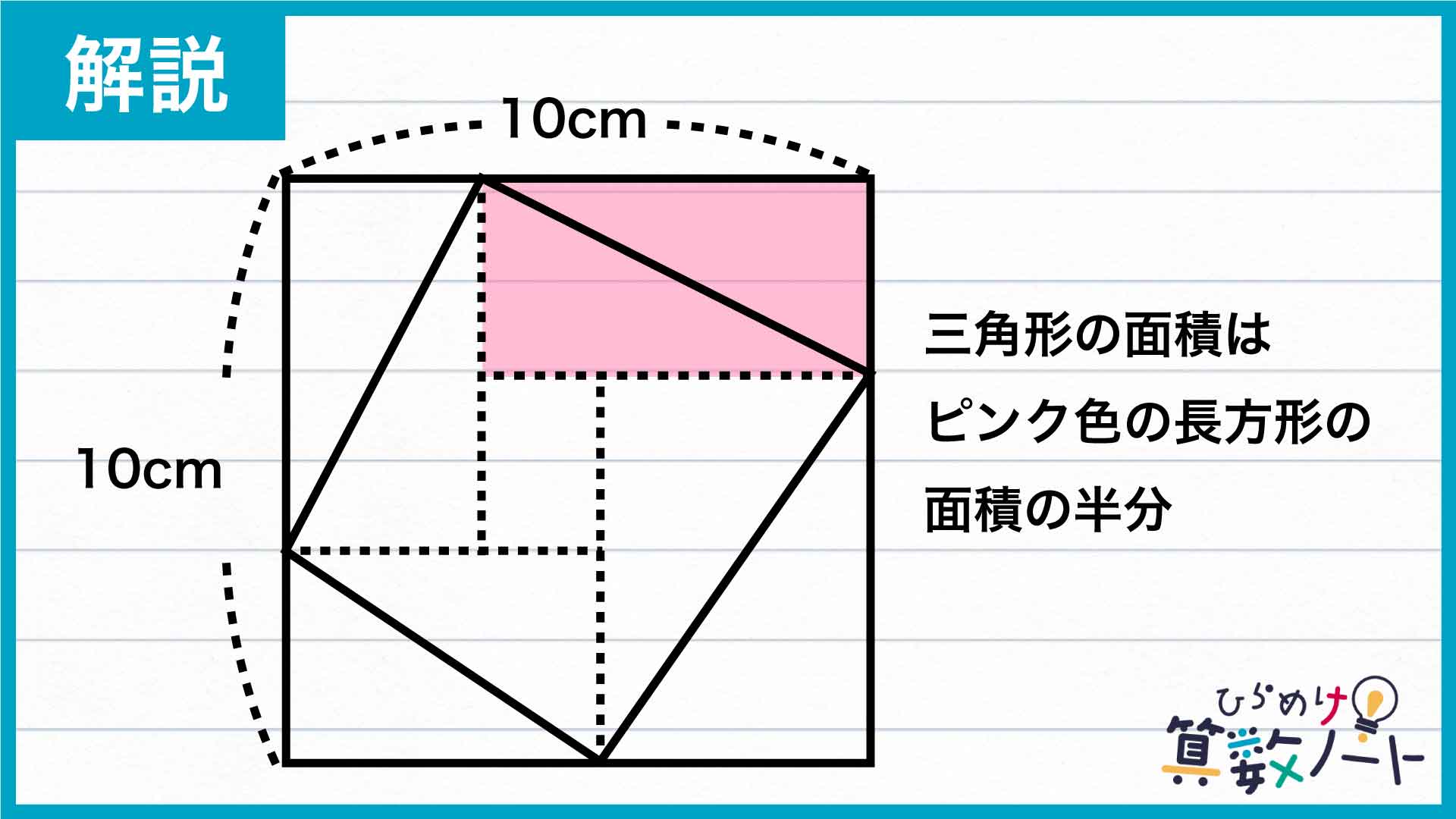
4つの三角形の面積を求める
続いて、4つの三角形の面積を求めます。
まず、右上の三角形に注目します。この三角形の面積は、下の図でピンク色に塗られた長方形の半分の面積であることがわかります。
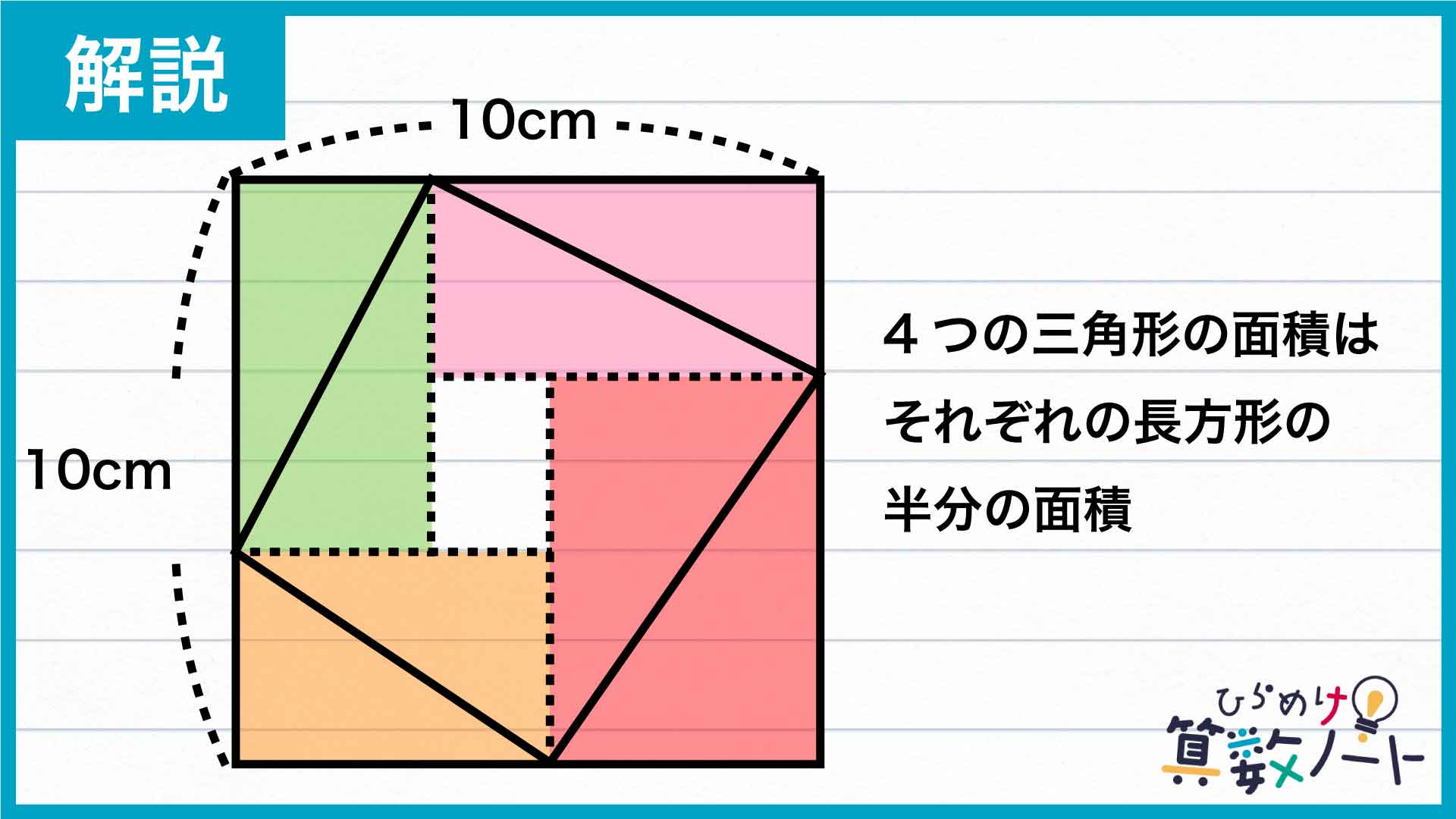
同様に、他の3つの三角形の面積はそれぞれ、下の図の緑色、オレンジ色、赤色の長方形の半分の面積です。
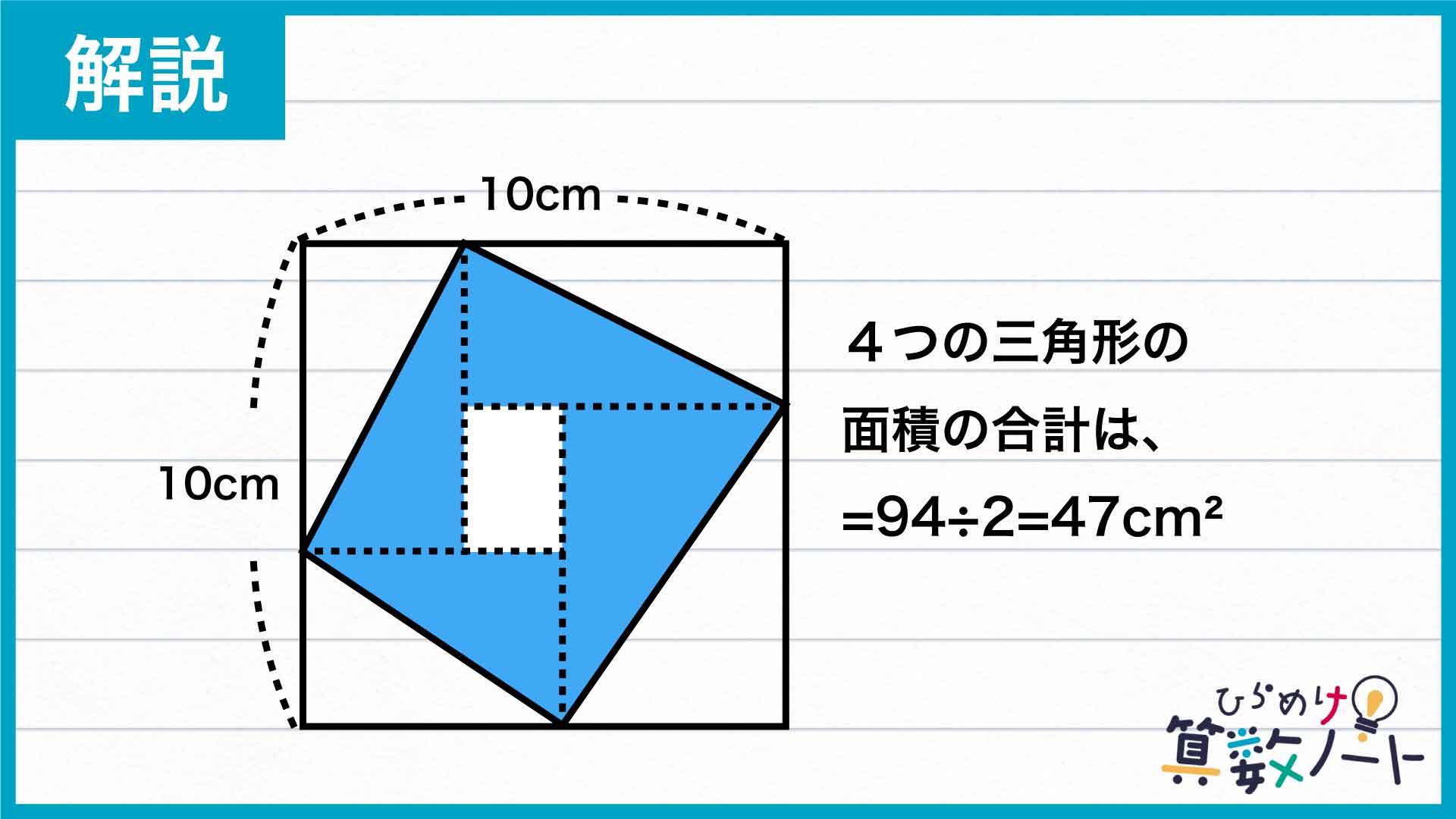
つまり、4つの三角形の面積の合計は、4色に塗られた長方形の面積の合計を半分にすることで求めることができます。
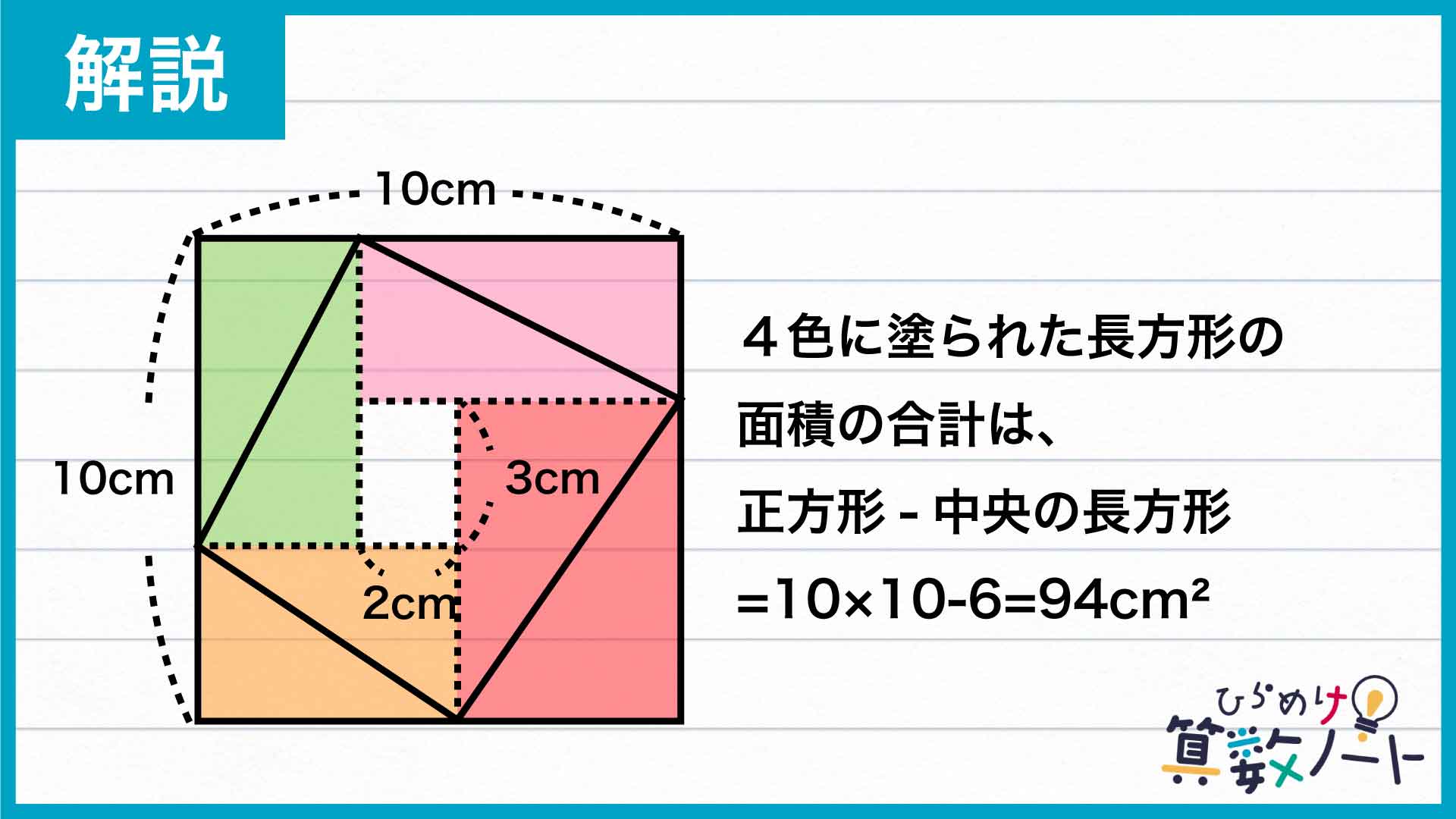
ここで、4色に塗られた長方形の面積の合計は、正方形から中央の長方形を引くことで求めることができ、10×10-6=94cm2です。
したがって、4つの三角形の面積の合計は、94÷2=47cm2となります。
青色に塗った図形の面積を求める
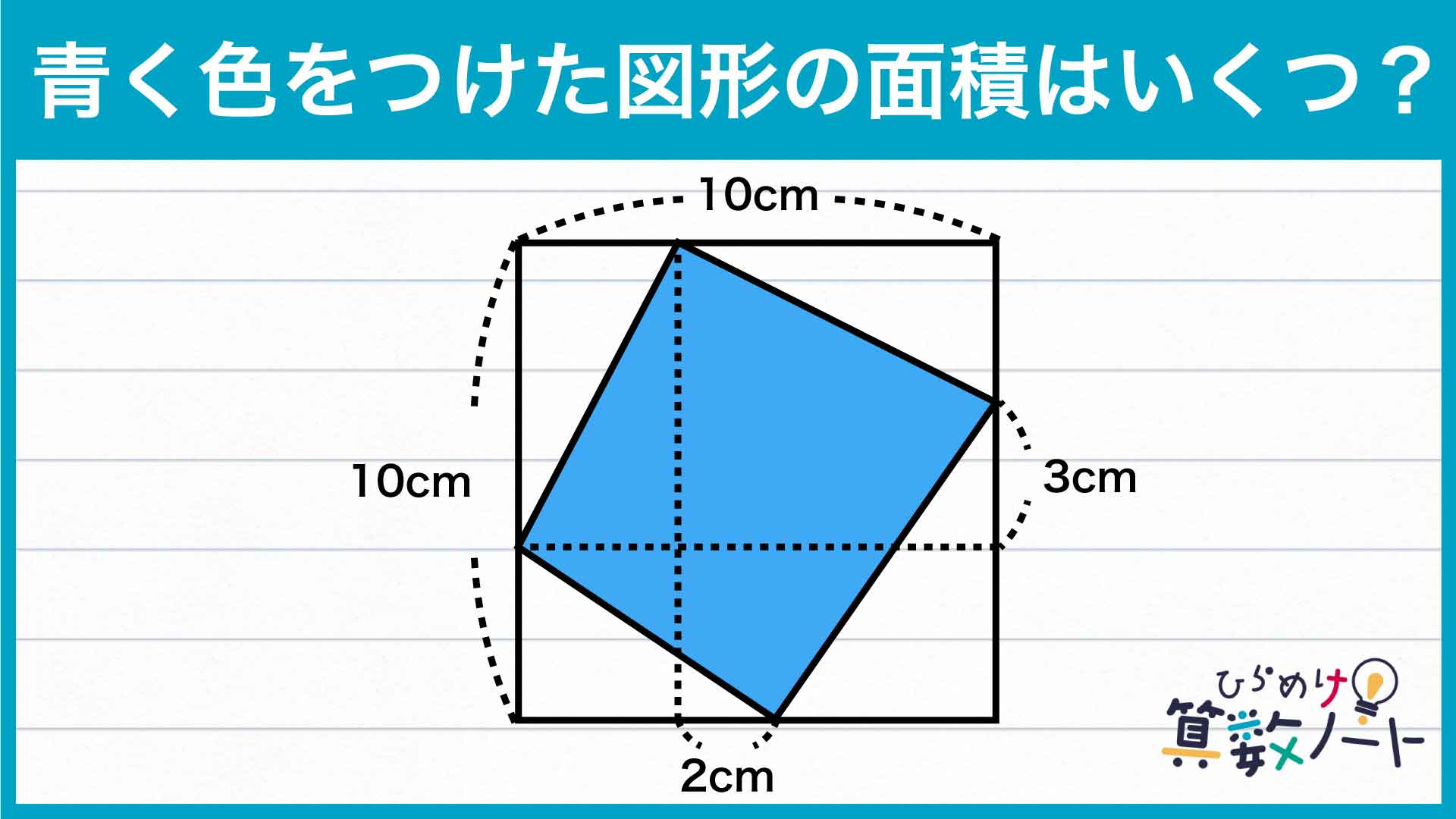
以上より、青色に塗った図形の面積は、6+47=53cm2となります。
答え:53cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)










.jpg)






