解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
整理すると、
- 合同な三角形の組(三角形ABCと三角形DBC)に注目する
- 三角形CDEが二等辺三角形であることを利用する
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
合同な三角形の組に注目する
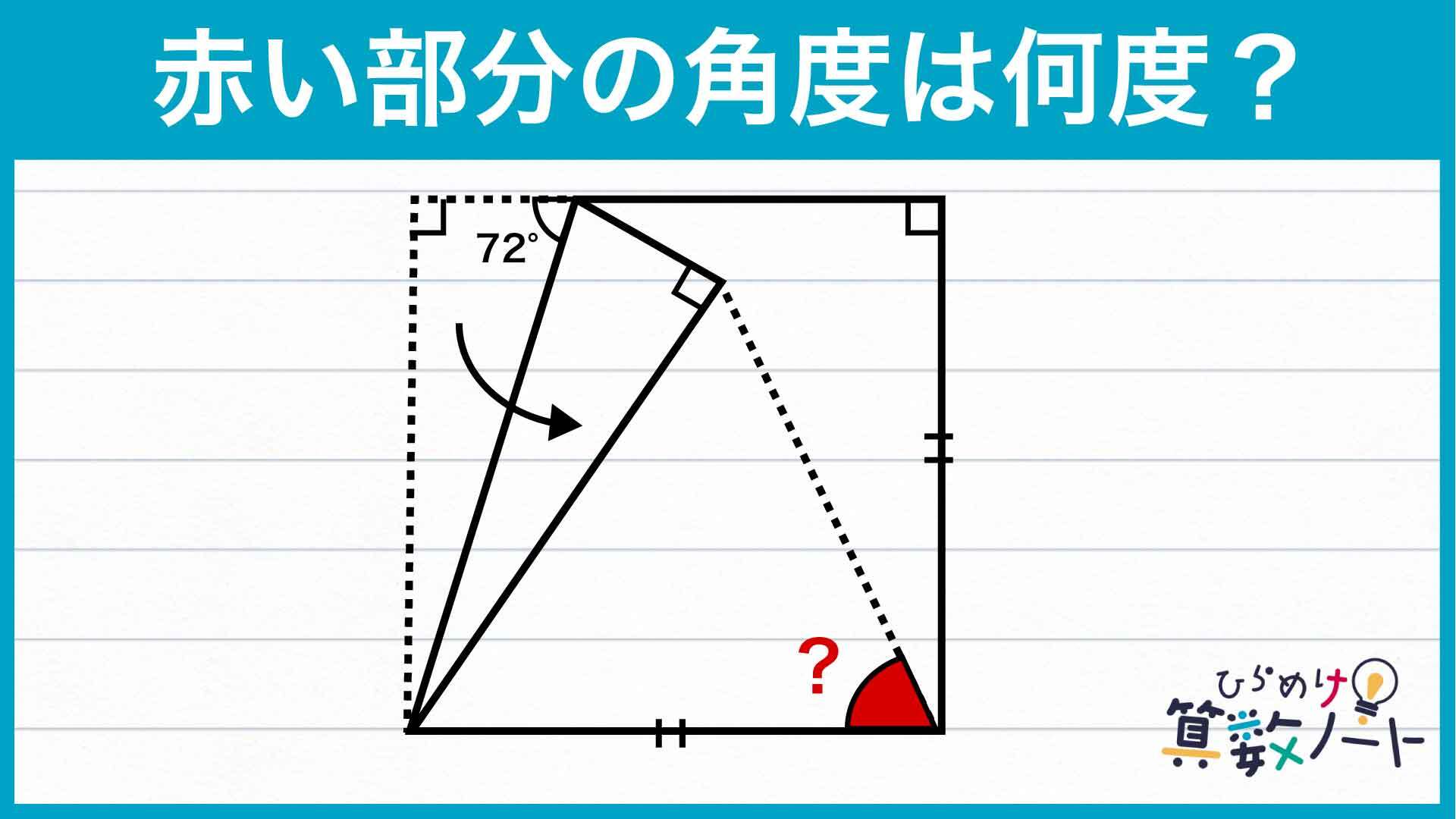
まず、三角形DBCは三角形ABCを折り返してできた三角形なので、三角形ABCと三角形DBCは合同な三角形になります。したがって、合同な三角形の対応する辺の長さと対応する角度の大きさは等しいことから、AC=DC、角ACB=角DCBであることがわかります。
角ABCの大きさは問題の条件から72度なので、角ACBの大きさは180-(90+72)=18度となります。よって、角ACB=角DCBであることから、角DCB=18度となり、角DCEの大きさは90-(18+18)=54度になります。
三角形CDEが二等辺三角形であることを利用する
四角形ACEFが正方形であるという条件から、ACとCEの長さは等しいです。したがって、DC=AC=CEより、三角形CDEはCD=CEの二等辺三角形であることがわかります。
二等辺三角形の2つの底角の大きさは等しいので、角CDE=角CEDです。角DCE=54度なので、角CDE=角CED=(180-54)÷2=63度になります。したがって、「?」に当たる角度は63度になることがわかります。
答え:63度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】














.jpg)









.jpg)






