解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
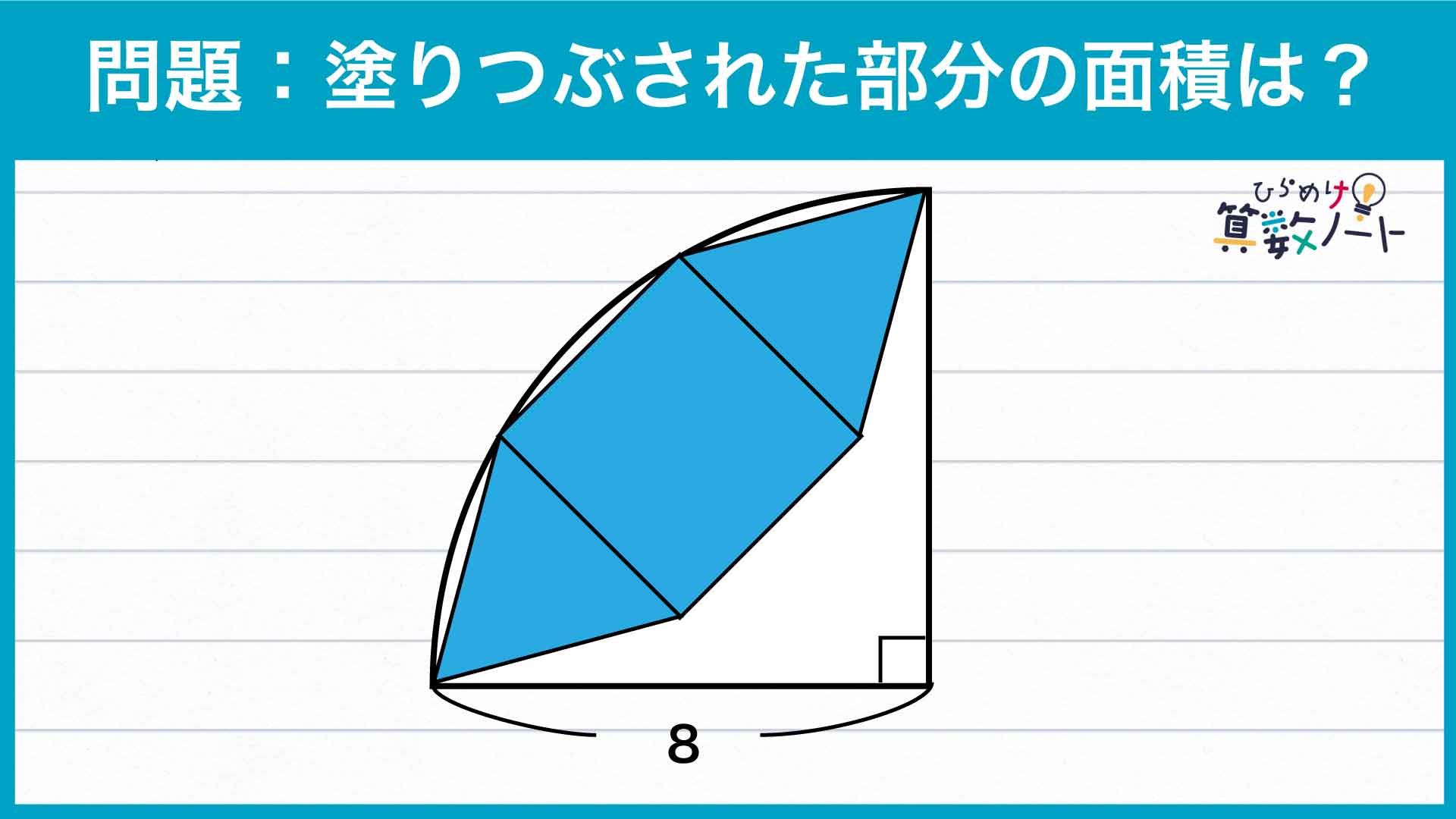
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
この問題の解き方をまとめた図がこちらです。
ポイントは、図形をなるべく単純な形に切り分けてからそれぞれの面積を求めて足し引きすることです。
では、このポイントを踏まえつつ解いていきましょう!
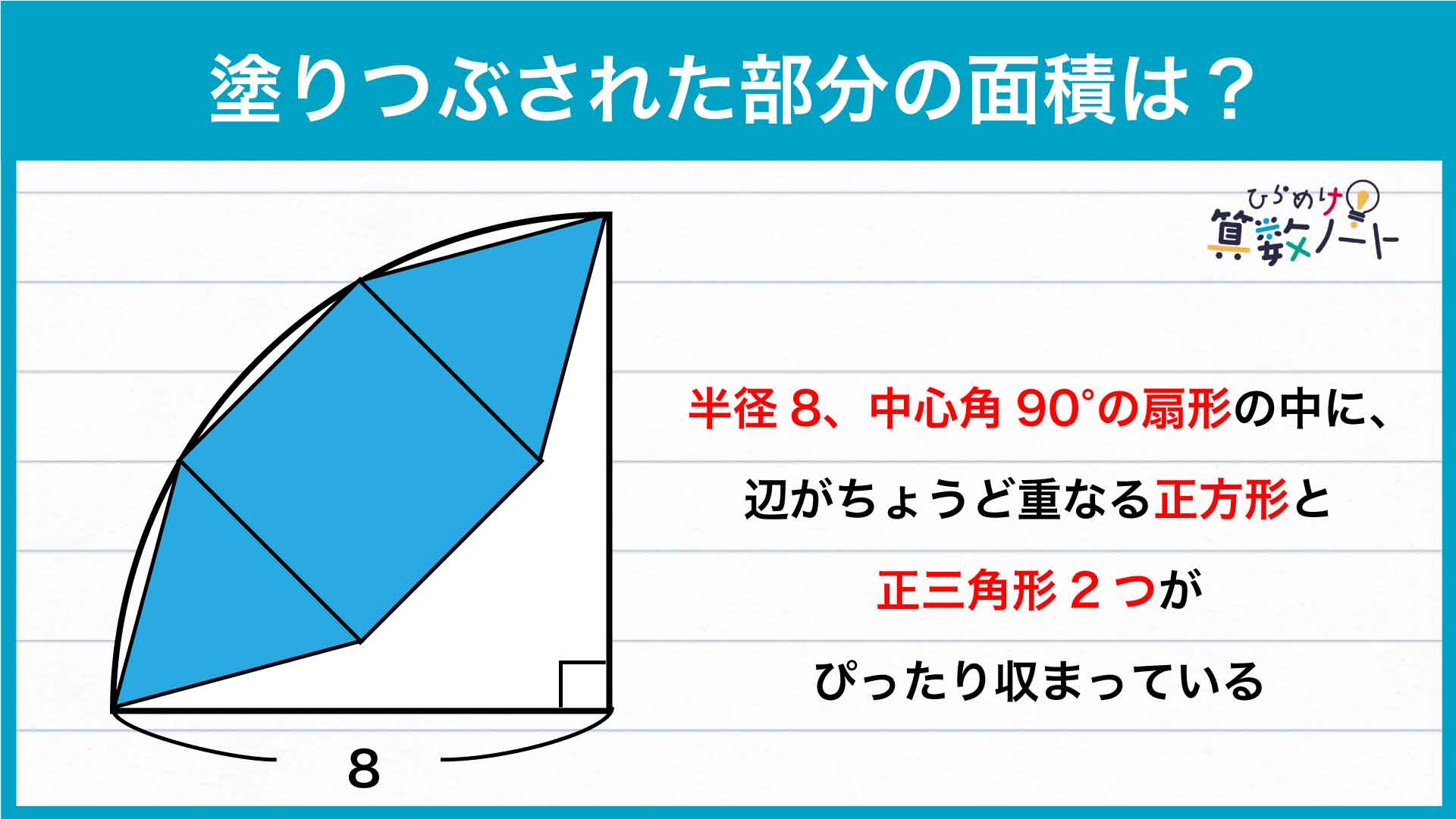
求める面積の半分に注目する
この問題は、正方形や正三角形の面積をバラバラに求めるのではなく、塗りつぶされた範囲を半分に割った部分の面積に注目することがカギとなります。
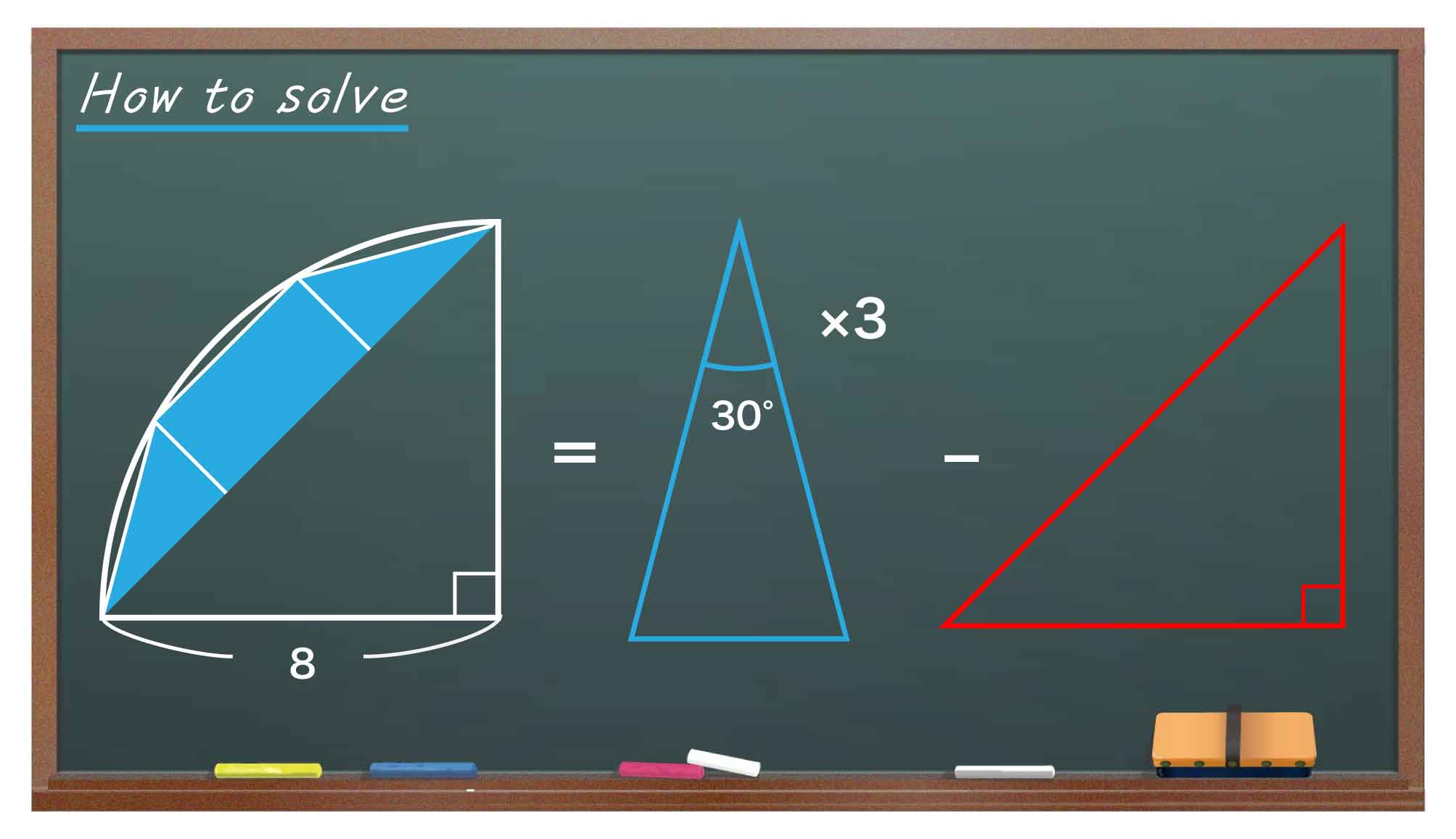
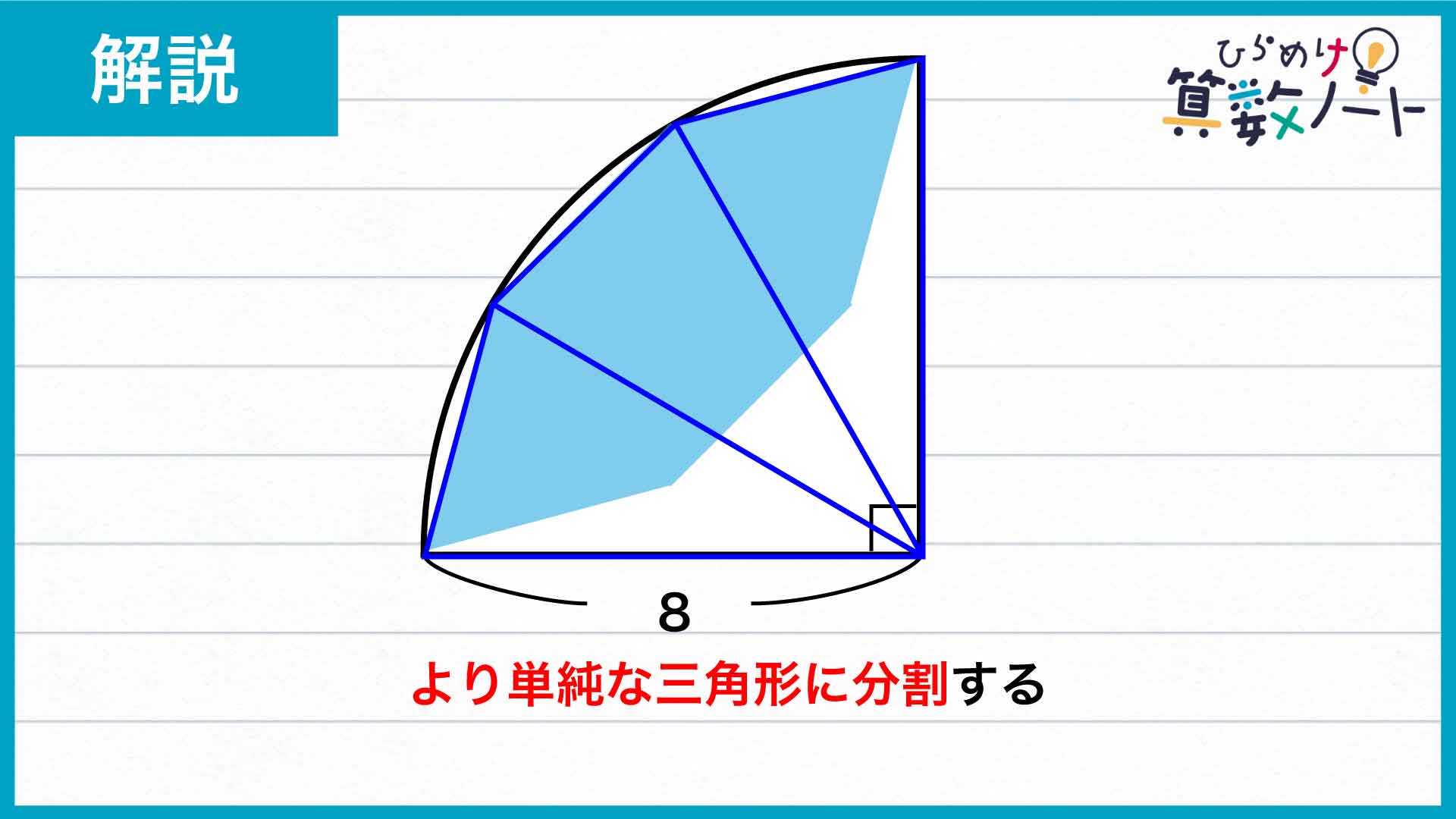
上の図の青線で囲まれた部分から赤線で囲まれた部分を引くことで、求める面積の半分を計算することができます。赤線で囲まれた部分は直角三角形ですが、青線で囲まれた部分はまだ少し複雑な形をしていますね。そこで、複雑な部分の面積を求めるために、より単純な三角形に分割してみます。
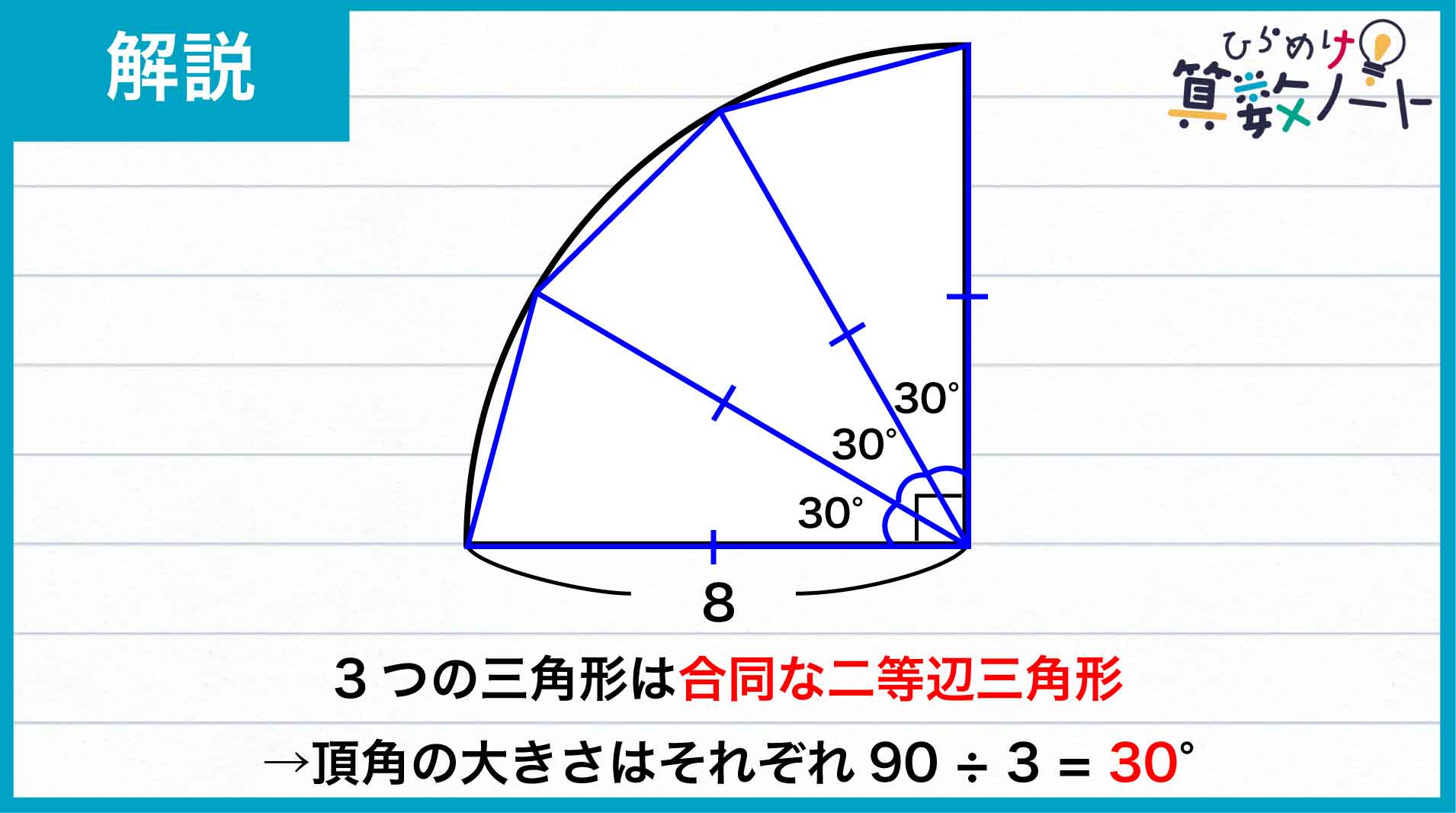
現れた3つの三角形は、3辺のうち2辺が同じ扇形の半径にあたります。さらに残った1辺も、同じ長さの辺を持つ正方形と正三角形の1辺に該当します。したがって3つの三角形は各辺の長さが等しいことから、合同な二等辺三角形であるとわかるのです。
この二等辺三角形の頂角(長さの等しい2辺にはさまれた角)が3つ集まると90度なので、頂角の大きさはそれぞれ90÷3=30度です。
三角形の面積をそれぞれ求める
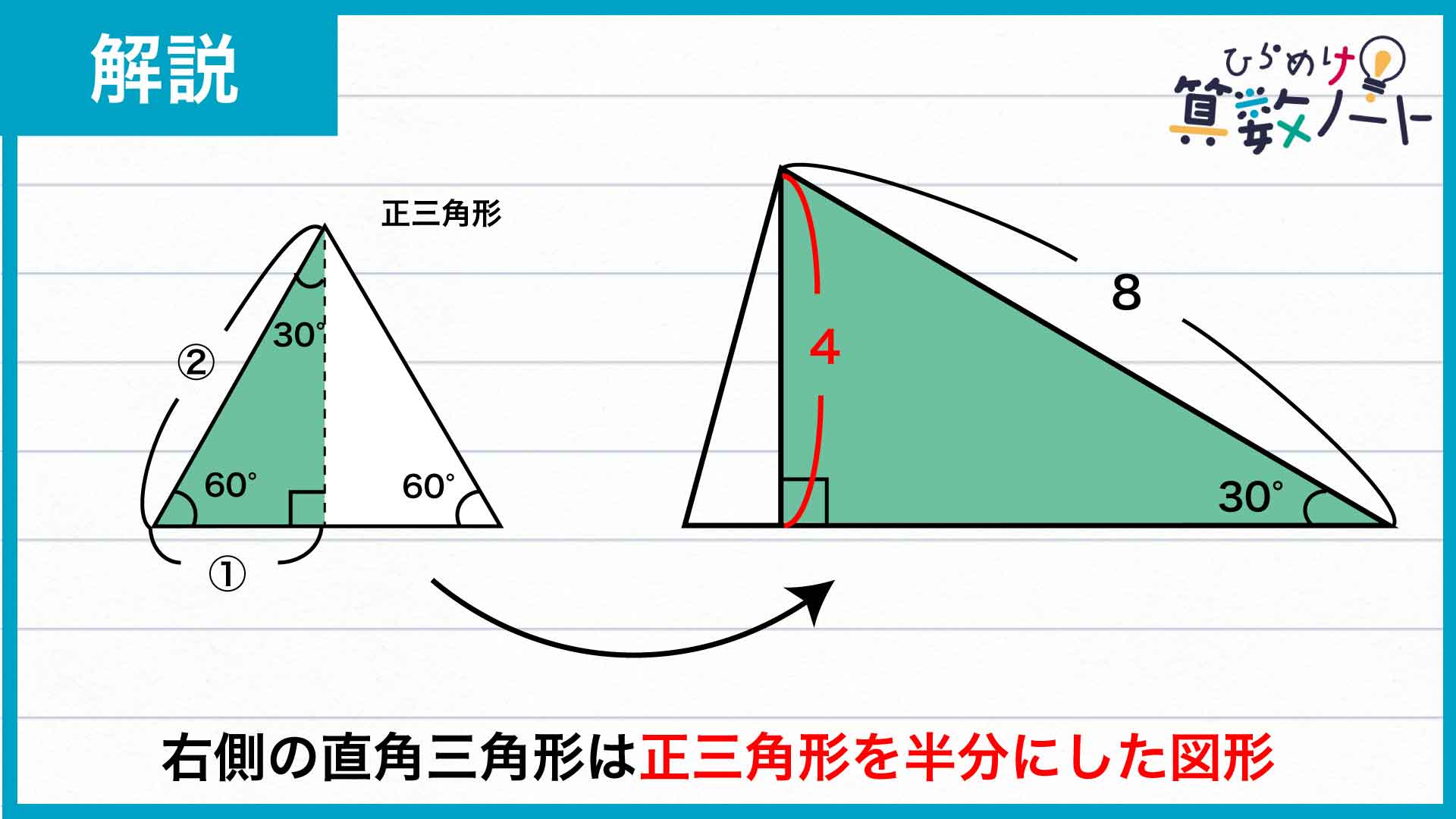
頂角30度の二等辺三角形について、下の図のように1辺に対して垂直な線を引きます。
このとき、右側の直角三角形は30度の角を持つことから、三角定規でもお馴染みの正三角形を半分にした図形であるといえます。したがって、長さ8の辺を底辺としたときの高さは8÷2=4であることがわかります。
よって、頂角30度の二等辺三角形1つの面積は8×4÷2=16です。
再び全体の面積に注目してみましょう。求める面積の半分は、頂角30度の二等辺三角形3つの面積から直角二等辺三角形1つの面積を引いたものと等しくなります。
直角三角形は底辺・高さともに8なので、その面積は8×8÷2=32。よって、求める面積の半分は16×3-32=16です。したがって、求める面積は16×2=32であるとわかるのです。
答え:32
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】













.jpg)










.jpg)







