解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
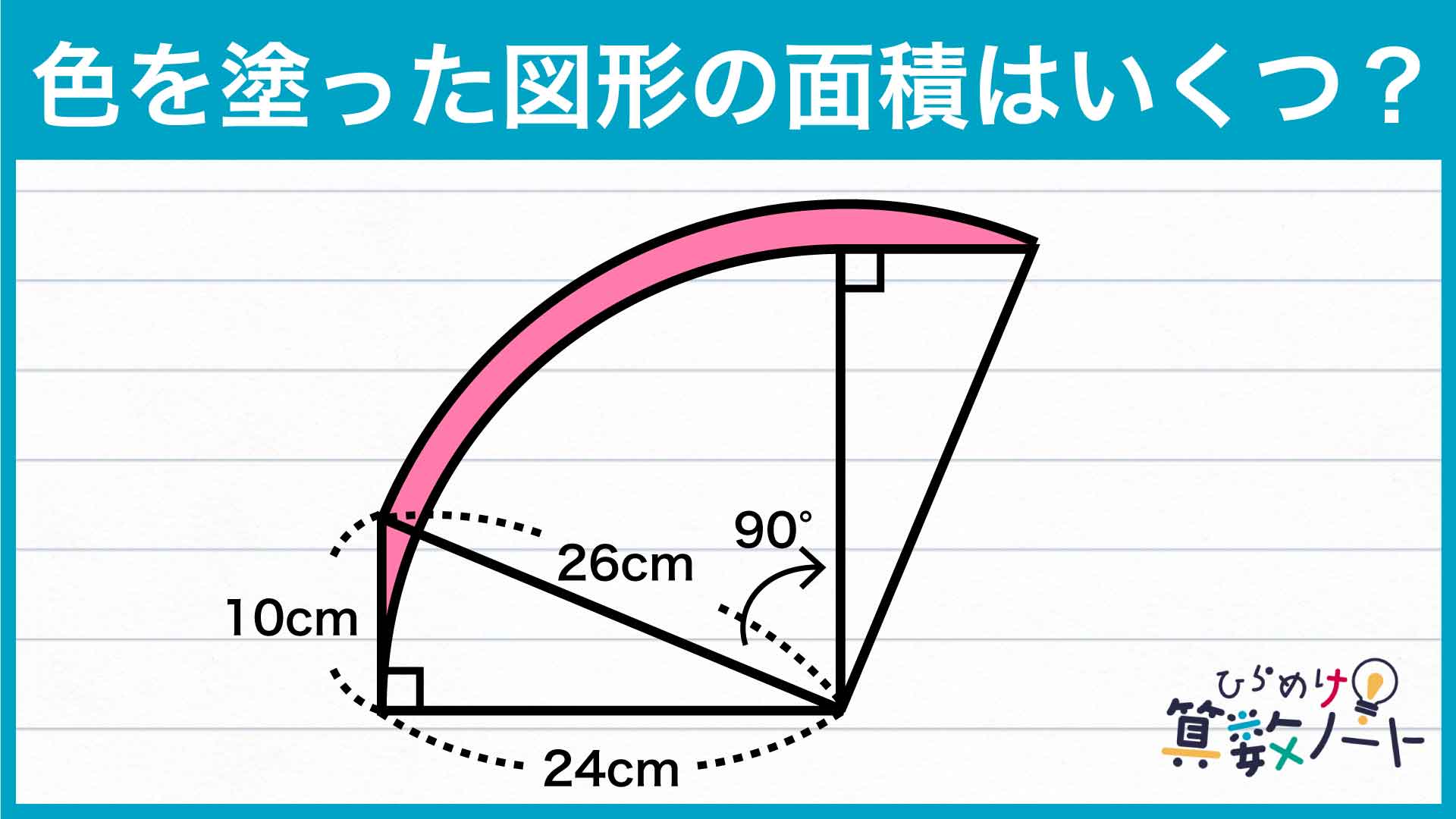
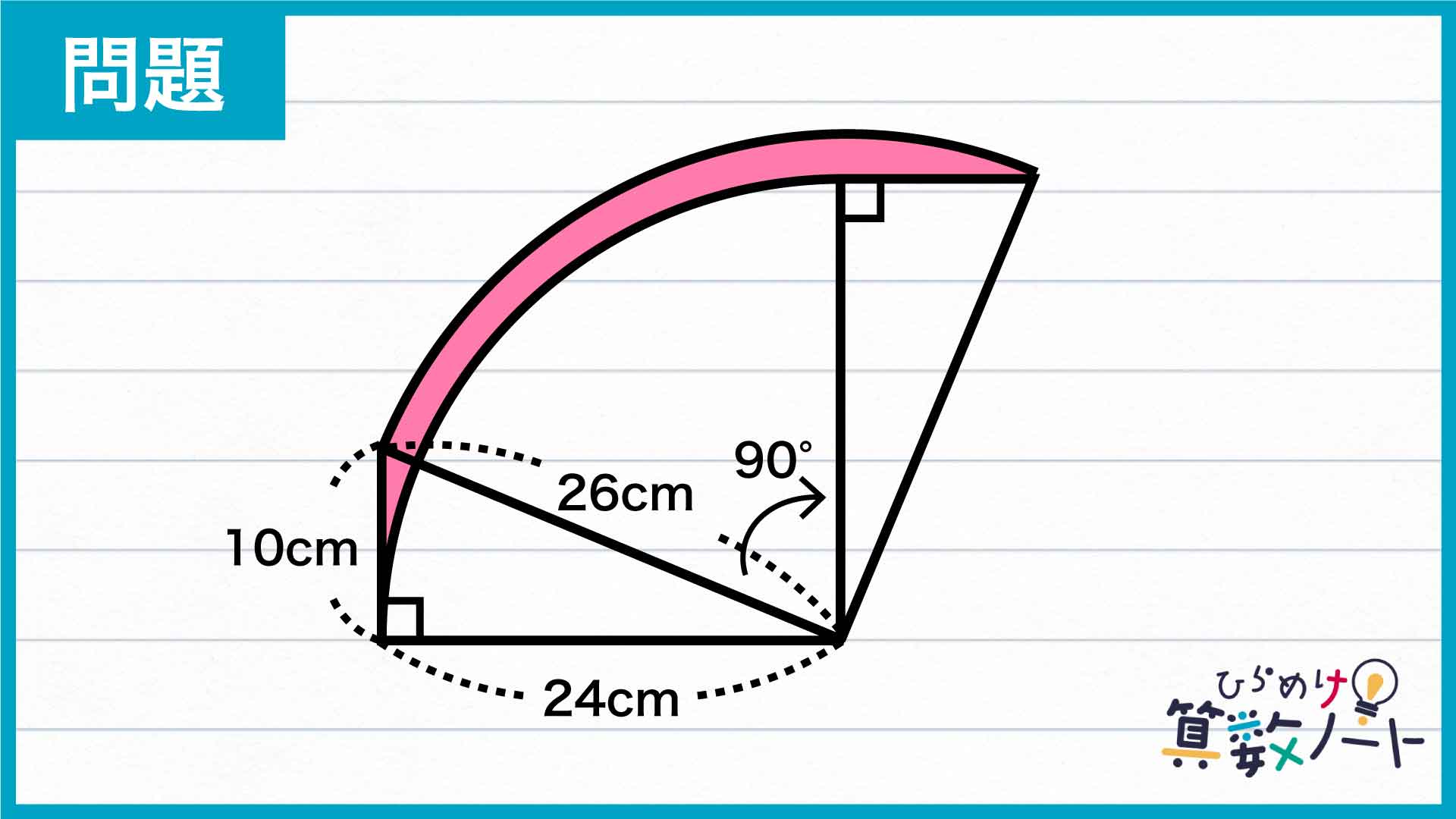
今回の解き方をまとめた図がこちらです。
今回のポイントは、「ピンク色で塗られた図形がどのようにできたのかを観察する」ことです。
このポイントをもとに、問題を攻略していきましょう!
三角形の回転によってできた図形を確認する
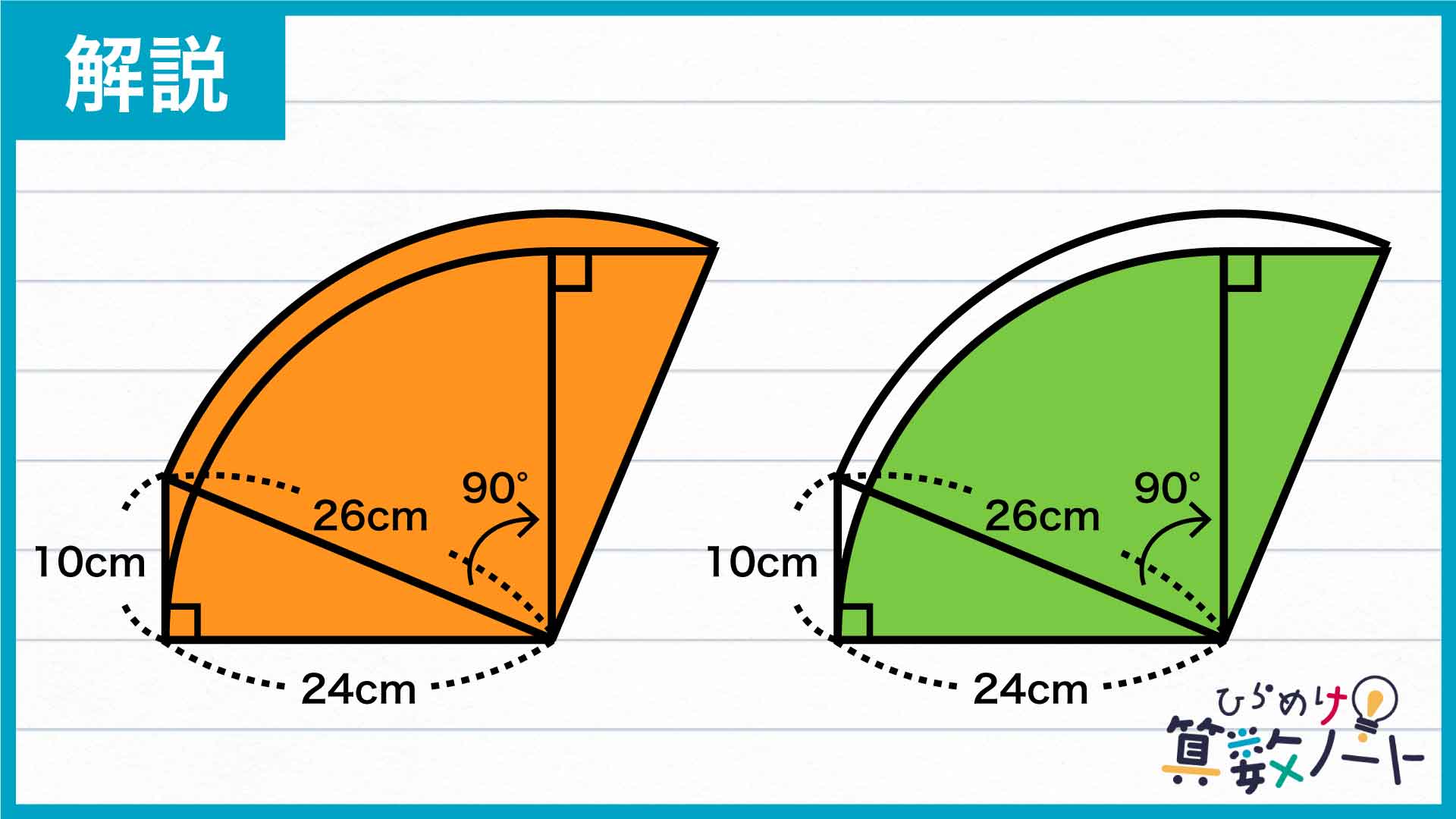
三角形を回転させたことにより、三角形の長さが26cmの辺を半径にした扇形と、24cmの辺を半径にした扇形ができていることがわかります。
中心角の大きさはどちらも90度です。円は1周360度なので、この扇形は円を4等分したものとなります。
「ピンク色の図形」と「三角形と扇形」の関係を調べる
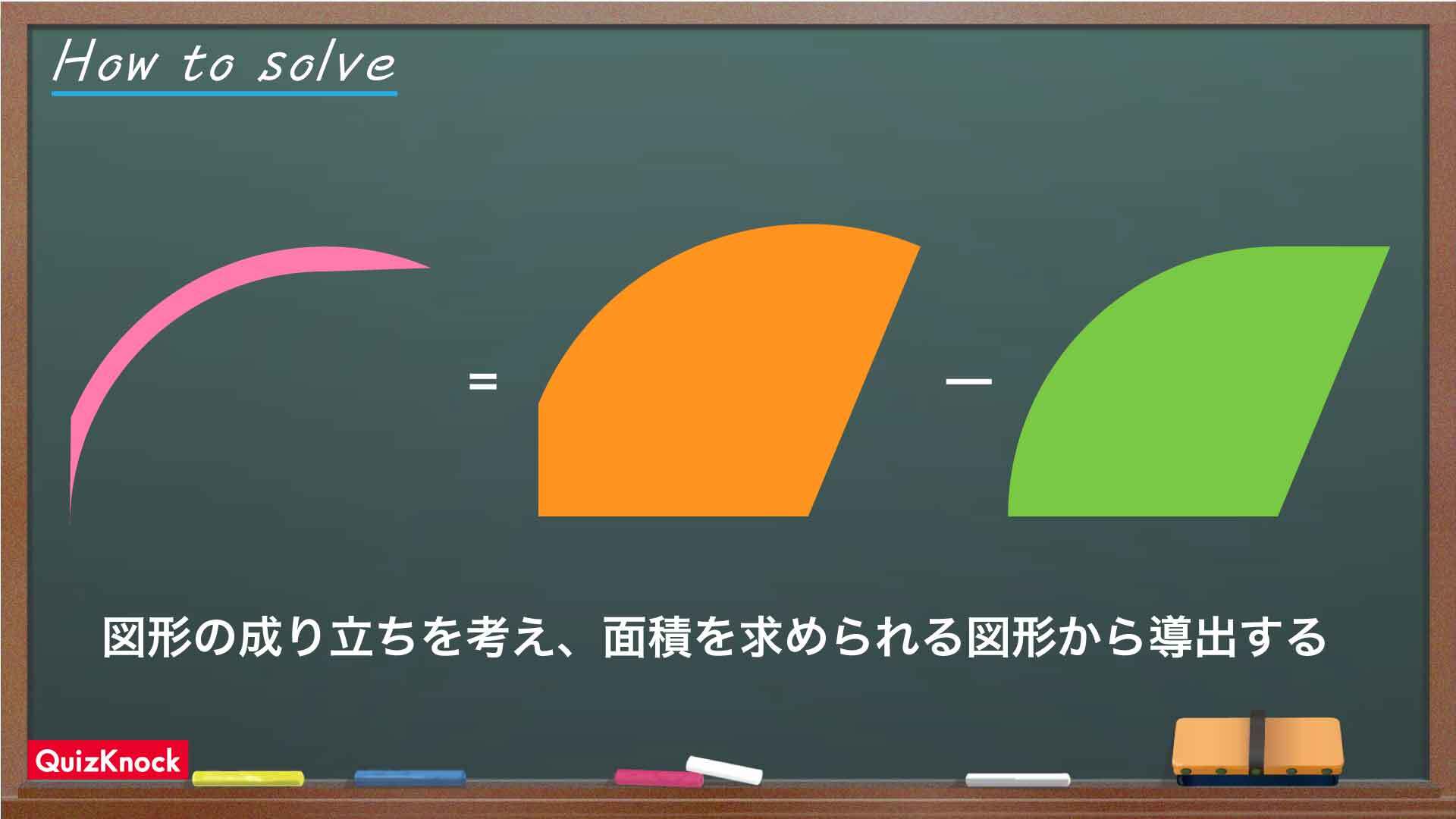
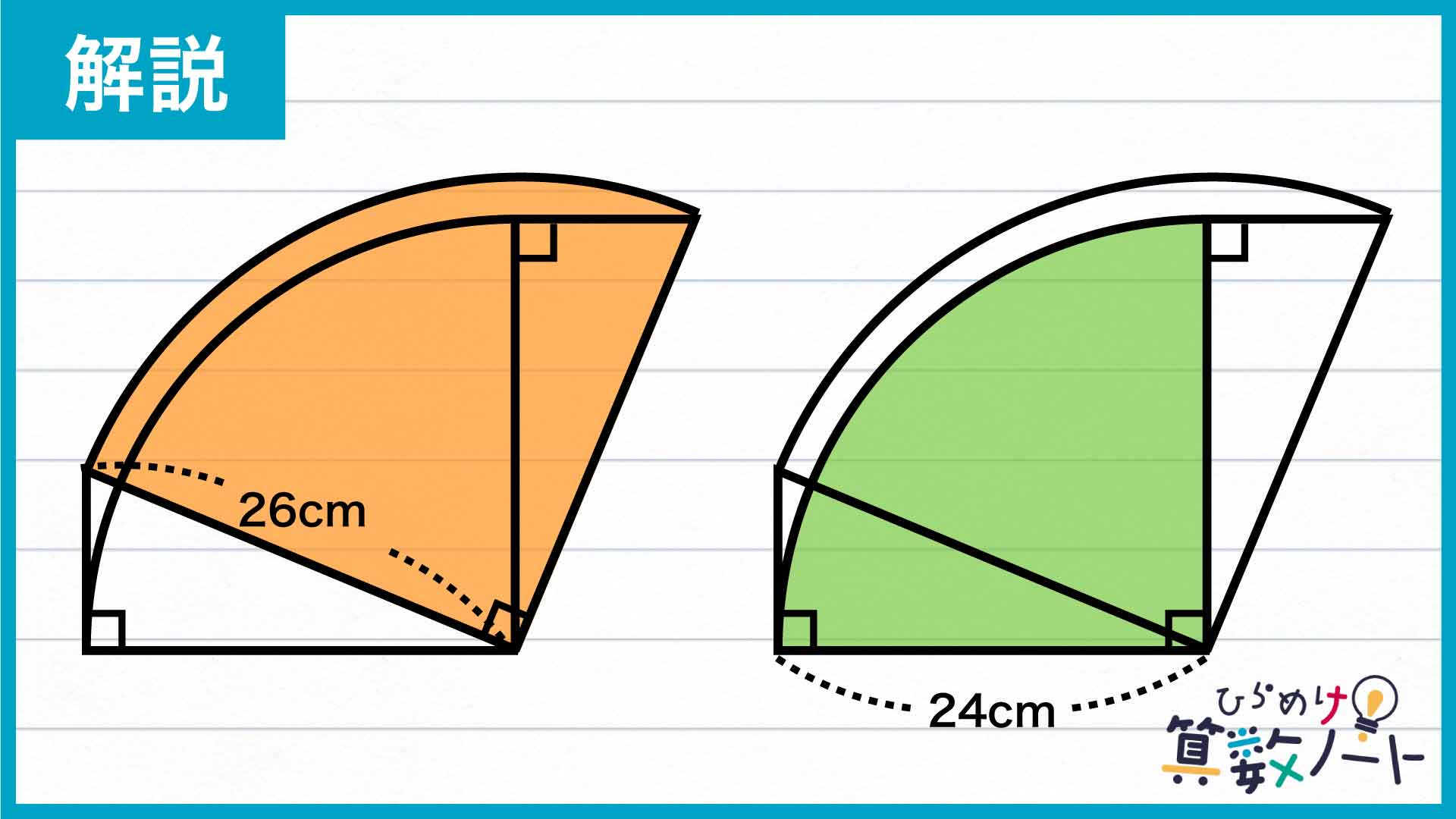
半径26cmの扇形を回転前の三角形と、半径24cmの扇形を回転後の三角形とそれぞれ組み合わせると、下の図のようなオレンジ色と緑色の図形になります。
すると、ピンク色に塗られた図形は、オレンジ色の図形から緑色の図形を引いて余った部分であることがわかります。
したがって、オレンジ色の図形と緑色の図形それぞれの面積がわかれば、ピンク色の図形の面積を求めることができます。
ピンク色に塗られた図形の面積を求める
以上より、ピンク色に塗られた図形の面積は以下のように求められます。
(オレンジ色の図形の面積)-(緑色の図形の面積)
=(26×26×π÷4+三角形の面積)-(24×24×π÷4+三角形の面積)
=(26×26×π÷4)-(24×24×π÷4)
=25πcm2
答え:25πcm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)