解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
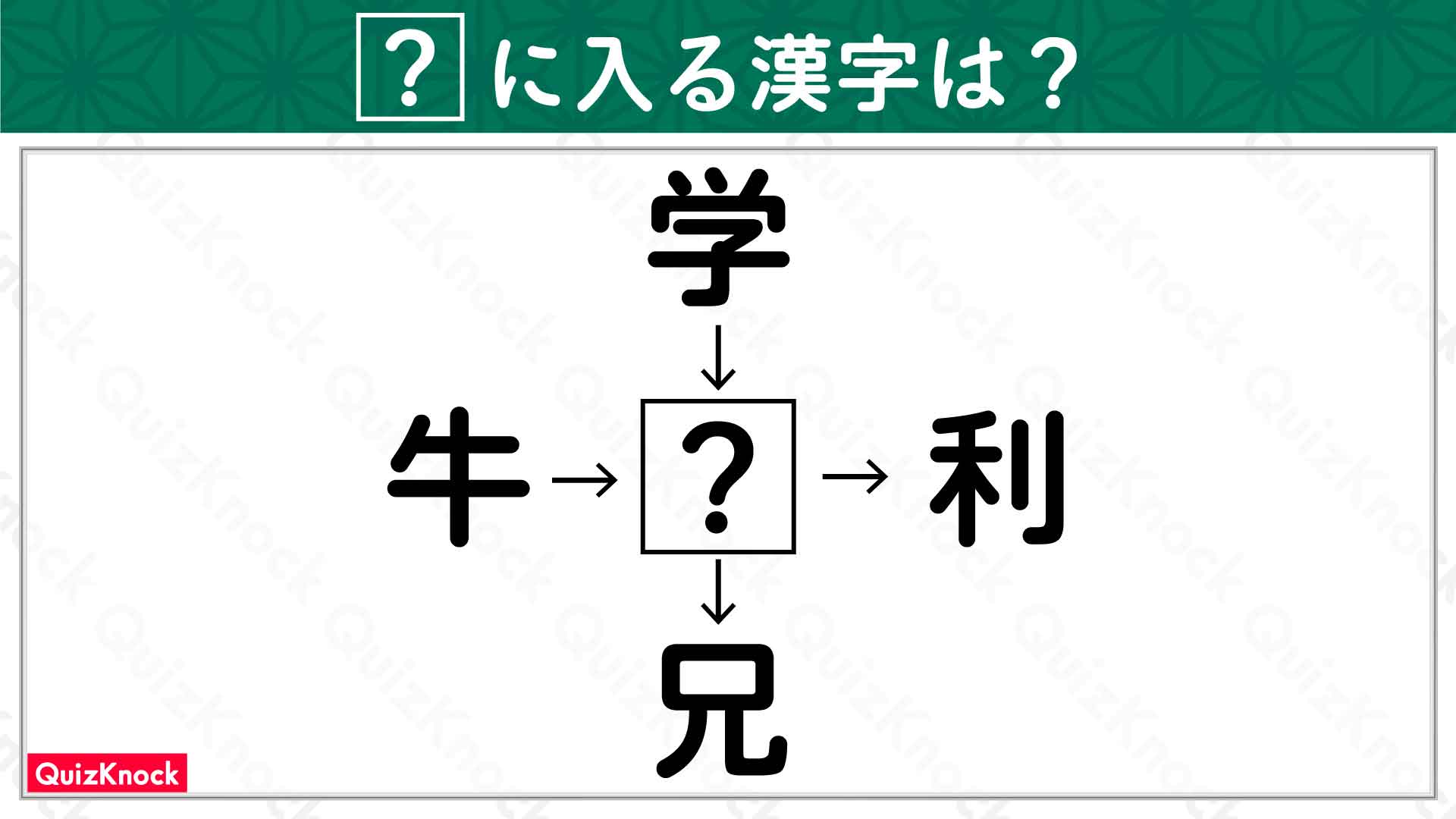
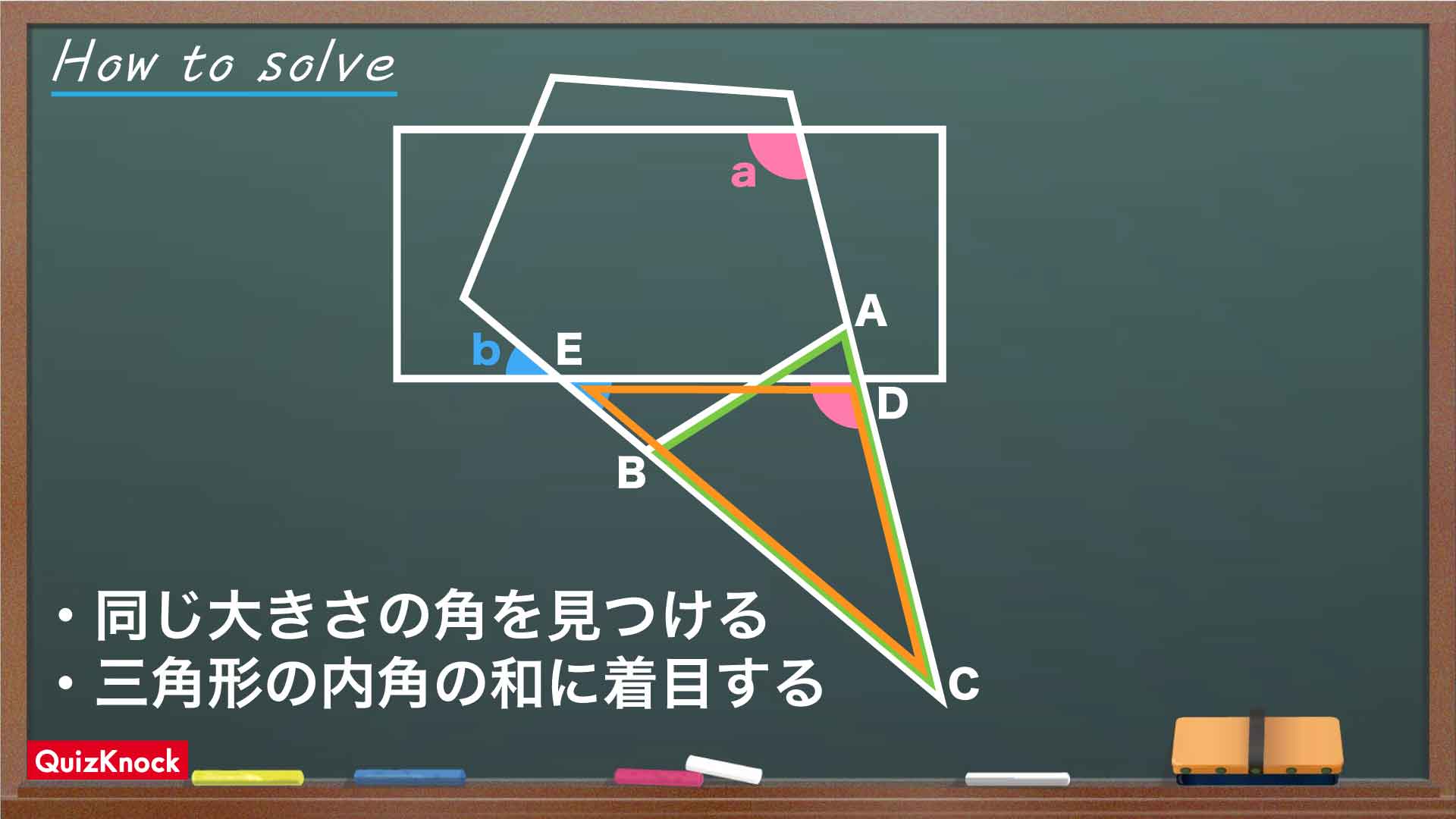
今回の問題の解き方をまとめた図がこちらです。ポイントは同じ大きさの角を見つけ、三角形の内角の和に着目することです。
このポイントをもとに、解いていきましょう!
補助線を引き、角度を求める
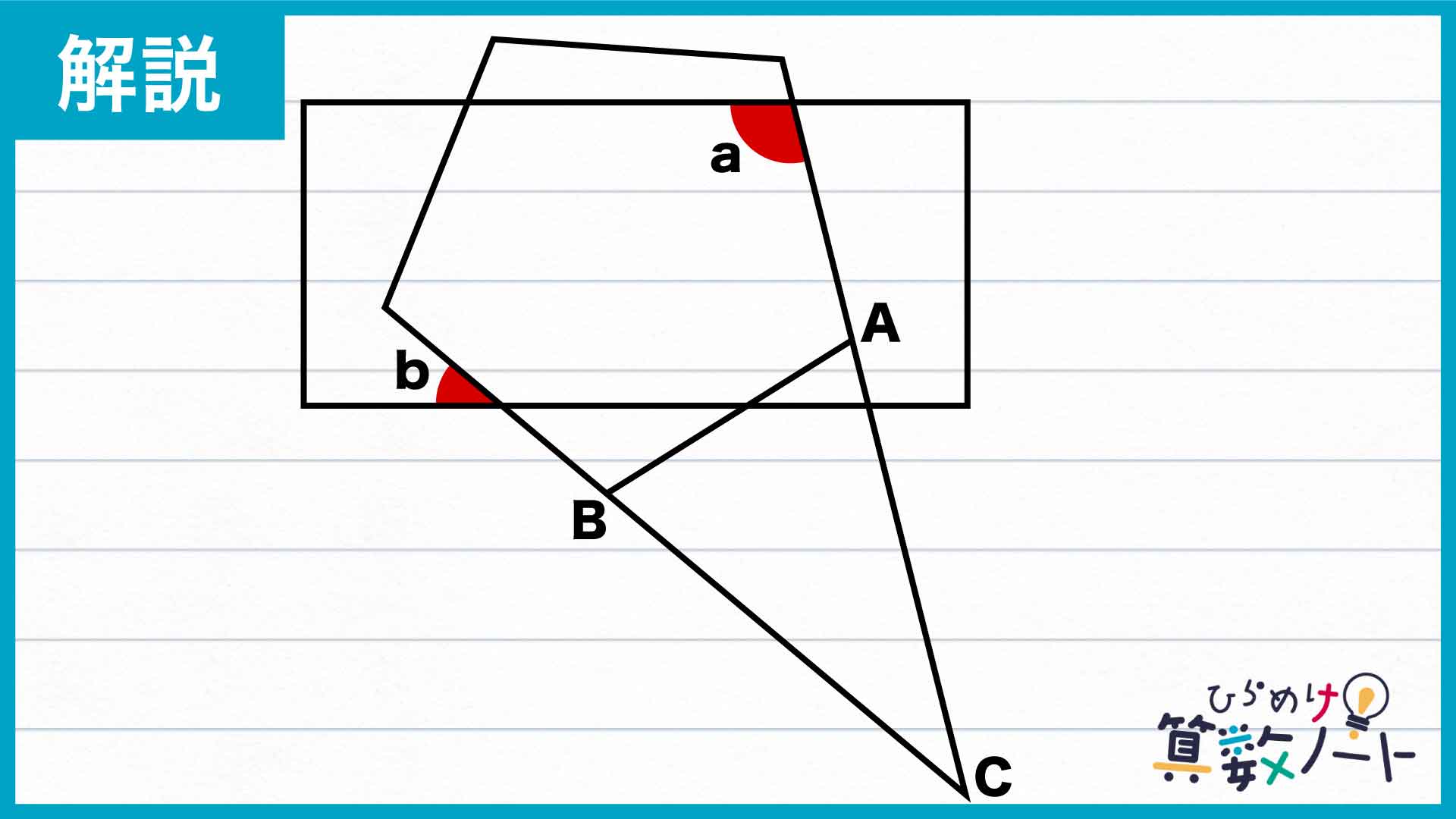
まずは、下の図のように正五角形の2つの辺を延長する補助線を引き、三角形ABCを作ります。
次に、三角形ABCの3つの内角の大きさを求めていきます。
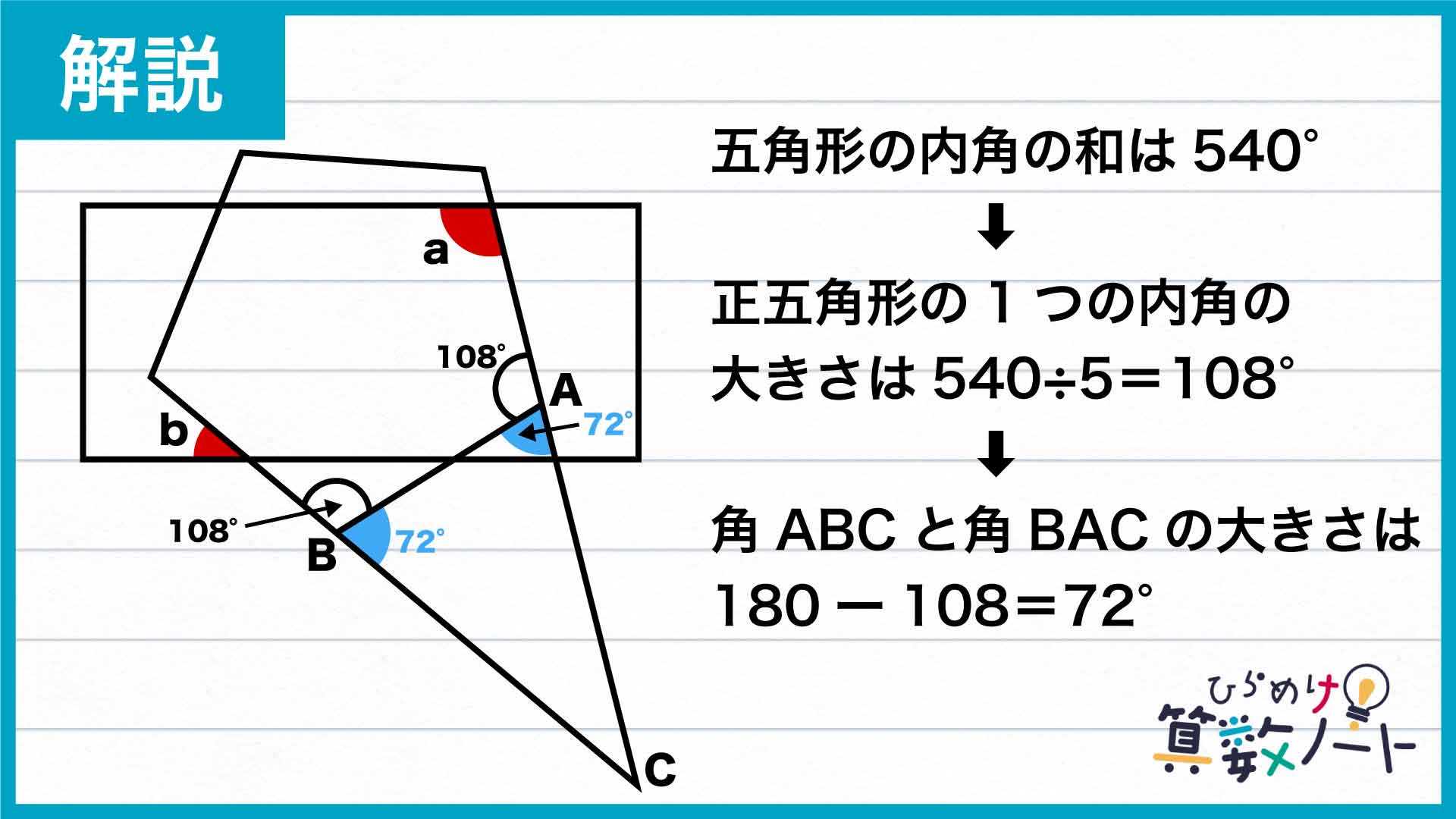
五角形の内角の和が540度であることから、正五角形の1つの内角は540÷5=108度です。
角ABCと角BACはいずれも正五角形の外角なので、角ABC=角BAC=180-108=72度となります。
三角形ABCの内角の和は180度であることから、角ACB=180-72×2=36度です。
角a、角bと同じ大きさの角は?
角aと角bの和を求めるために、角a、角bと同じ大きさの角を探しましょう。
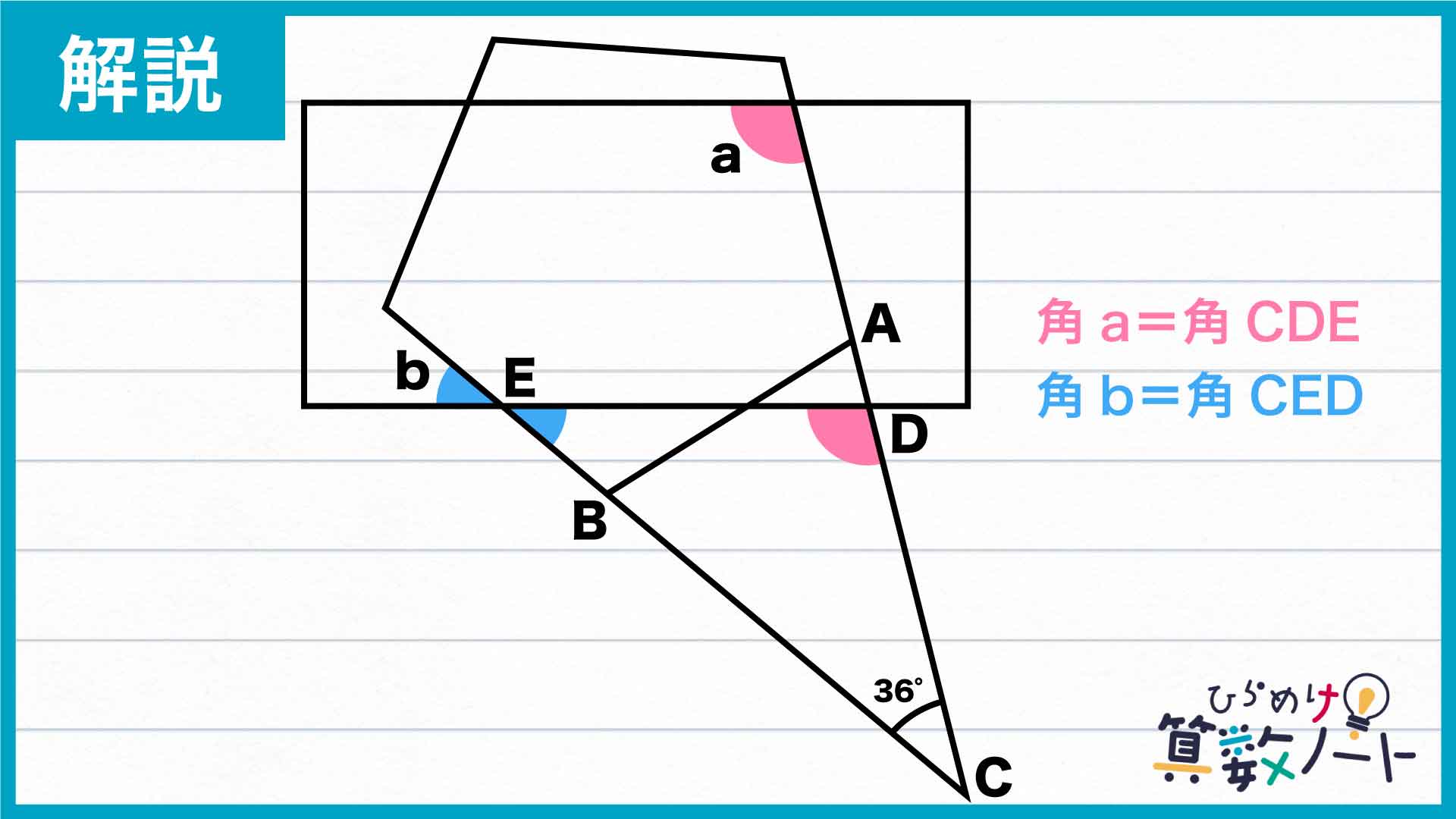
ここで、下の図のように直線ACと長方形の辺の交点を点D、直線BCと長方形の辺の交点を点Eとします。
まずは、角aと同じ大きさの角を探します。
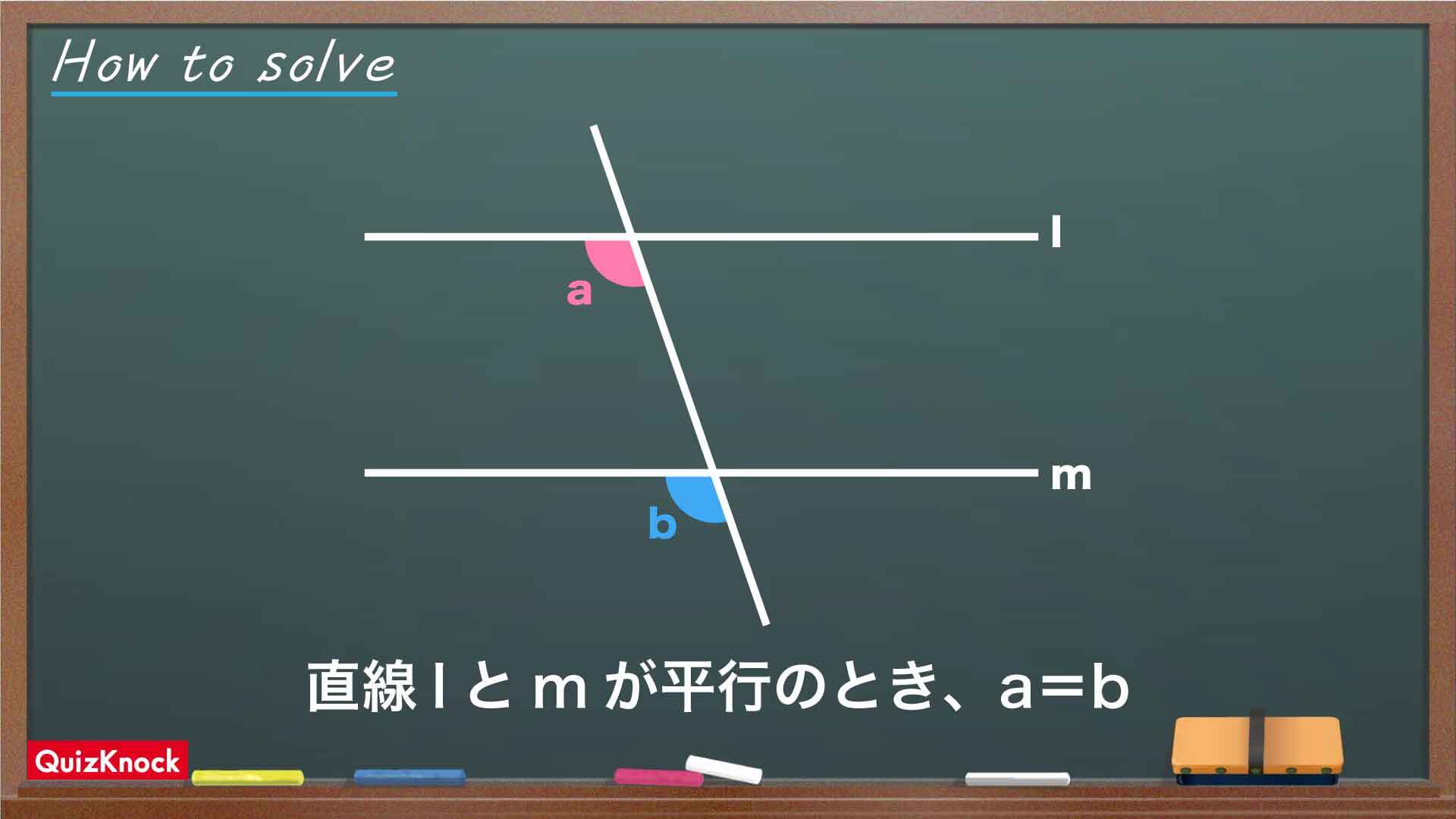
長方形の向かい合う辺はそれぞれ平行です。2本の平行線に1本の直線が交わるとき、下の図のような関係にある角の大きさは等しくなるという性質があります。
このことから、角a=角CDEであることがわかります。
次に、角bと同じ大きさの角を探します。
角bは角CEDと向かい合う関係にあります。2直線が交わってできる角のうち、向かい合う角の大きさは等しいという性質があります。したがって、角b=角CEDとなります。
最後は三角形CDEに注目!
角aと角bの和は、角CDEと角CEDの和と等しいことがわかりました。
そこで三角形CDEに着目すると、内角の和は180度、角DCE=36度であることがわかっています。
したがって、角CDE+角CED=180-36=144度となります。
角aと角bの和は、角CDEと角CEDの和と等しいことから、角a+角b=144度です。
答え:144度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】














.jpg)









.jpg)