解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
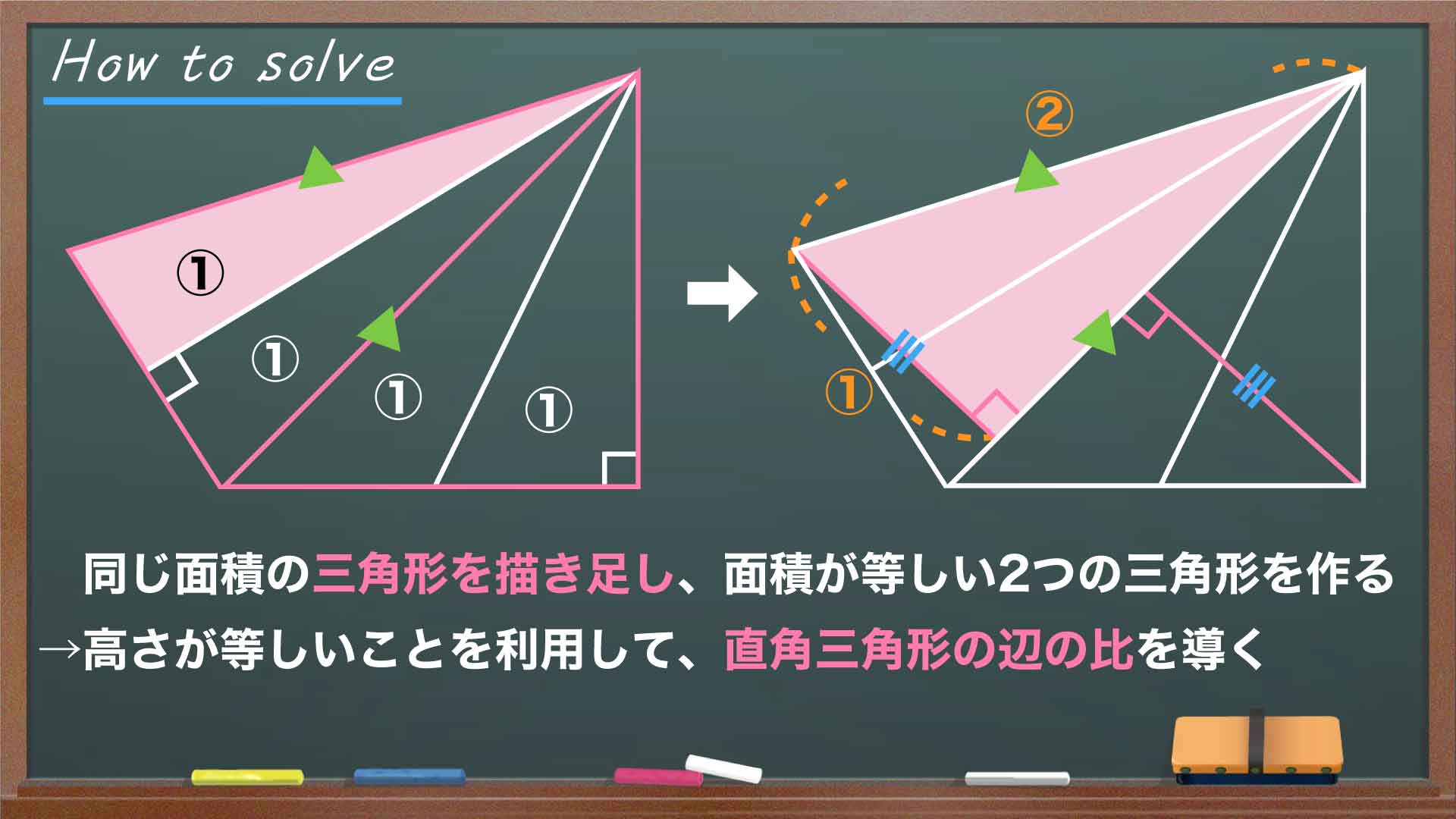
問題の解き方をまとめた図がこちらです。
ポイントは、補助線や新たな図形を描き足しつつ、辺の長さと面積との関係をうまく利用することです。
では、このポイントを踏まえつつ解いていきましょう!
長さの等しい辺から三角形の面積比を導く
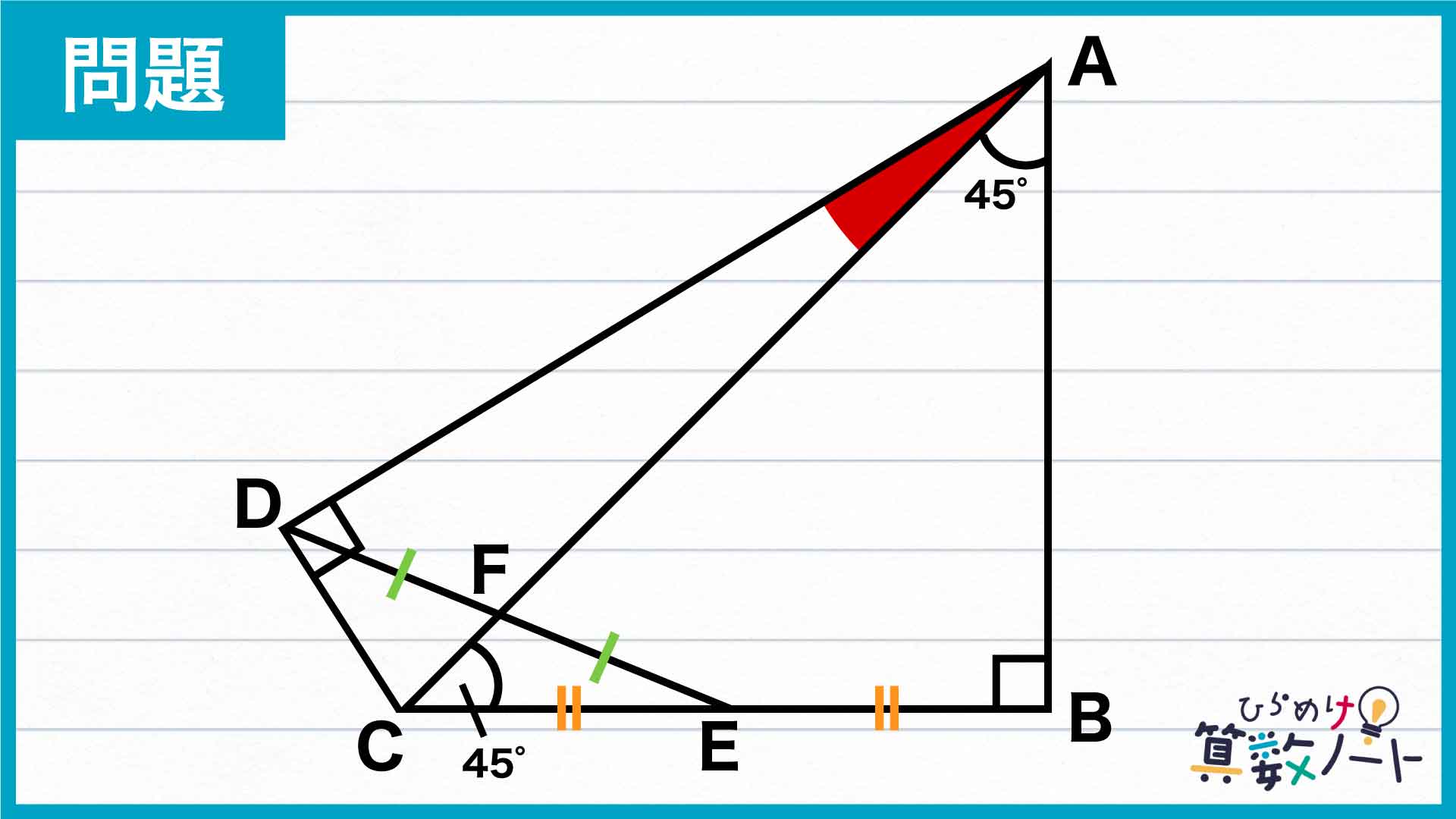
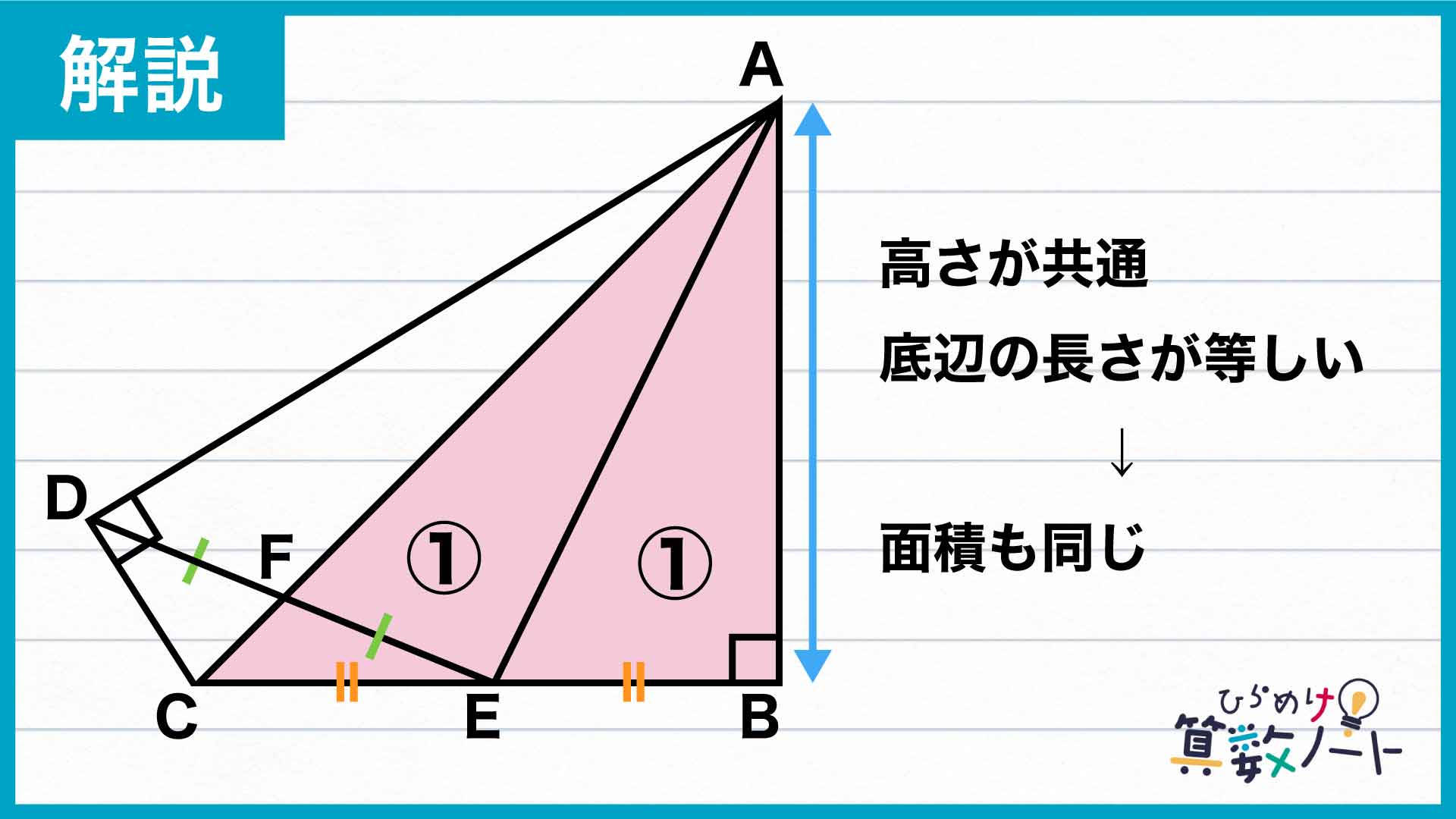
長さが等しいとわかっている部分を利用するために、補助線AEを引いてみましょう。そして、三角形ACEと三角形ABEに注目します。
ここで、辺CEと辺BEが同じ直線上にあり、かつ頂点Aが共通していることから、辺CE、辺BEをそれぞれ底辺としたときの高さは等しくなります(今回は直角三角形なので、ちょうど辺ABの長さにあたります)。さらにCE、BEの長さは等しいので、三角形ACEと三角形ABEの面積は等しいことがわかりました。
続いて、三角形ADFと三角形AEFに注目してみましょう。この2つについても同じように考えると、底辺DF、EFの長さが等しく高さも共通していることから、やはり面積は同じになります。同様のことが、三角形CDFと三角形CEFについてもいえます。
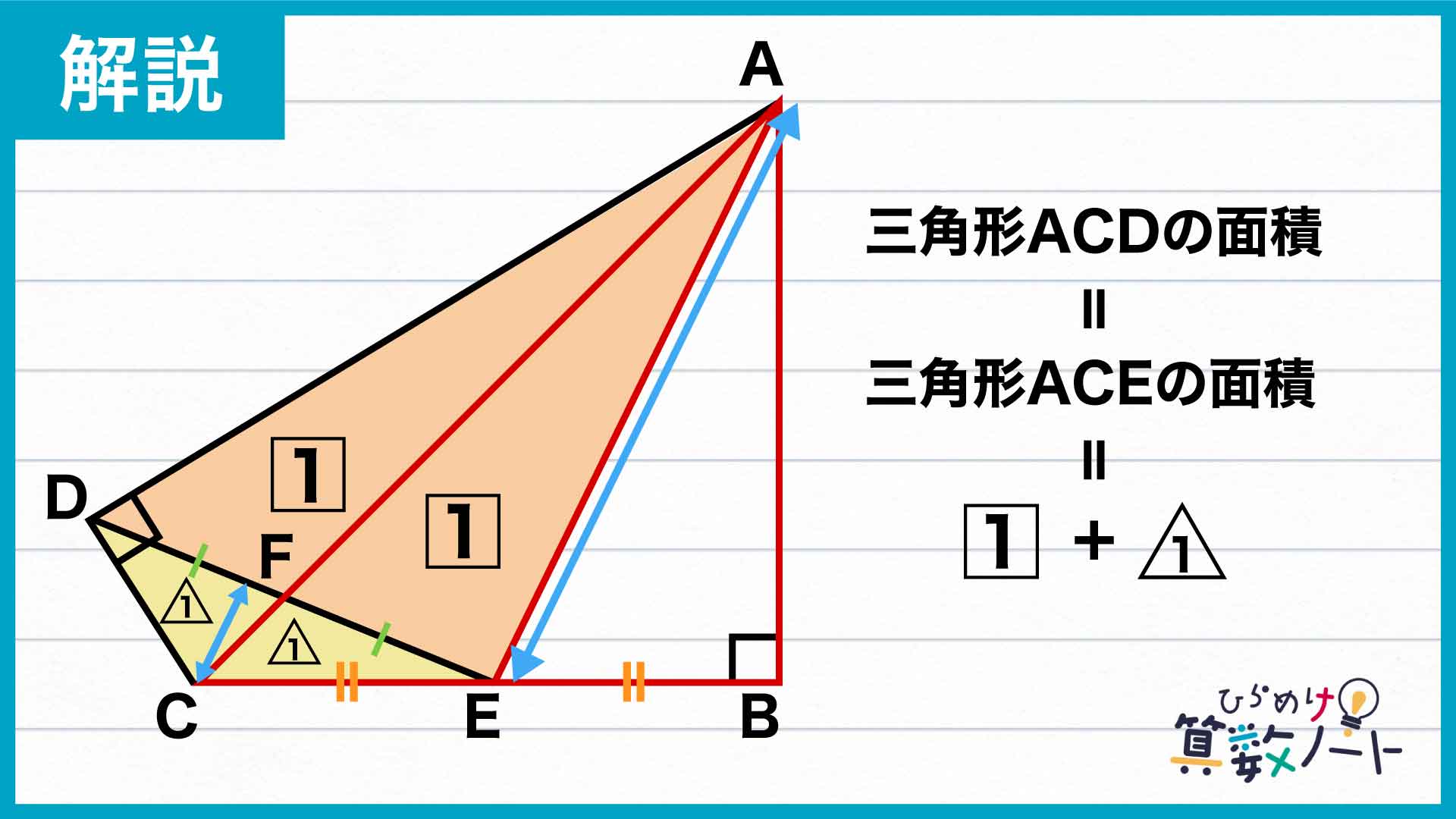
よって、これらの三角形を一つずつ組み合わせてできた三角形ACDと三角形ACEの面積もまた、等しくなるのです。
結局、三角形ABE、三角形ACE、三角形ACDの面積は全て等しかったということがわかります。では三角形ABCと三角形ADCの面積比はというと、図より(1+1):1=2:1となります。
面積の等しい三角形を作る
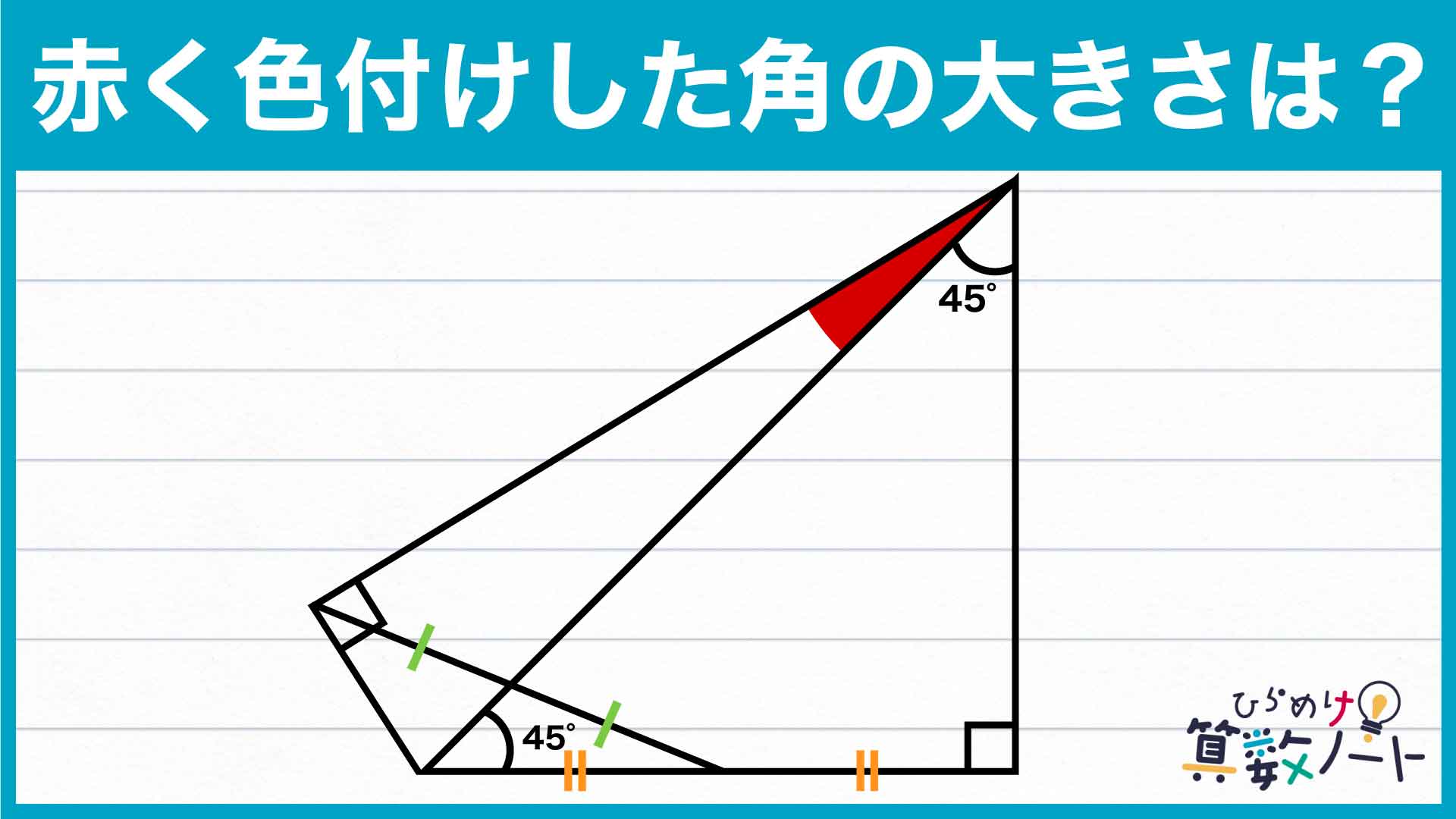
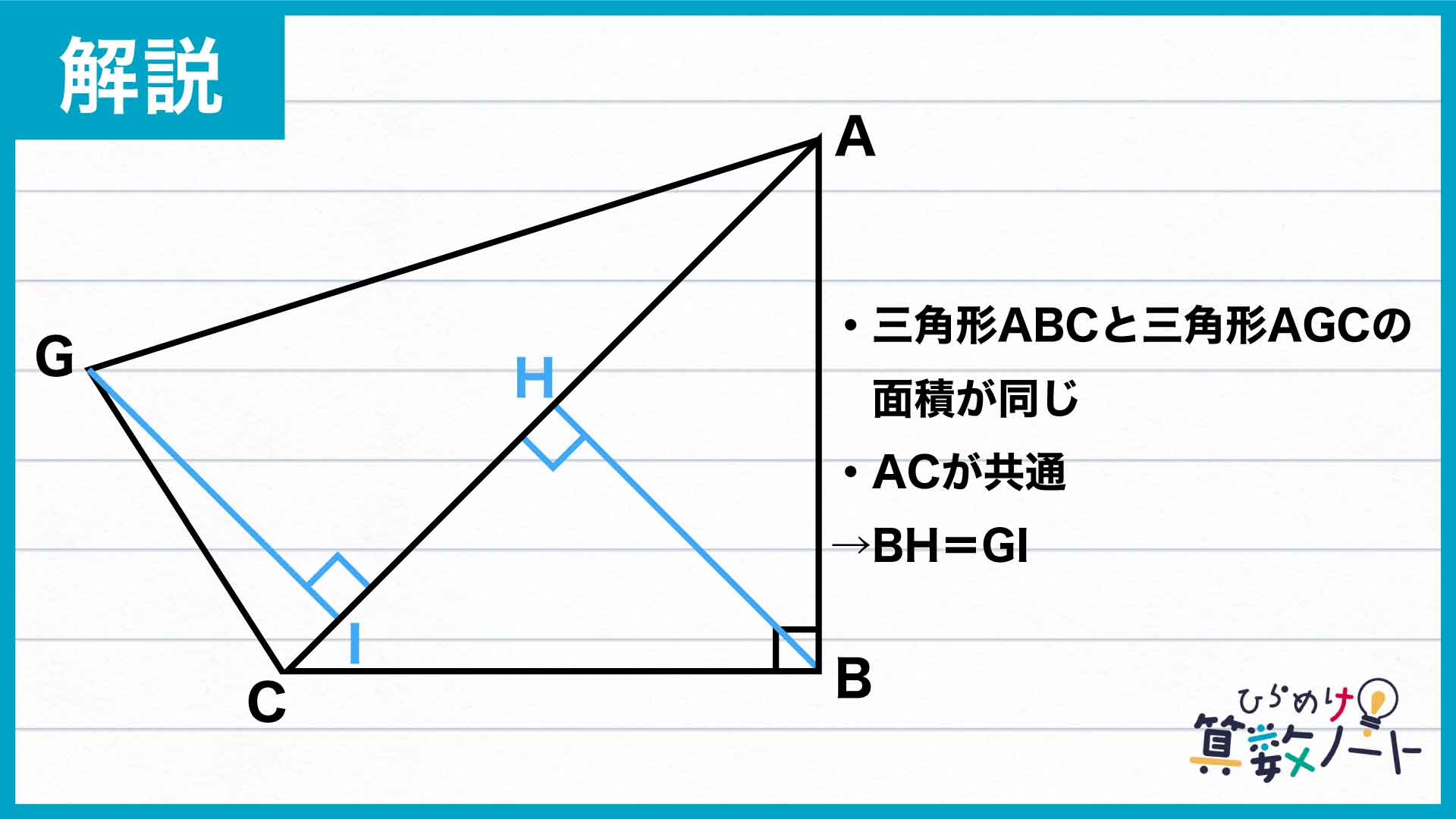
三角形の面積比がわかったところで、もう一つの「工夫」です。面積の等しい三角形を作るために、三角形ADCと合同な三角形ADGを図のようにくっつけてみましょう。すると、三角形ABCと面積が等しく、AC=AGである二等辺三角形AGCができました。角CAGは、求める角CADのちょうど2倍の大きさになります。
2つの三角形に共通する辺ACをそれぞれの底辺とすると、面積が等しいことから高さも同じになります。つまり、頂点B、頂点Gからそれぞれ辺ACへ垂直に引いた線分BH、GIの長さが等しくなるのです。
辺の比から角度を求める
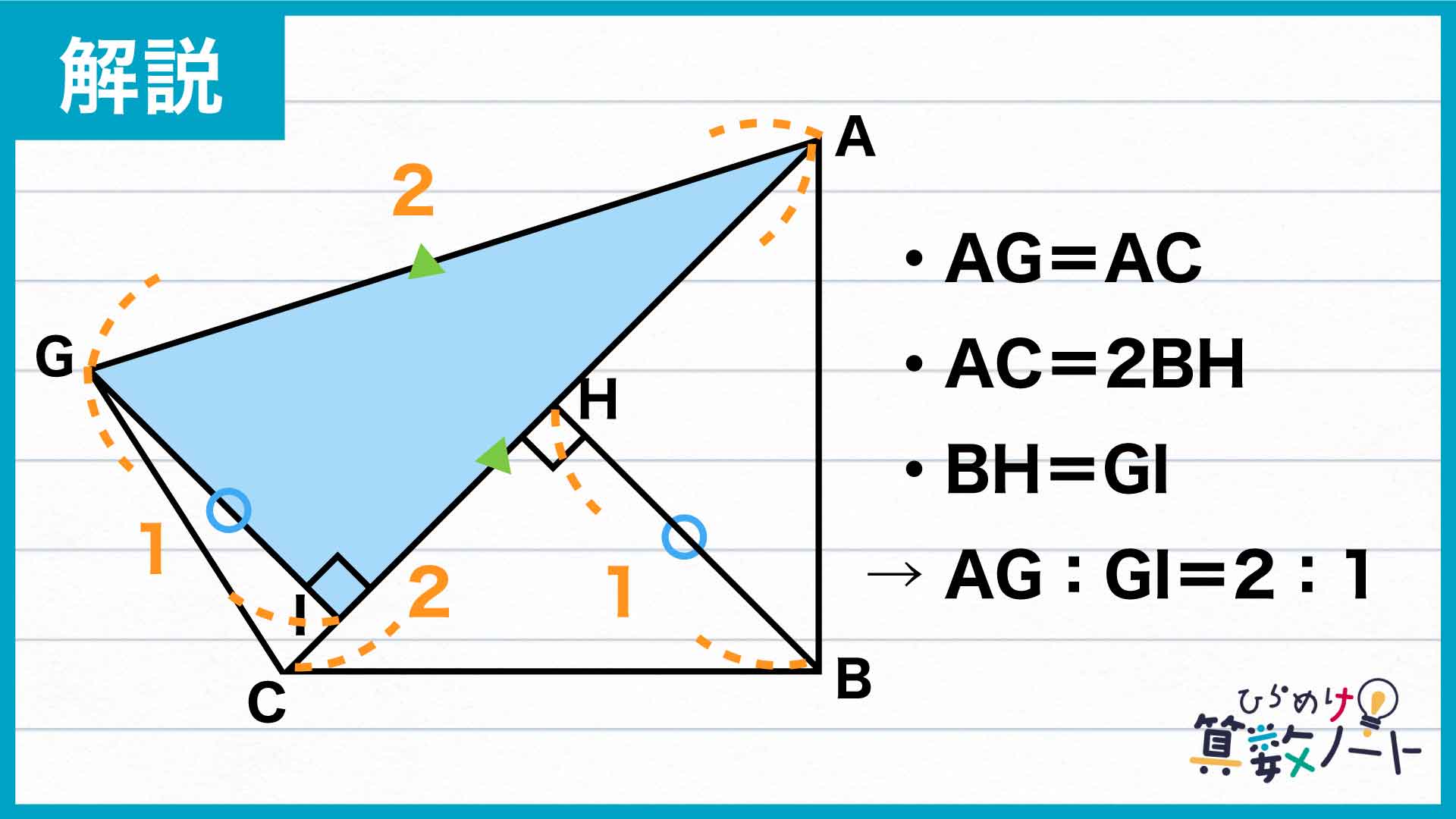
問題にある通り、三角形ABCは直角二等辺三角形です。よって、直角三角形ABHにおいて角BAHは45度であり、この三角形もまた直角二等辺三角形だとわかります。同様に考えると三角形CBHも直角二等辺三角形であり、結果AH、BH、CHの3つの辺は全て長さが等しくなります。よって、ACの長さはBHのちょうど2倍になることがわかりました。

今度は三角形AGCに注目です。三角形AGCはAC=AGの二等辺三角形であり、またBHとGIの長さが等しいことから、先ほど導いた長さの比を使ってAG:GI=AC:BH=2:1であるとわかります。よって三角形AGIは、AG:GI=2:1、角AIG=90度の直角三角形です。
この三角形AGIの形、見覚えありませんか? そうです、三角定規の形としてもお馴染みの、正三角形を半分にした直角三角形と同じなのです。この三角形は直角を除く残りの内角の大きさが30度、60度であることも知られており、このことから角GAIの大きさは30度だとわかりました。
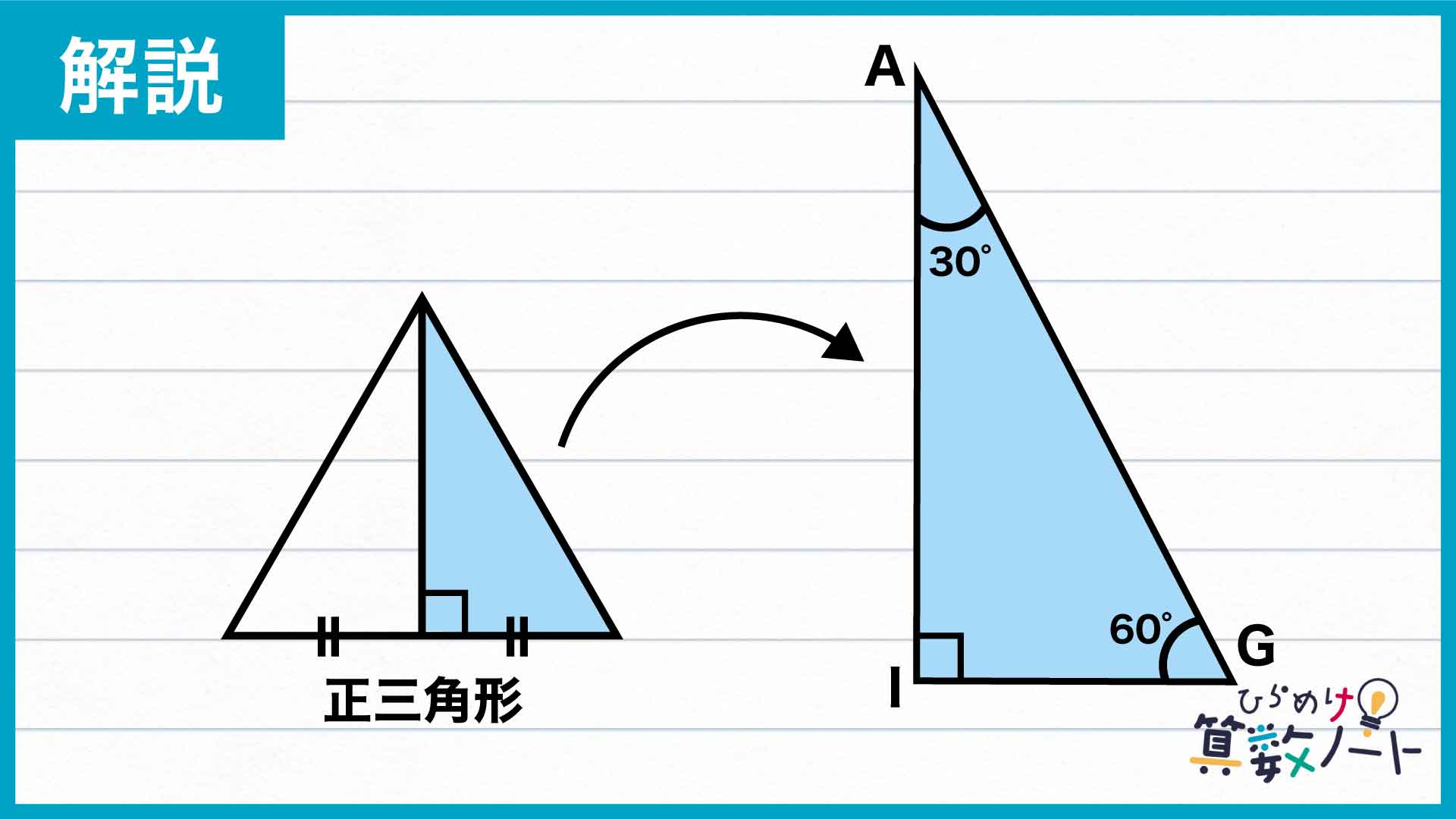
角GAIは、大きさの等しい角CADと角GADがくっついてできたものでした。したがって、求める角CADの大きさは30÷2=15度であるとわかるのです。
答え:15度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)








.jpg)







