みなさんは「ベイズ統計」を知っていますか? 書店に行くと「ベイズ統計」の本は何冊も置いてあるのでご存知かもしれません。
たくさんの本が出版されている通り、ベイズ統計は多くの分野に使われています。 何やら友好的でない響きのベイズ統計ですが、実はみなさんの日常の中にもその考え方は活用されています。 有名な例だと、迷惑メールの振り分けにはベイズ統計が使われています(これは後に詳しく解説します)。
この記事では、意外と役立つ日陰者・ベイズ統計について、簡単に説明してみようと思います。
まずは、こちらの画像をなんとなく見てください。
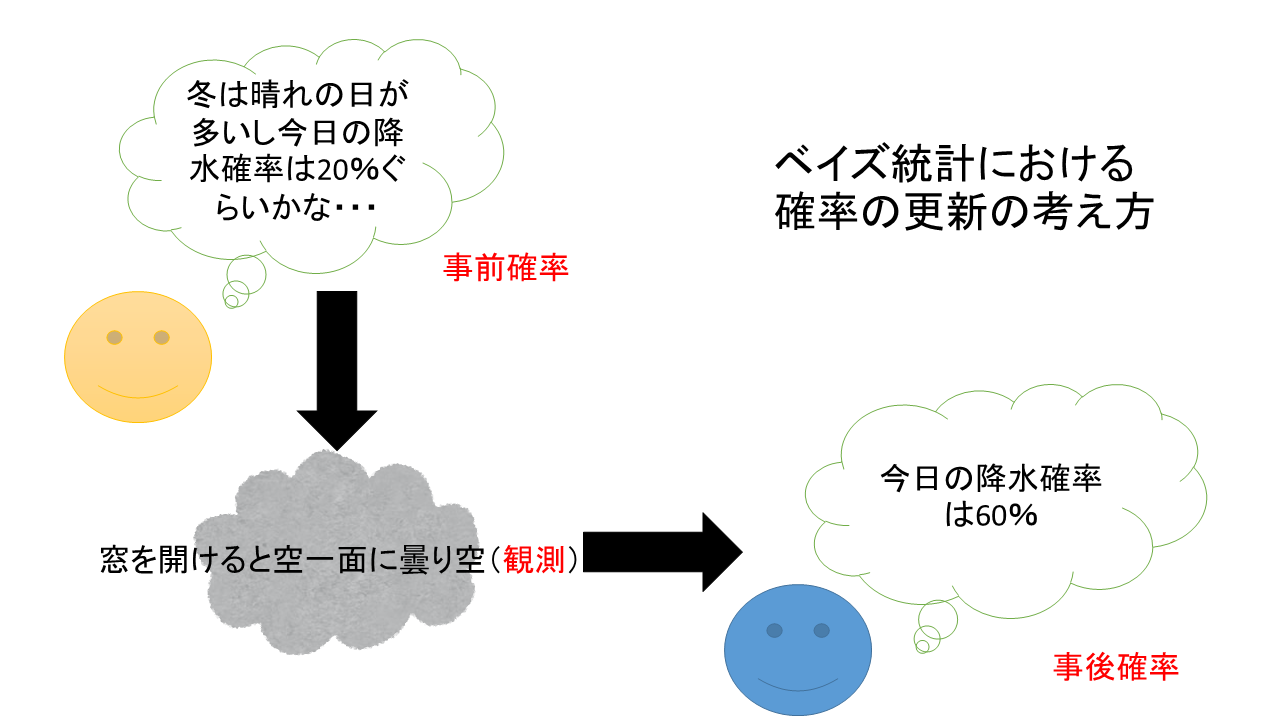
出てくる用語等はあとから徐々に解説するとして、ぼんやりと「こういう流れの考え方を使うんだなー」と把握しておいてください。
さて、ベイズ統計は統計学の「流派」みたいなものです。普通の統計学(これを比較のために頻度主義と呼びます)に対してベイズ統計学があるというイメージです。両者の違いは何でしょうか? まずは次の問題を考えてみてください。数式が苦手な人はサラッと流してかまいません。
このように 得られた結果(表が2回、裏が1回出たというデータ)から 原因(どのようなコインを使ったか)を推測する のが、ベイズ統計の考え方です。
しかし、頻度主義の統計学ではこうは考えません。 コインを投げてデータを得る以前から「このコインを投げたとき表と裏がどれくらいの確率で出るか(=確率分布)」は決まっており、実験して得られたデータは多数の可能性の中から確率分布にしたがって1つが現れた結果であるという考え方をとります。原因と結果の関係が逆ですね。
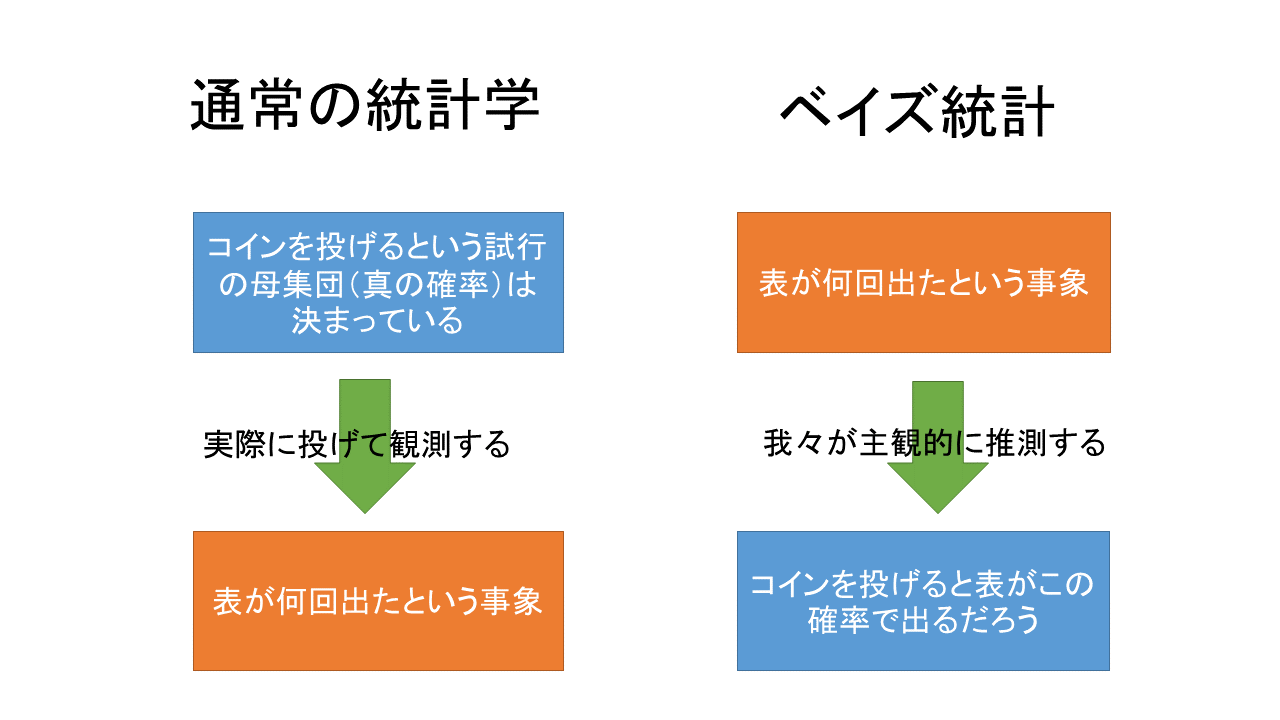
ベイズ統計では、データを得ることで確率が変化すると考えます。つまり、
(事後確率)=(事前確率)×(データを得たことによる修正項)
と考えるわけです。 データを得る前は何も情報がないのですから表が出やすいコインを使っている確率(事前確率)は1/2と主観的に考えます。(これを理由不十分の定理といいます。よくわからんから1/2にしてしまおうという考え方は、頻度主義的な統計学ではありえないことです。) 実際にコインを投げてみて表2回、裏1回というデータを得ると、表が出やすいコインを使っている確率(事後確率)は67%に更新されます。
といったところで、冒頭の画像をもう一度見てみましょう。数式では何のことやら……という人も、直観として理解できればOKです!

ベイズ統計の強みは、データを得る前から持っている我々の事前知識を確率に組み込めることです。とくにデータが少ない時は、われわれの事前知識は非常に有効になります。しかし一方で、「観測できないものは科学とは呼べない」という立場に立てばベイズ統計を認めることはできなくなります。
ベイズ統計が実際の生活に使われている有名な例として、前述した迷惑メールのフィルタリングがあります。
 迷惑メールは迷惑だなあ
迷惑メールは迷惑だなあフィルターは「URLが貼られている」「出会いという言葉が使われている」など迷惑メールにありがちな特徴をもとにメールを分析し、メールが迷惑メールかを判定します。
ある1通のメールが届きました。開封する前は迷惑メールかどうかは分からないので、理由不十分の定理より迷惑メールである確率は50%にしておきましょう。 次にフィルターがメールを読んでいきます。「出会い」という言葉を見つけました。条件付確率にしたがって確率を更新した結果70%になりました。 さらに、このメールにURLが貼ってあることが分かりました。迷惑メールである確率は80%になりました。 こういった作業を繰り返し、迷惑メールである確率が一定値を超えたら迷惑メールフォルダ行きです。
もちろん求めているのはあくまで確率ですから、間違えることはあります。大事なメールが迷惑メールに振り分けられていたという経験は誰しもあるでしょう。
他にも画像認識や人工知能など、ベイズ統計はあらゆるところに利用されています。 この記事ではカンタンにしか説明しませんでしたが、ベイズ統計は面白いと思っていただけたら幸いです。










.jpg)

















