こんにちは、セチです。
今年の夏は特に暑い日が続いていますが、暑さにやられて普段はしないような判断ミスをしてしまうこと、ないでしょうか？
「山より海に行くんだった」とか「告白するのは今じゃなかった」とか――「別の宝くじにしておけば良かった」とか。ちょっと強引な導入ですが、今回はそんな「宝くじ」に関するお話です。
一口に「宝くじ」と言っても、日本にはいろいろな種類があり、どれを買えば良いかわからなくなることもあるかと思います。そこで、高校数学でも学習する「期待値」の考え方を使って、「宝くじ1枚でいくら儲けられるか？」ということを考えたいと思います。
「期待値」とは？
そもそも「期待値」とは何なのかというと、「ある確率変数が平均してどのような値をとるか」を示す値であると言えます。ちょっとわかりにくいので、身近な例として「サイコロの目の期待値」を挙げます。
サイコロの6面がそれぞれ同じ確率（＝6分の1）で出るとすると、出る目の値の平均は1/6×1+1/6×2+1/6×3+1/6×4+1/6×5+1/6×6=3.5となり、サイコロの目の期待値は3.5と求められます。
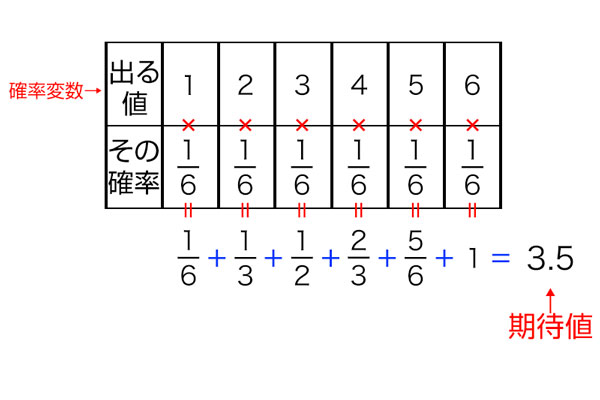
サイコロの目のような、ランダムに変化する値を「確率変数」と呼び、確率変数がとる値とそうなる確率の積を足し合わせていくと、得られる結果の平均すなわち期待値が求められるというわけです。
定番！ ジャンボ宝くじ
さて、ここからが本題。確率変数を「宝くじ1枚で得られる金額」とすると、その期待値がもらえる金額の期待値。これを知り、買うべき宝くじを正確に判断したいところです。
まずは、定番とも言うべきジャンボ宝くじについて。
一般に言われる「5大ジャンボ」とは、当せん金が高額な5つの宝くじの総称です。「バレンタインジャンボ（2月）」「ドリームジャンボ（5月）」「サマージャンボ（8月）」「ハロウィンジャンボ（10月）」「年末ジャンボ（12月）」を指します。基本的には1枚300円で買うことが出来ます。
直近にあった2018年のサマージャンボ。1等の5億円に当たる確率は0.00001%と微々たるものですが、6等300円まで行くと10％となかなかのものです。
これらの「金額×確率」の値を足していくと、期待値はおよそ141円。他のジャンボ宝くじや、同時発売の「ジャンボ宝くじミニ（最高額が低め）」も概ね同じ値が出ましたが、年末ジャンボはもう少し高く、昨年（2017年）末で約150円の期待値。ジャンボ宝くじを狙うなら年末でしょうか。
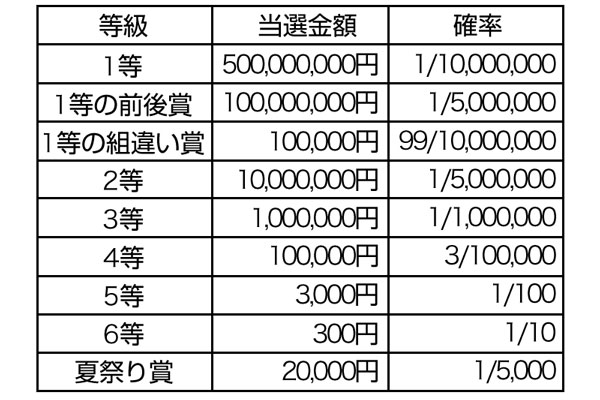2018年のサマージャンボの各等の当せん確率スクラッチの場合
では、逆にチャンスが多いスクラッチではどうか。
スクラッチはいつでも発売されており、その場で当たり外れがわかるのが特徴です。回によってまちまちですが、今年（2018年）8月の「ドラゴンボールスクラッチ 魔人ブウ ラッキートライアル」は最高1000万円と、ジャンボ宝くじよりは低額ですが、その分当たりそうな気がしてきます。
先ほど同様、各等の「金額×確率」を足して計算すると、「魔人ブウ ラッキートライアル」の期待値は90円となりました。1枚が200円のため、割合にすると45％。300円のものもありますが、どれも価格の45％程度の期待値であり、ジャンボ宝くじよりは低くなっています。
数字選択式宝くじの場合
続いては数字選択式宝くじを見てみましょう。この中には、「ロト6」「ロト7」「ミニロト」や、「ナンバーズ」「ビンゴ5」という、読んで字のごとく数字を選んで買う宝くじが含まれます。
数字選択式宝くじは共通してパリミュチュエル方式という配当方式を採用しています。これは、総売上の一定割合が配当に回され、各等ごとに決められた配当率で割り振られ、その額を同じ等級の当たりくじに等分するというものです。結果として、同じ等級で当たった人が多いほど取り分は少なくなります。
つまり、
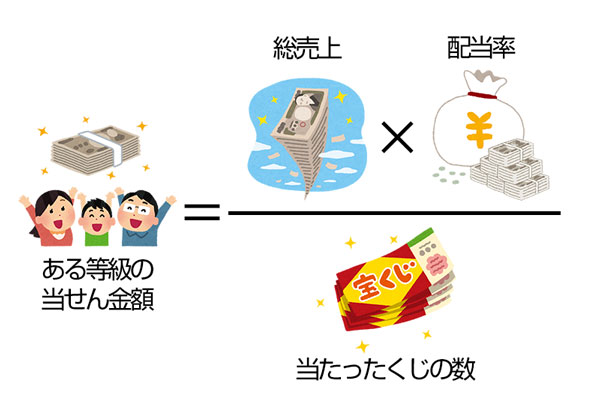
のようになります。
また理論上、ある等級に当たる確率は数学的に求められます。たとえば、ロト7の1等は37の数から7つの本数字を引かなければならないので、7C7/37C7=1/10295472となります（今回は細かいことはわからなくても大丈夫です）。そして、これをもとに「当たると考えられるくじの数」を求めると、
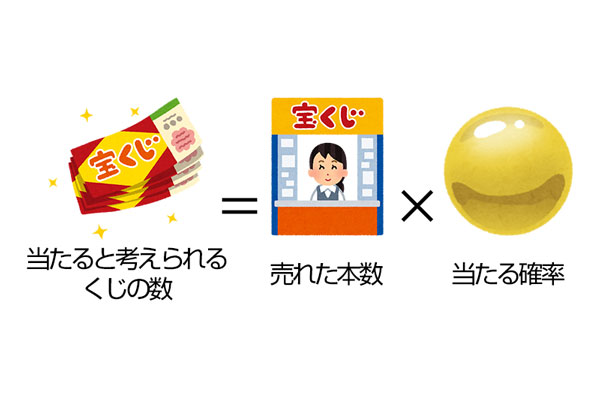
となります。また、「売れた本数」は「総売上」を「1枚の価格」で割ると求められるので、
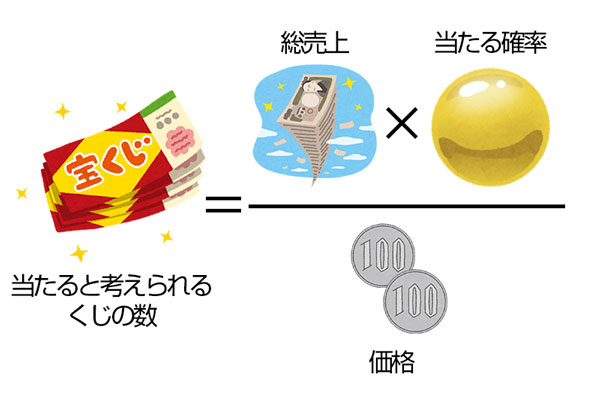
と表せ、これを1つめの式に当てはめることで「理論上の当せん金額」が求められ、
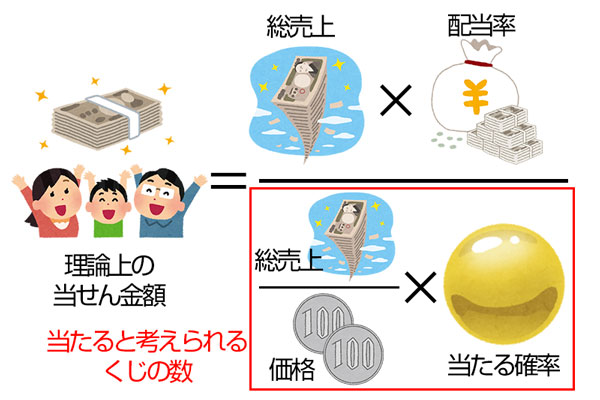
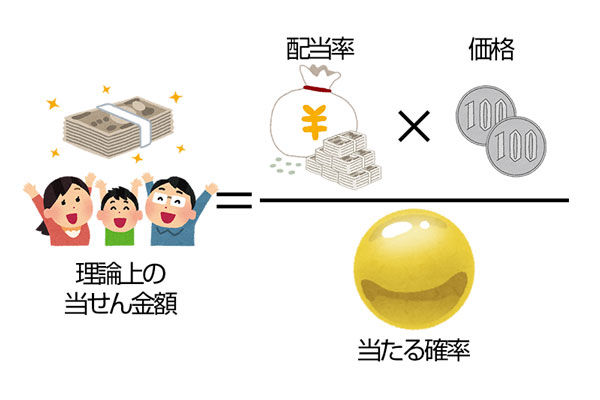
となります。そして、期待値は（当せん金額）×（当たる確率）の和で求められるので、
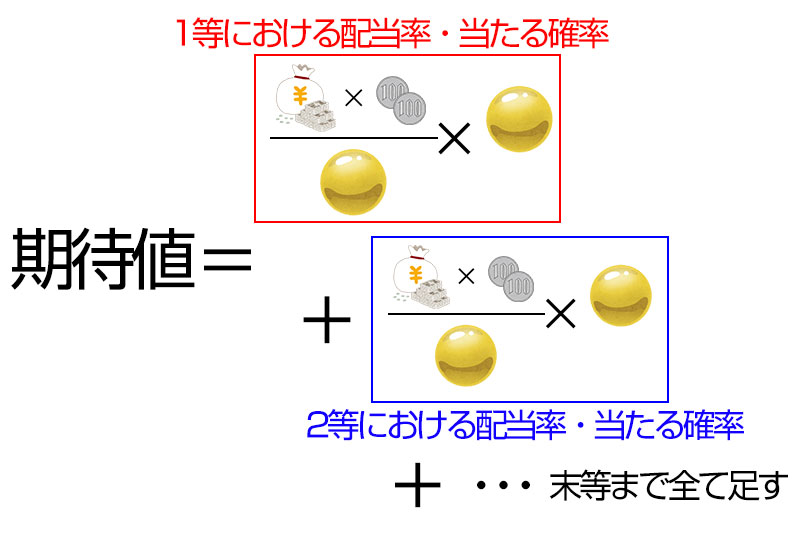
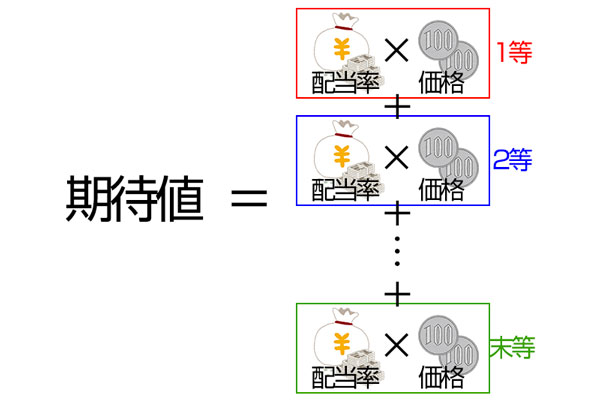
というように表せます。また、同じくじなら価格は同じで、数字選択式宝くじの配当率は各等合計して45％と決まっているので、期待値は原則どれを選んでも価格の45％です（実際の当せん金額は、100円未満が切り捨てられるので若干ブレますが）。
ジャンボ宝くじの期待値が150円（価格の50％）弱ということを考えると、「ジャンボ宝くじの方が良いんじゃ？」という結論になりそうですが……
キャリーオーバーがあるときは、期待値が上がる
ロト6とロト7には「キャリーオーバー」という制度があります。これは、1等の当たりが出なかった場合に次回にその分の金額を繰り越す制度で、繰越金額は次の1等に上乗せされます。
ここで注目すべきは、キャリーオーバーによる上乗せ分は、合計配当率45％とは別に加算されるということです。ロト7の場合、1等の当せん金は10億円になるまで上乗せされます。この場合、各等の配当率の合計はおよそ58％になり、ジャンボ宝くじの期待値（の価格に対する割合）を上回ります。
まとめ
期待値に注目すると、狙い目はジャンボ宝くじとキャリーオーバー時のロト6・ロト7ということになります。あくまで「1枚買ったときの期待値」に限った話ではありますが、参考にしてください。
これに限らず、自分の判断基準をしっかりと持って、暑い夏を乗り切りましょう。
