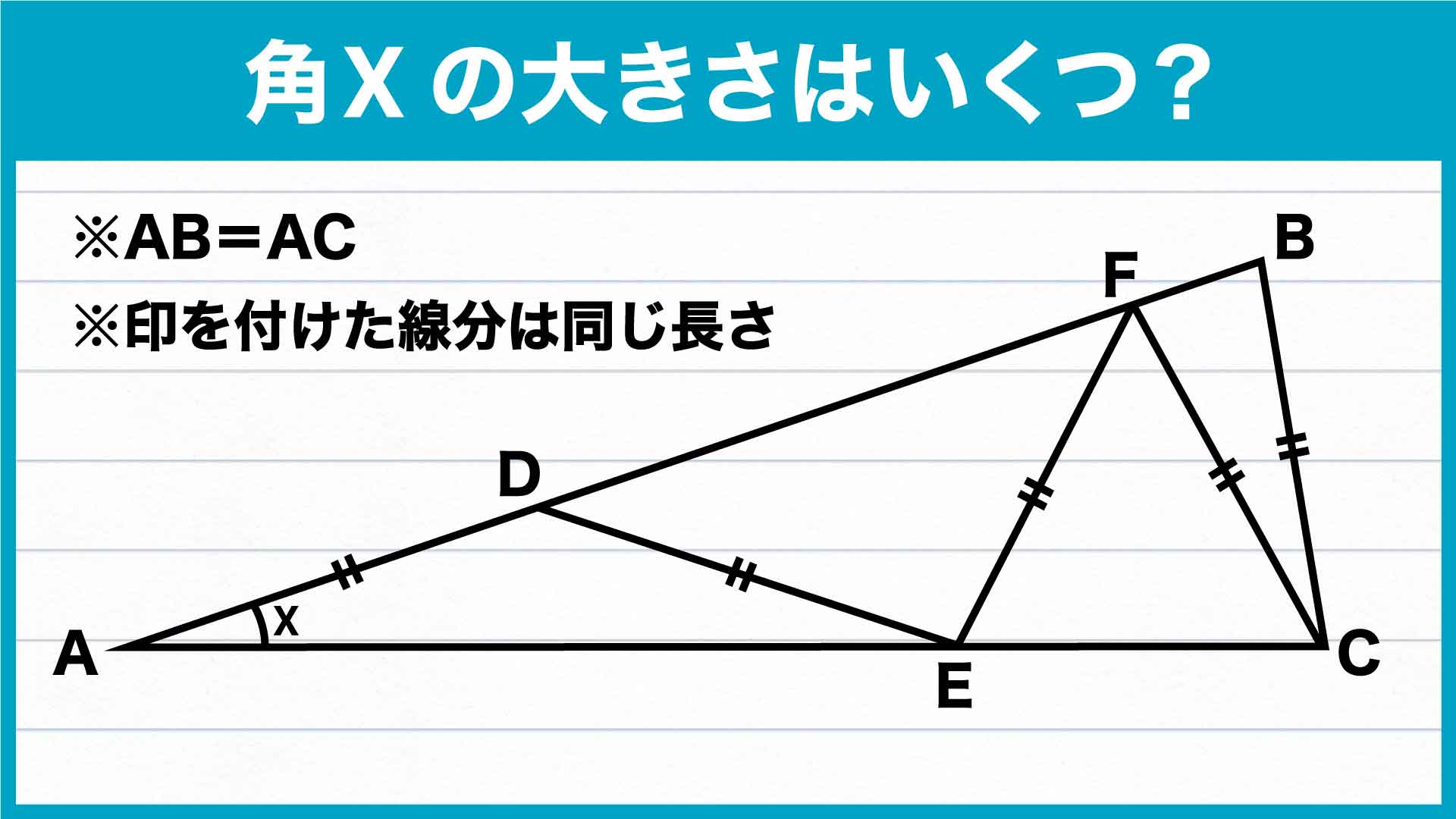
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
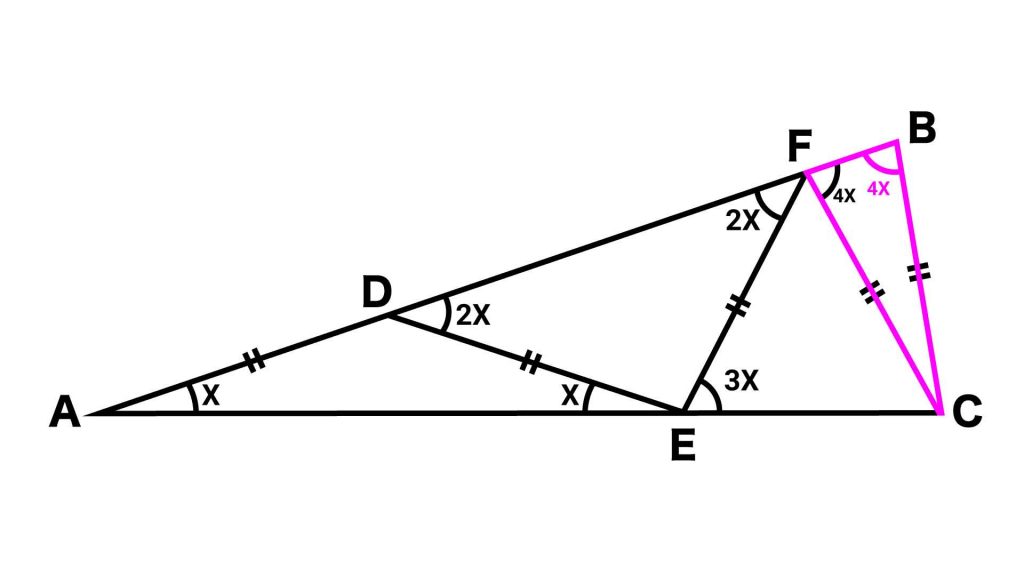
今回の解法のポイントは「三角形ABCの内角の和が、Xいくつ分かを求める」ことです。
与えられている角度は「X」しかありませんが、三角形の内角の和は180度であるため、三角形ABCのそれぞれの角度をXを使って表すことができれば、Xの値を求めることができます。
このために、Xで表すことができる角を順番に探していき、最終的に三角形ABCの残りの2角の角度を明らかにしていきます。実際には、三角形ABCはAB=ACの二等辺三角形なので、片方の角度がわかればゴールは近いです。
順番に角度を求めていく
ここから、「1つの三角形に着目し、それに関わる角度をXを使って表す」ということを繰り返していきます。
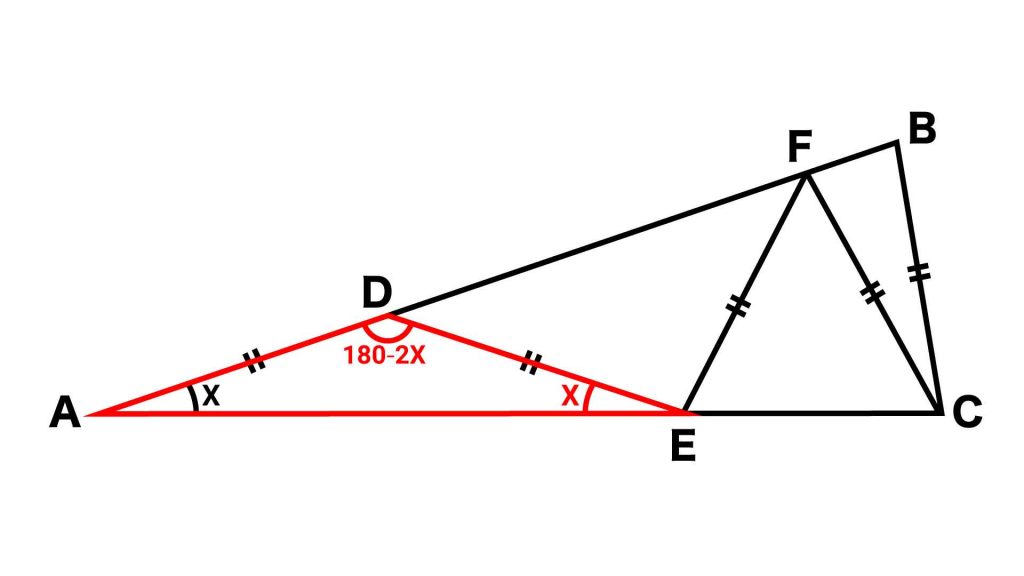
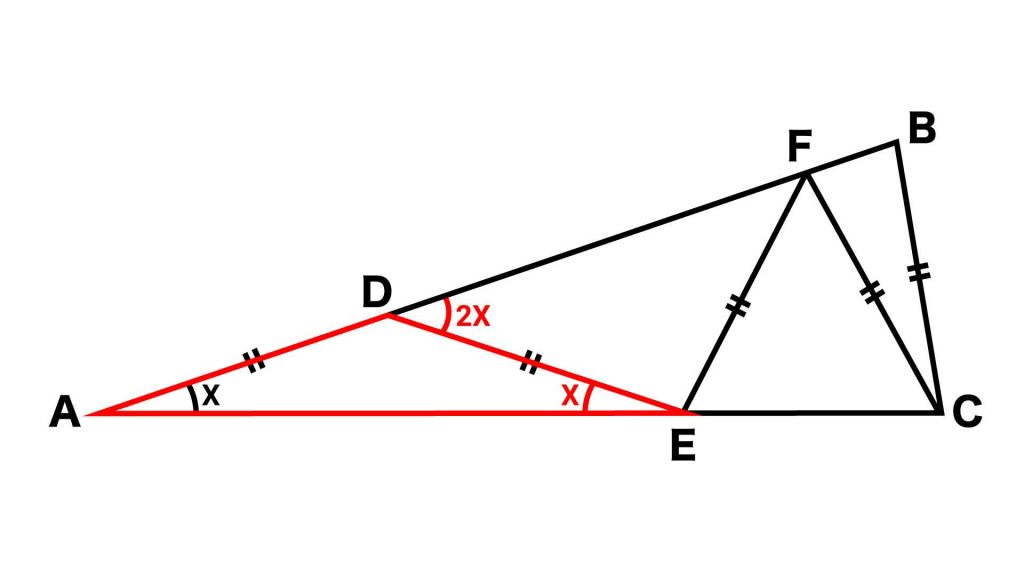
【ステップ1】三角形ADEに着目
まず、三角形ADEに着目します。
三角形ADEはDA=DEの二等辺三角形なので、角DEA=角DAE=Xです。三角形の内角の和は180度なので、残る角ADEの大きさは(180-2X)です。
一方で角FDEに着目すると、角FDEの角度は180度から角ADEを引いたものであることがわかります。このため、角FDEの大きさは、180-角ADE=180-(180-2X)=2Xです。
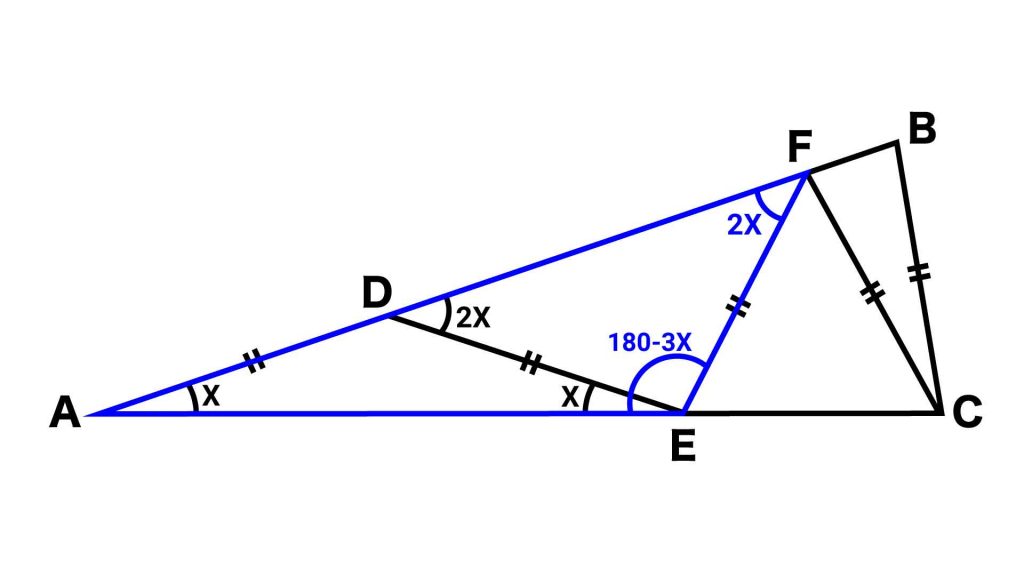
【ステップ2】三角形AFEに着目
次に、三角形AEFに着目します。
三角形EDFが二等辺三角形であることから、角AFEの大きさは2Xです。このため、角AEFの大きさは(180-3X)です。
したがって、三角形ADEのときと同じように計算すると、角FECの大きさは、180-角AEF=180-(180-3X)=3Xです。
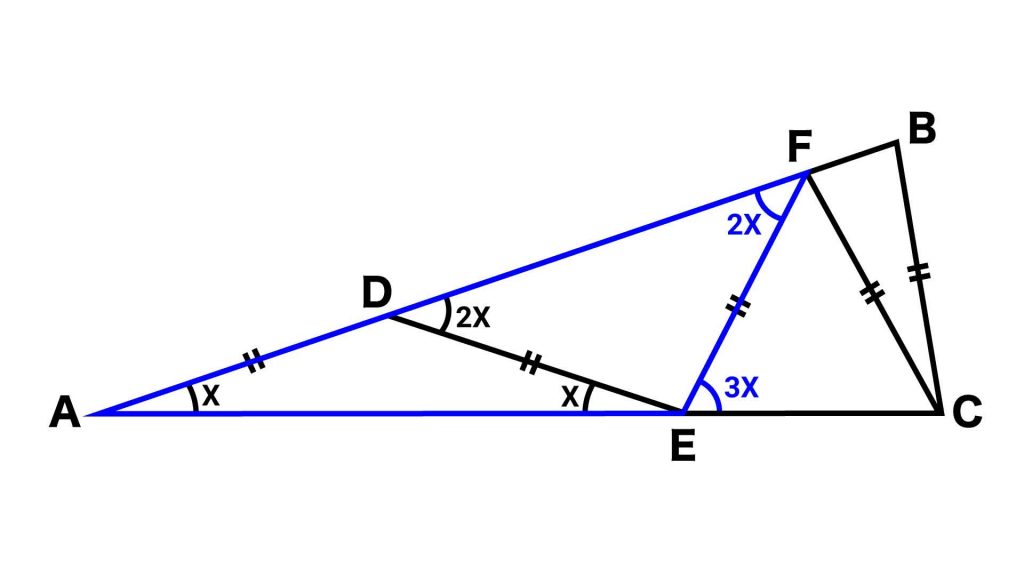
【ステップ3】三角形AFCに着目
次に、三角形AFC着目します。これまでのステップと同じように繰り返していきます。
三角形FECが二等辺三角形であることから、角FCEの大きさは3Xです。これより、角AFCの大きさは(180-4X)です。したがって、角CFBの大きさは、180-角AFC=4Xです。
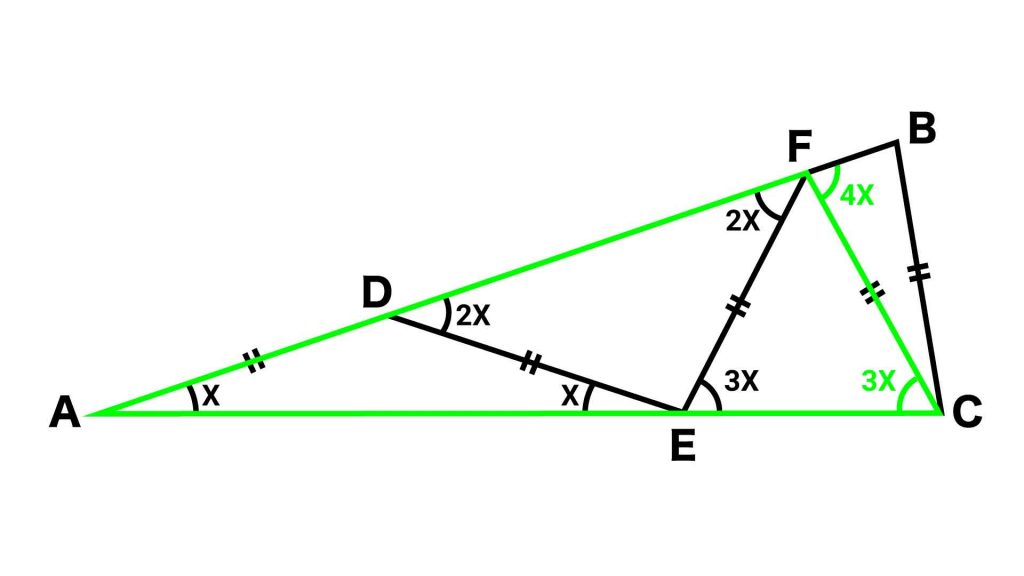
【ステップ4】三角形CFBに着目
次に、三角形CFBに着目します。
三角形CFBは二等辺三角形なので、角FBCの大きさは4Xです。
【ステップ5】ゴールはもうすぐそこ
最後に、三角形ABCに着目します。
三角形ABCは二等辺三角形なので、角ACBの大きさは4Xです。このため、角BAC=X、角ABC=角ACB=4Xとなり、三角形ABCの内角の和は、X+4X+4X=9Xと表されます。
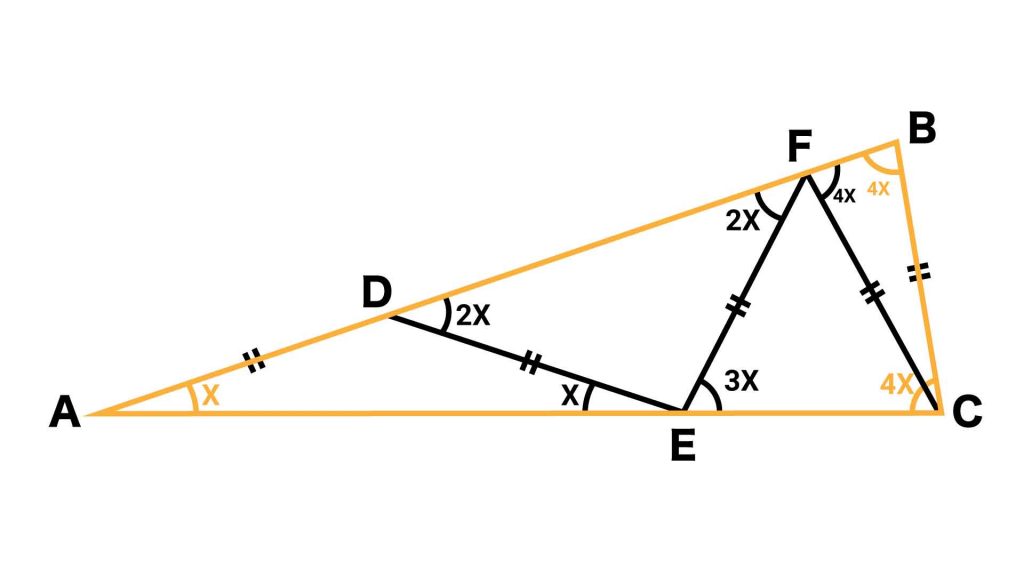
三角形の内角の和は180度なので、9X=180度。すなわち、X=20度となります。
答え:20度
地道に1つずつ角度を求められるかがポイントとなる問題でした。
それでは。
【あわせて読みたい】










.jpg)










.jpg)







