解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解法のポイントは「円の半径の長さは求めない」です。
円の面積は「(半径)×(半径)×(円周率π)」で得られるため、円の半径の長さを求めたくなりますね。ただし、この問題では半径の長さそのものがわからなくても、「(半径)×(半径)」の結果を求めることで答えを出すことができます。
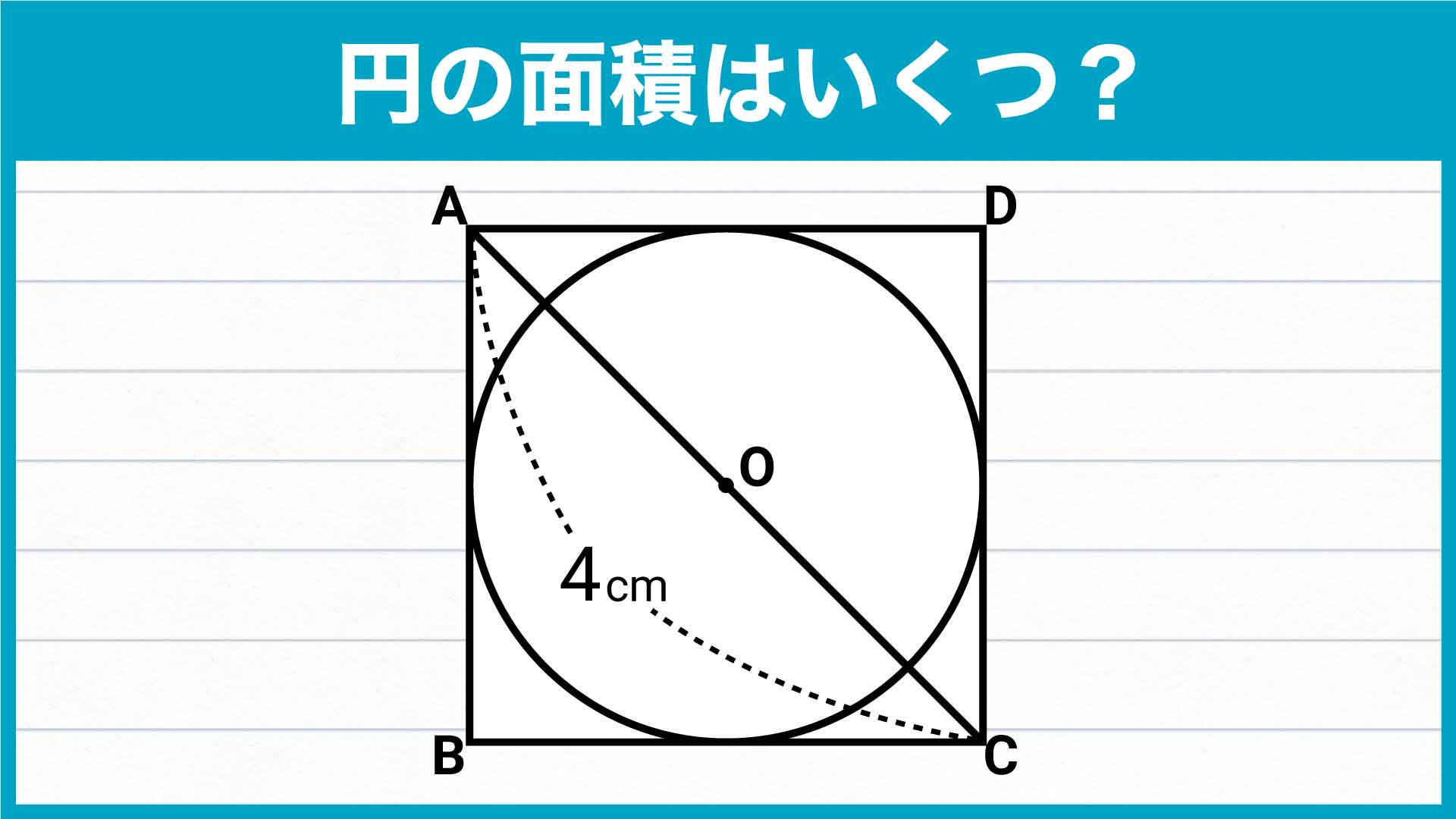
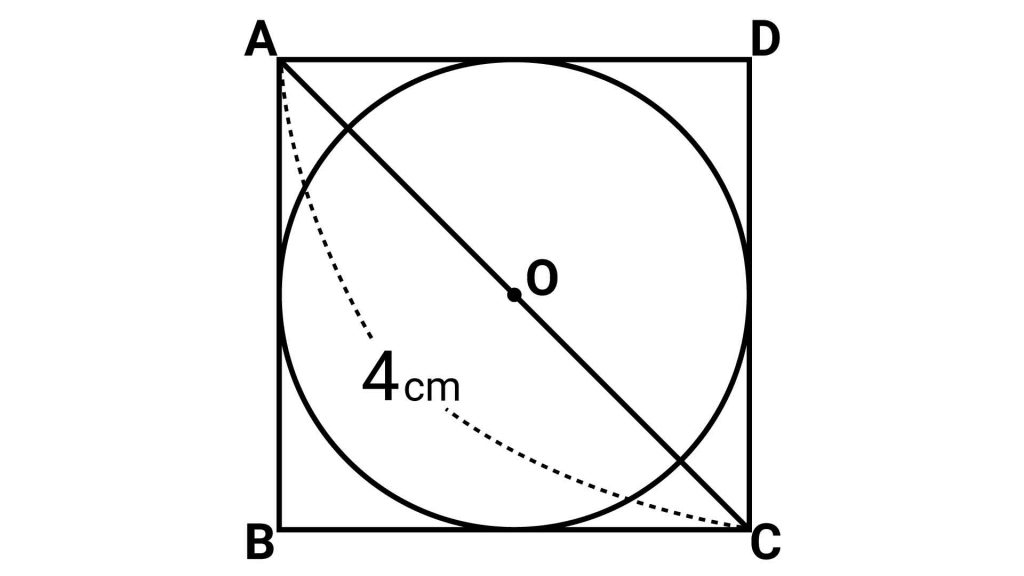
まず、正方形ABCDの面積を求めます。
対角線の長さが分かっている場合、正方形はひし形なので、ひし形の面積を求める公式「(対角線の長さ)×(対角線の長さ)÷2」から面積を求めることができます。
したがって正方形ABCDの面積は、4×4÷2=8cm2となります。
正方形を分割する
次に、正方形を分割します。
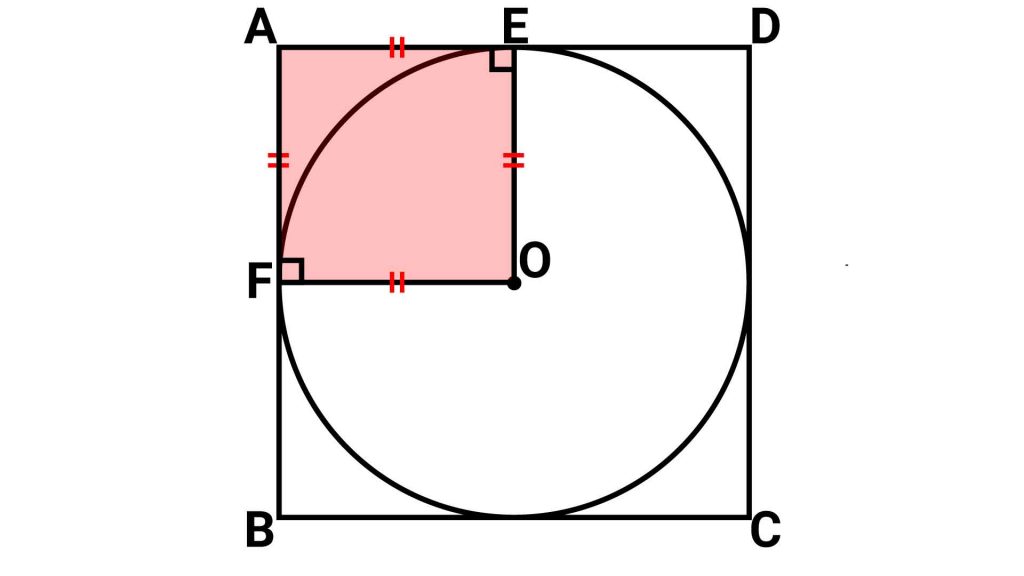
辺AD、辺ABと円の接点をそれぞれE、Fとし、点Oと結ぶと、四角形AFOEができます。
この四角形AFOEは、
- 線分OE、OFは同じ円の半径であるから、OE=OF。
- 点E、Fは辺AD、ABの中点で、AD、ABの長さは円の直径に等しいから、AE=FO、AF=EO。4辺の長さが等しいため、四角形AFOEはひし形。
- ひし形は向かい合う角が等しく、四角形の内角の和は360度であるから、四角形AFOEのすべての角は90度。
により、「すべての角が直角で、かつすべての辺の長さが等しい」ので、正方形となります。
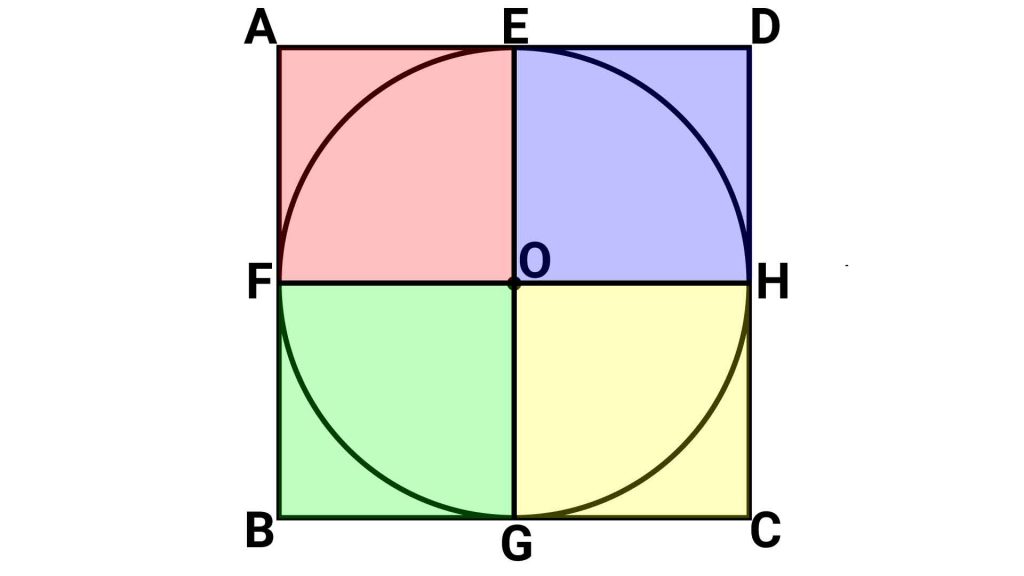
さらに、残り2つの接点をG、Hとすると、上と同じ考え方により、正方形ABCDは図のように赤、青、緑、黄の4つの小さな正方形に分けることができます。
これら4つの正方形の面積は等しいので、小さな正方形1つ分の面積は、正方形ABCDの面積の4分の1、すなわち、8÷4=2cm2となります。
これにより、OE×OF=2cm2であるとわかります。
円の面積は?
円の面積は、「(半径)×(半径)×(円周率π)」で求められます。
線分OEとOFは円の半径にに該当するため、「(半径)×(半径)」を求めるには、OE×OFを計算すればよいことになります。ここで、OE×OFは先ほど求めた小さな正方形1つ分の面積(2cm2)であることがわかっています。
したがって円の面積は、OE×OFに円周率をかけて、2π cm2となります。
答え:2π cm2
半径そのものを求めなくても、「(半径)×(半径)」の結果を求めることで解きやすくなる問題でした。
正面突破できなくても、視点を変えれば突破口なんてたくさんあるものです。
それでは。
【あわせて読みたい】










.jpg)









.jpg)







