解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
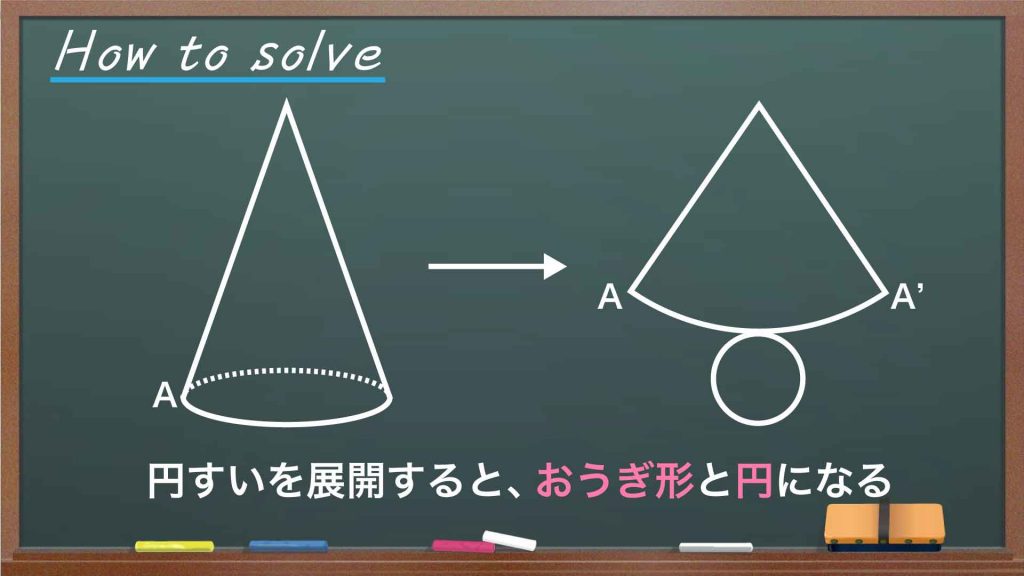
今回のポイントは、「展開図を使う」ことです。
円すいの展開図は、おうぎ形と円から構成されます。
一見イメージするのが難しい立体図形の問題も、展開して平面図形にしてしまえば、ずいぶんと解きやすくなります。
以上を踏まえ、問題を解いていきましょう!
円すいを展開する
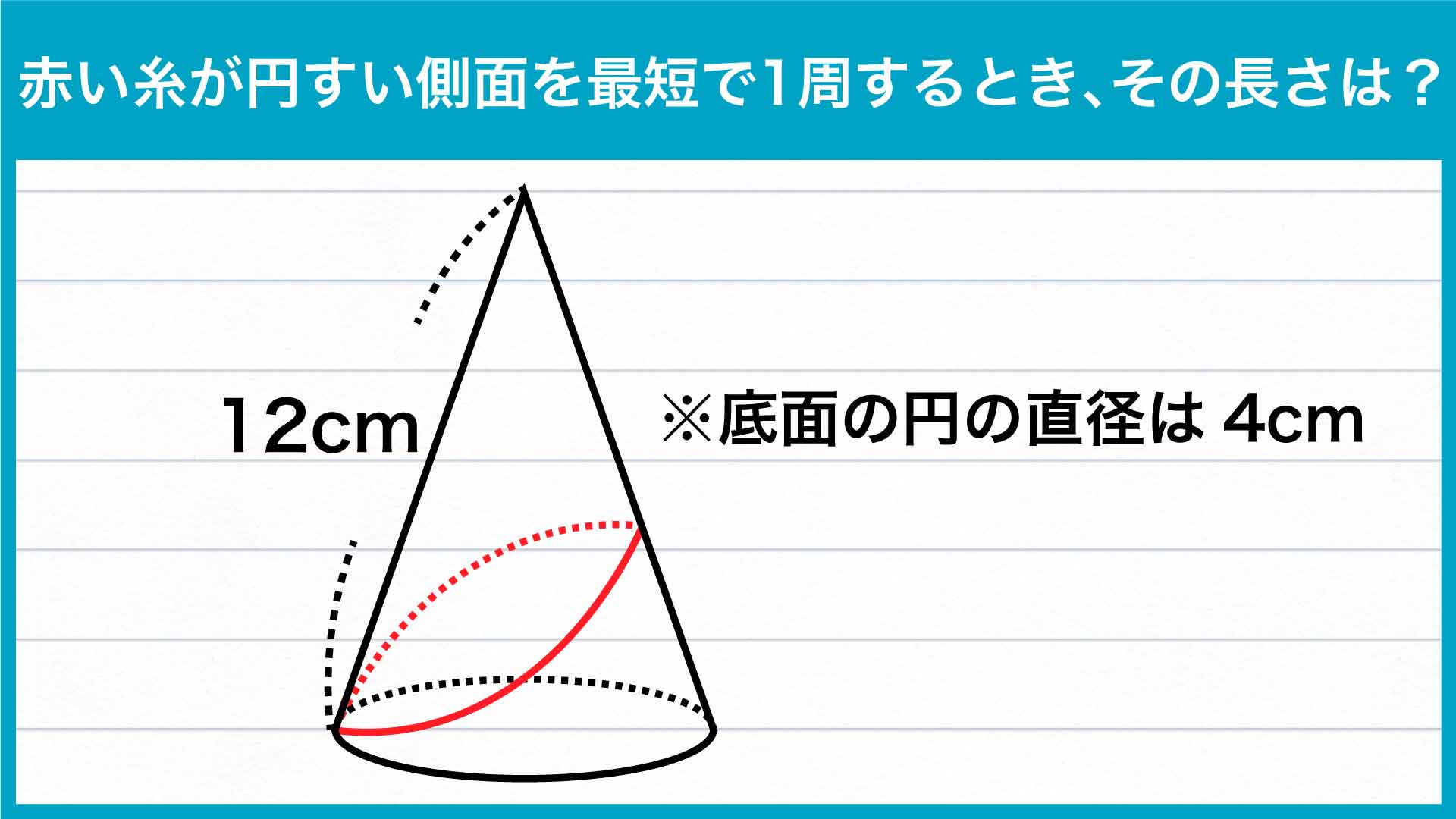
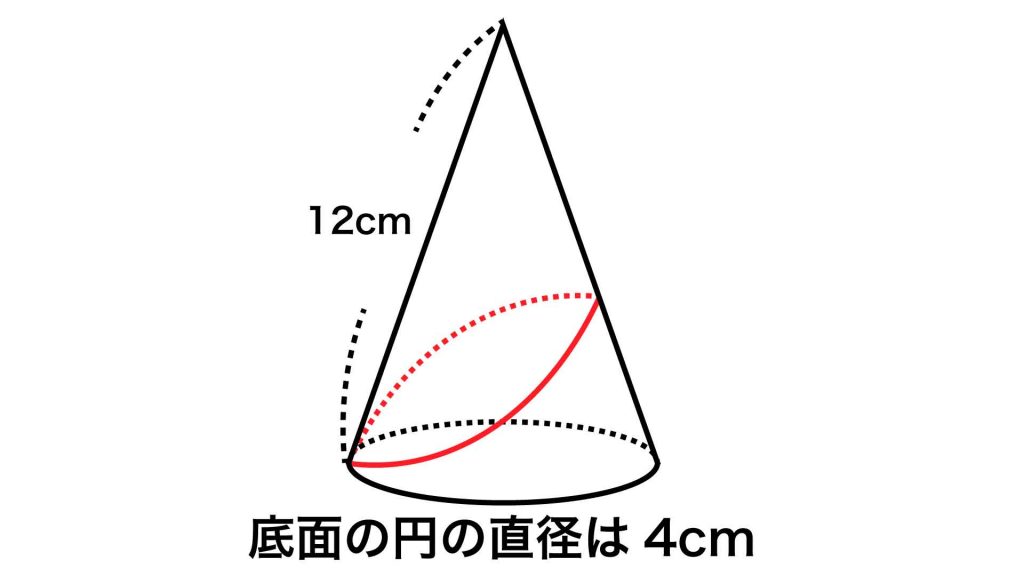
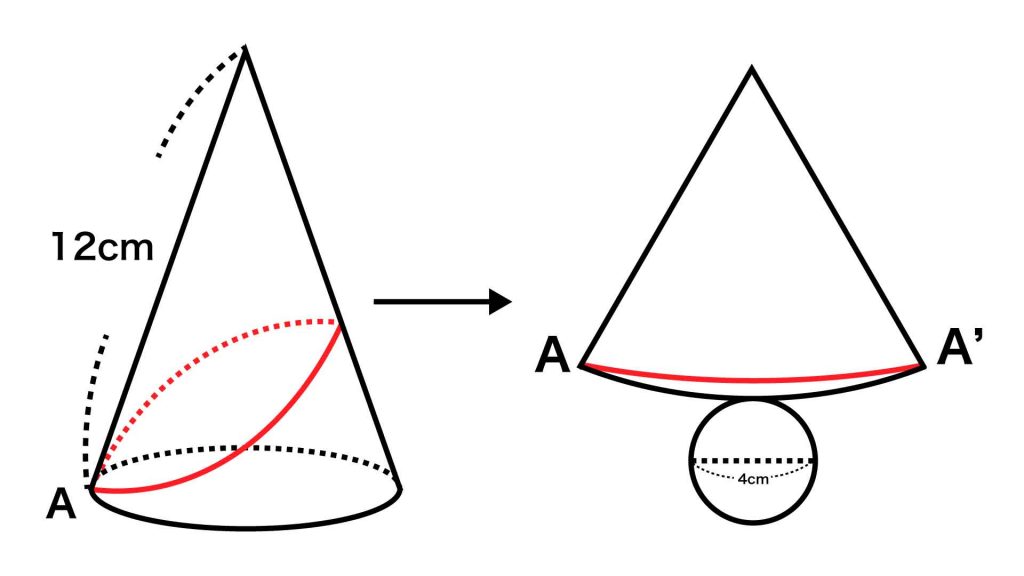
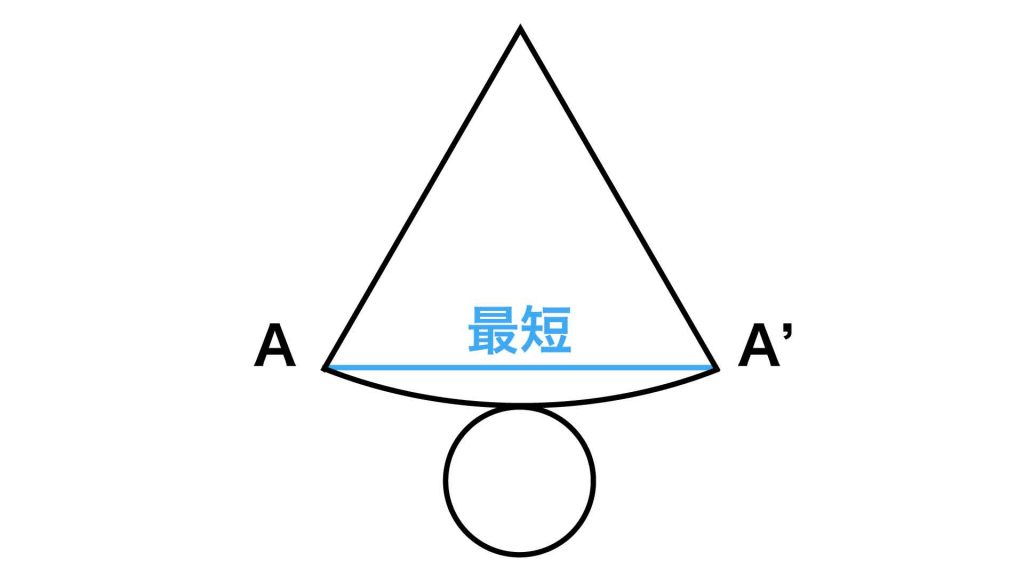
まず、糸が巻かれた円すいを展開します。
すると、糸のかけ始めの点である点Aと、かけ終わりの点である点A'(もとの立体図ではAと重なっている)のあいだに、糸である赤線が引かれているのがわかります。
そして、この赤線がもっとも短くなるのは、点Aと点A'を一直線に結んでいるときです。
おうぎ形の中心角を求める
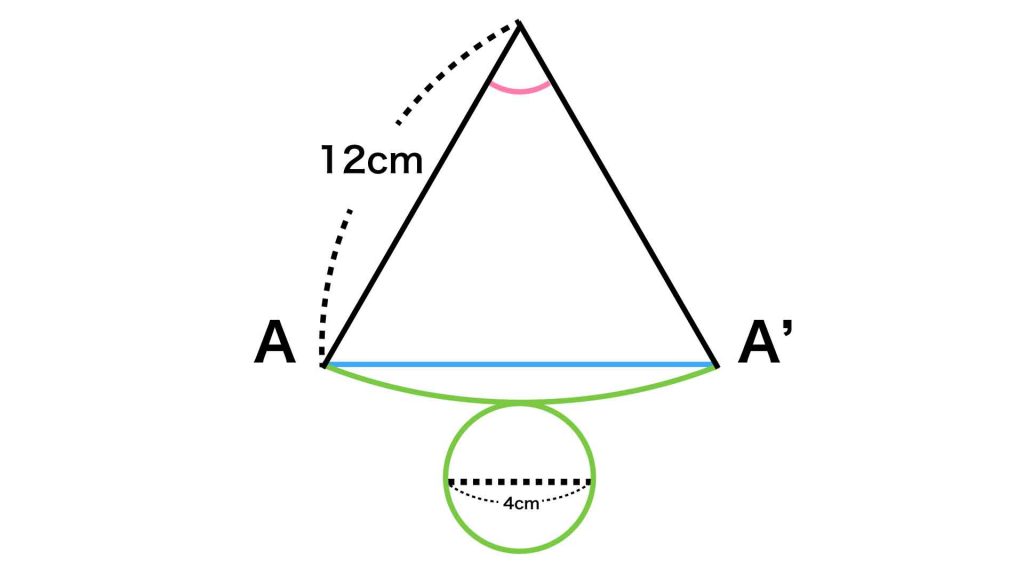
糸の長さを導きだすためには、まだ情報が足りません。この問題を解くうえで必要となる情報は、おうぎ形の中心角の大きさです。したがって、ここでは中心角の大きさを求めていきます。
円すいの展開図における、円とおうぎ形の弧の部分は、もとの立体図形では重なっていました。つまり、円の周りの長さとおうぎ形の弧の長さは等しいのです。
円の周りの長さは、4×π=4πcmとなります。
おうぎ形の弧の長さも同じく4πcmなので、おうぎ形の中心角を〇度とすると、
12×2×〇/360×π=4πcm
という式が成り立ちます。この式を計算すると、〇に入る値は60となります。したがって、おうぎ形の中心角は60度です。
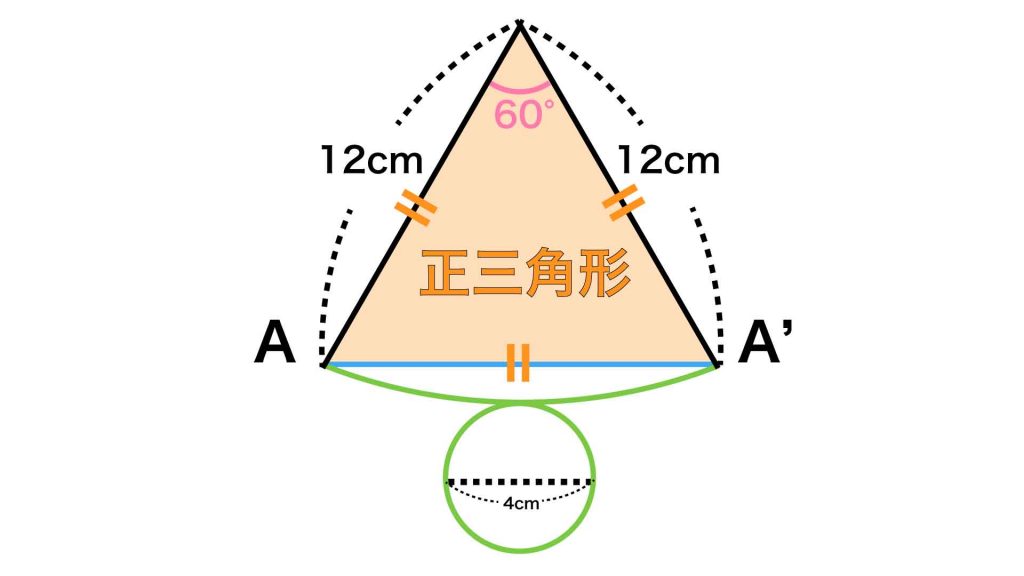
すると、おうぎ形の2本の半径と糸の線によってつくられる三角形は、一辺が12cmの正三角形だということがわかります。
よって、糸の線の長さは、おうぎ形の半径と同じ12cmと求まります。
答え:12cm
またの挑戦をお待ちしています!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)






