解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回のキーワードは「補助線」です。
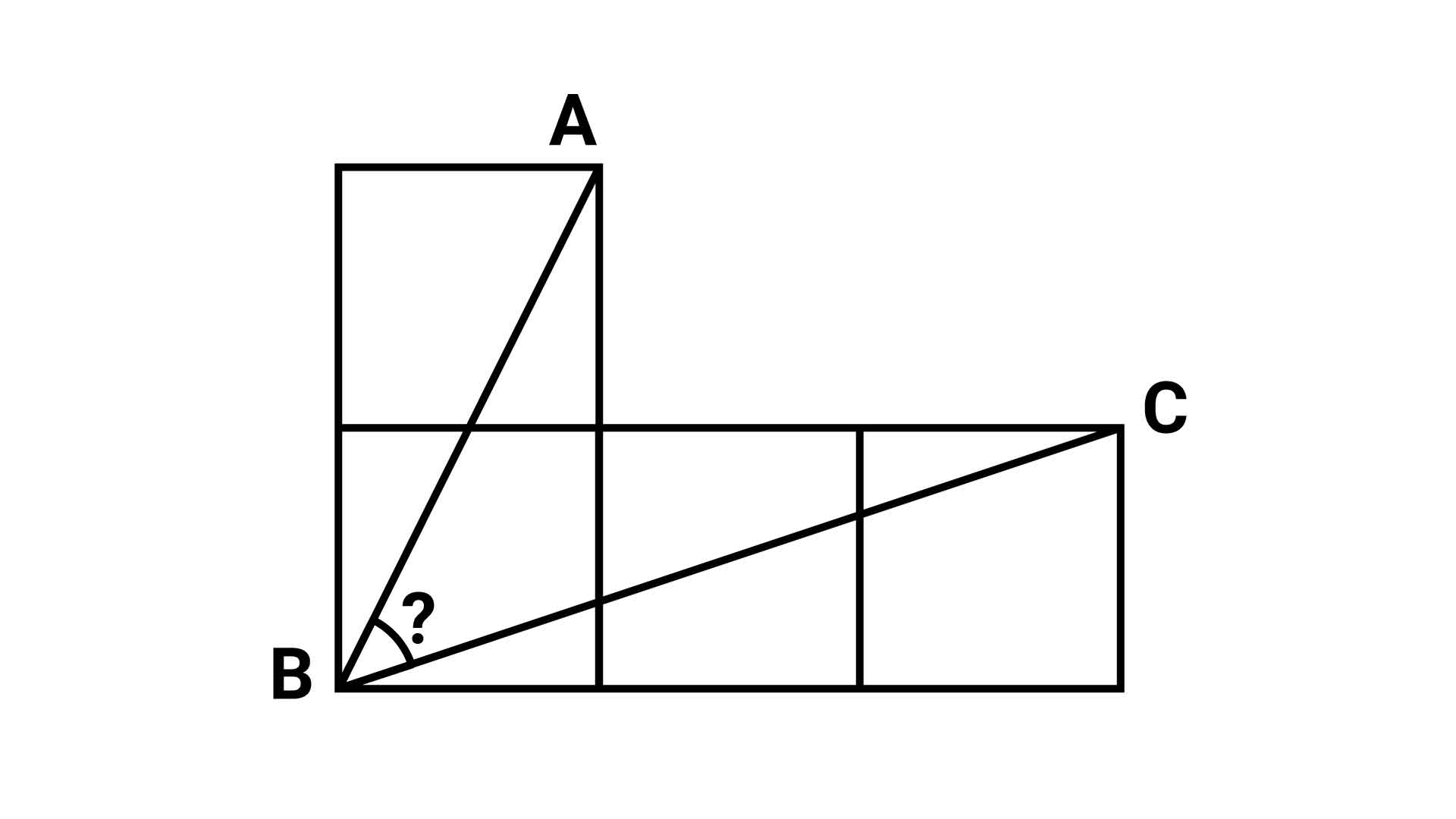
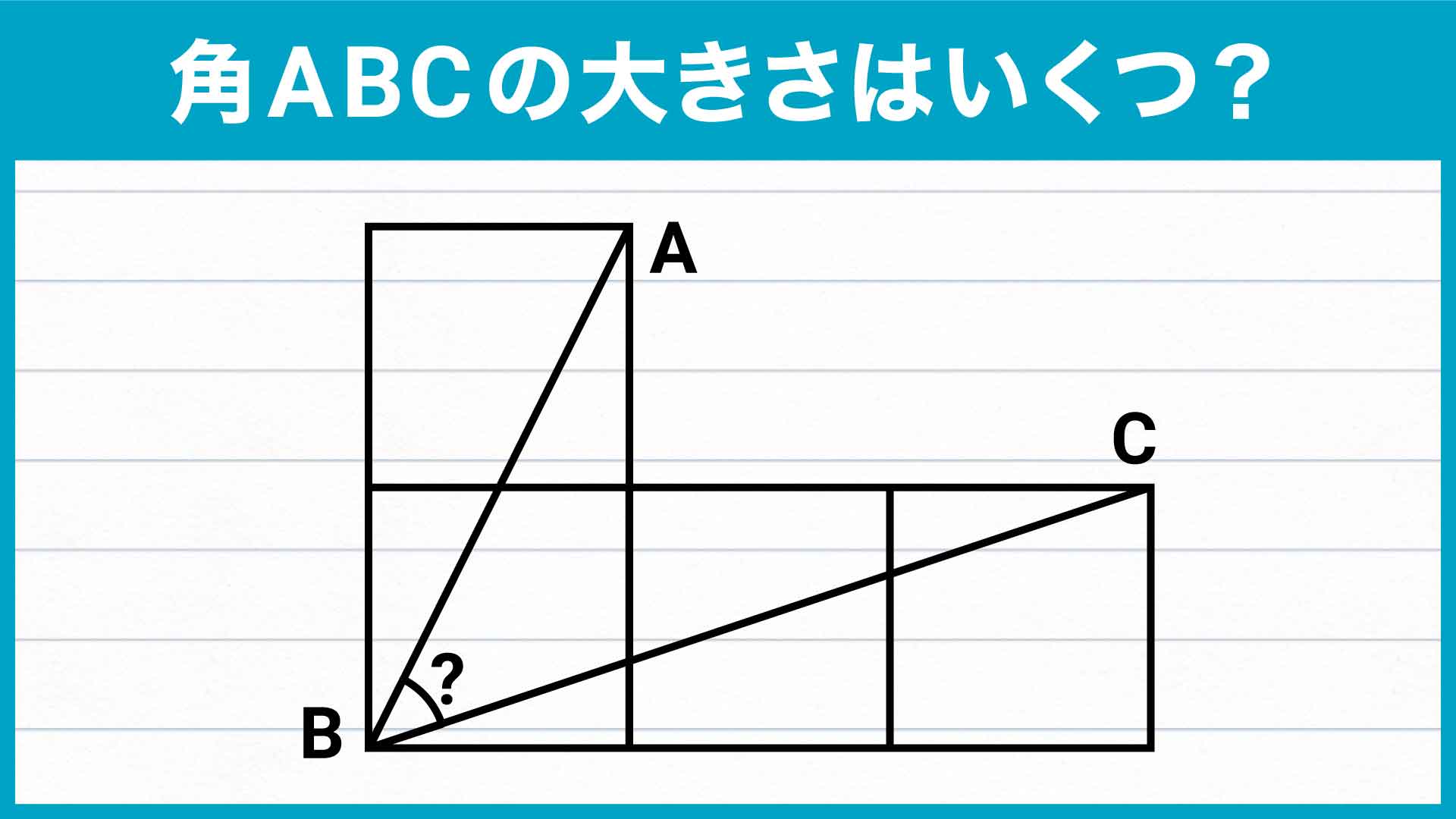
問題を解くカギとなる補助線は、頂点AとCを結ぶ直線です。
これにより、三角形ABCができ、求める角度はその内角の1つとなります。
ここではよりわかりやすく、正方形を2つ書き足した図を使用します。
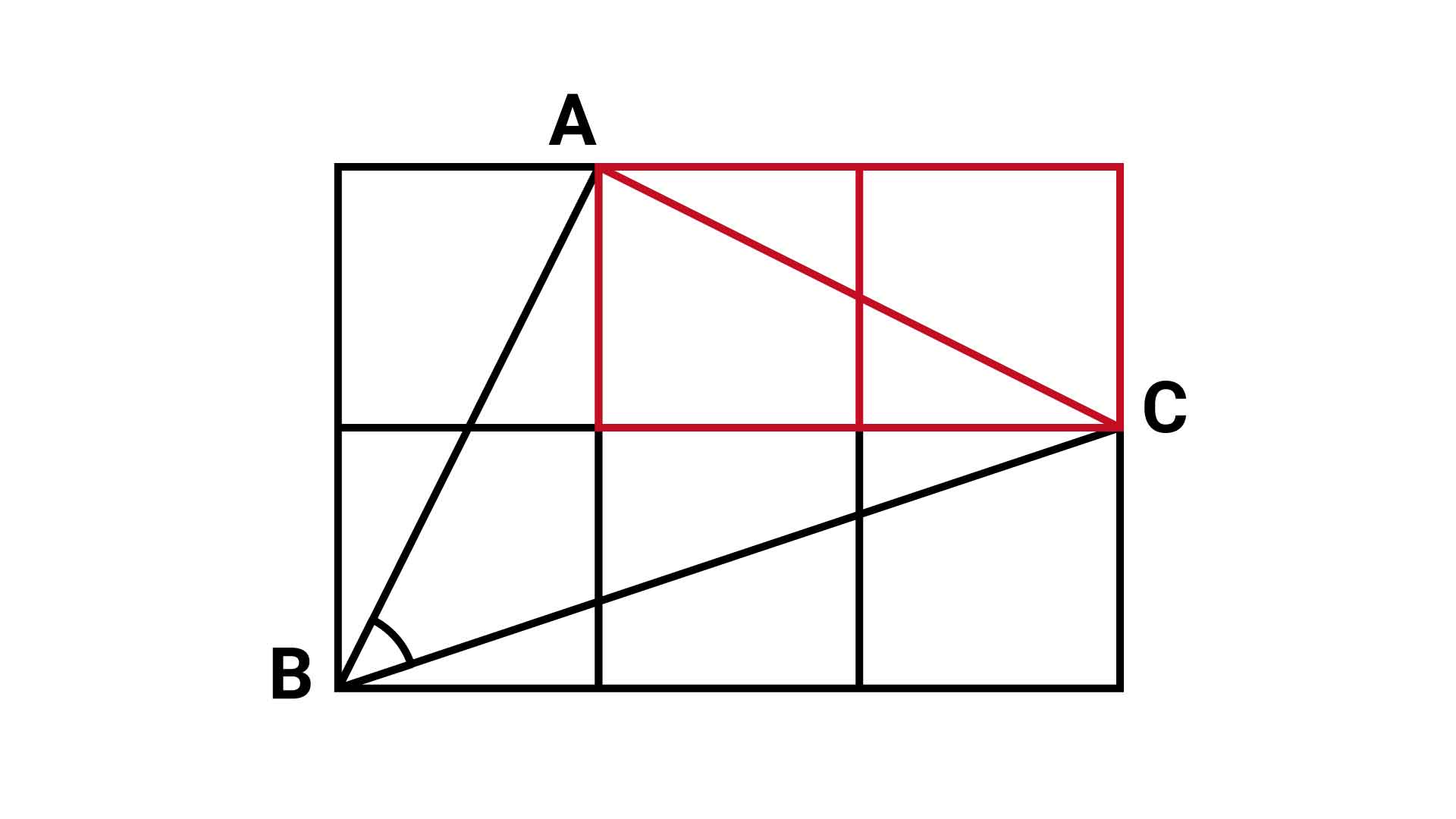
三角形ABCに注目!
できた三角形ABCについて考えます。まずは辺に着目しましょう。
辺ABと辺ACは、ともに正方形を2個並べてできる長方形の対角線ですから、同じ長さになります。
このため、AB=ACとなり、三角形ABCは二等辺三角形であることがわかります。
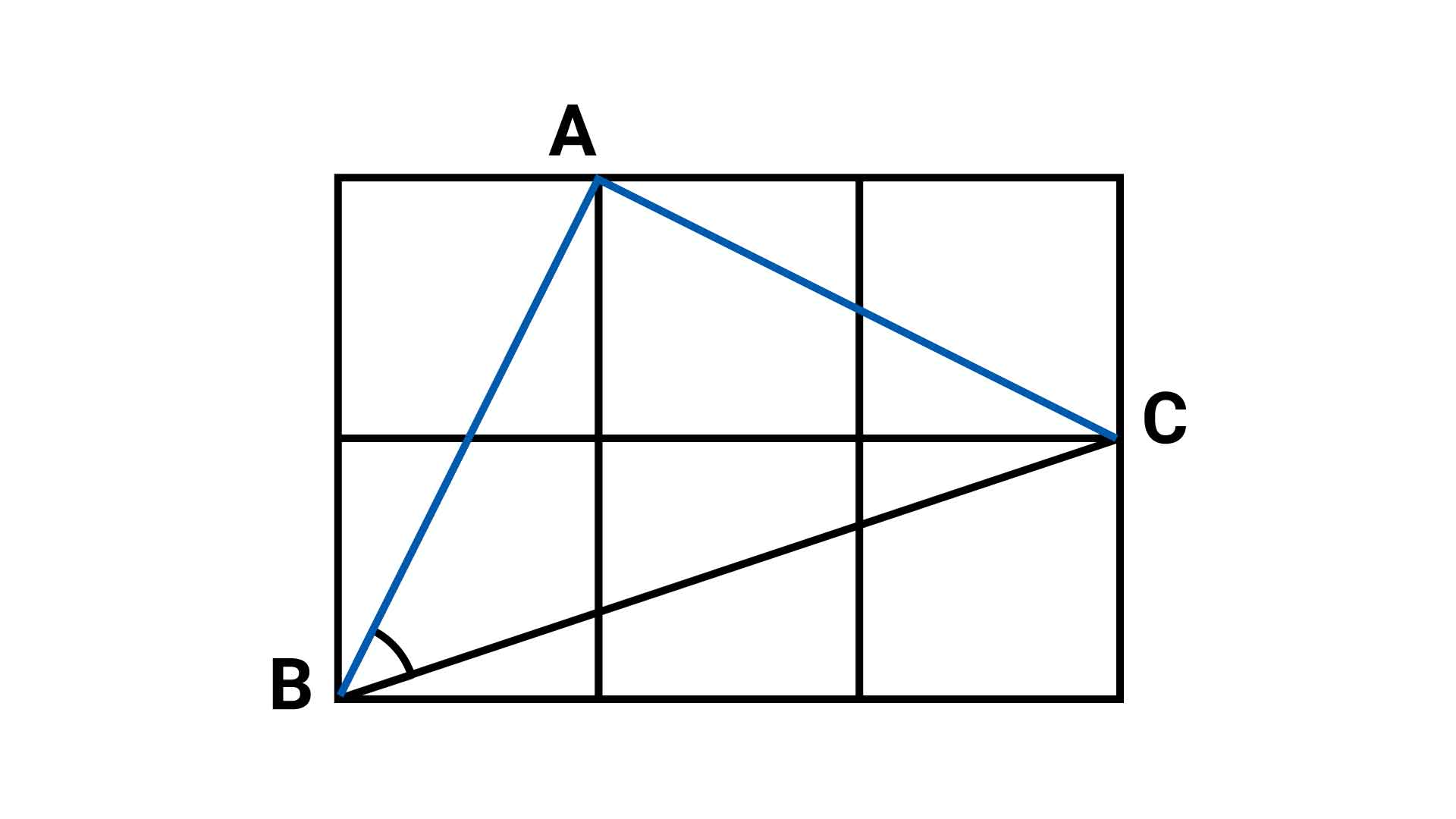
次に、角BACに注目します。
角BACは下の図のように、正方形を2つ並べてできる直角三角形の内角(〇、×)の和であることがわかります。
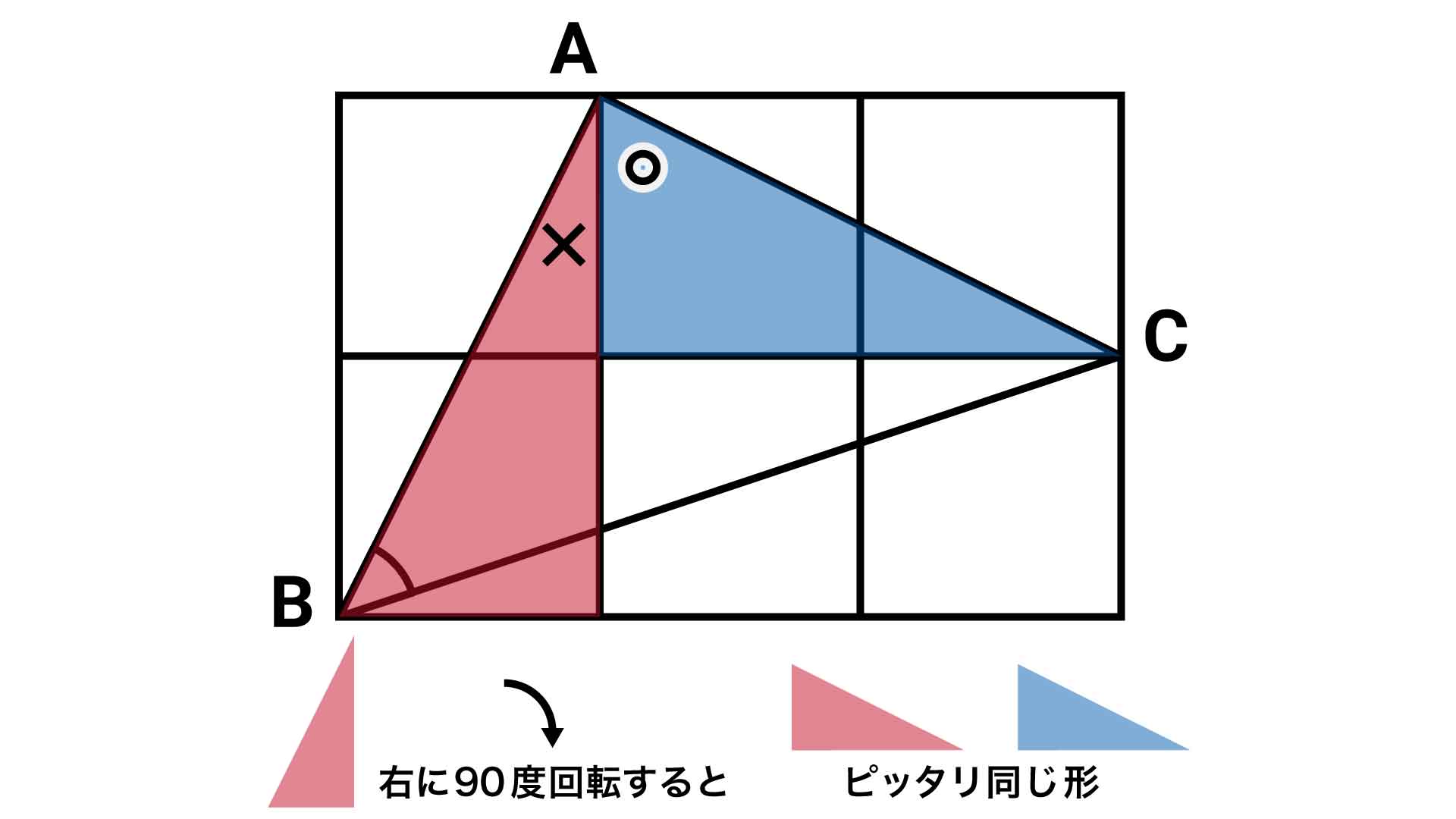
ここで、上の図の赤い直角三角形を右に90度回転させると、青い直角三角形とピッタリ重なります。
なので、この2つの直角三角形は全く同じ形です(これを合同といいます)。
ピッタリ重ねられるということは、下の図中の〇、×の角度はそれぞれ同じになります。
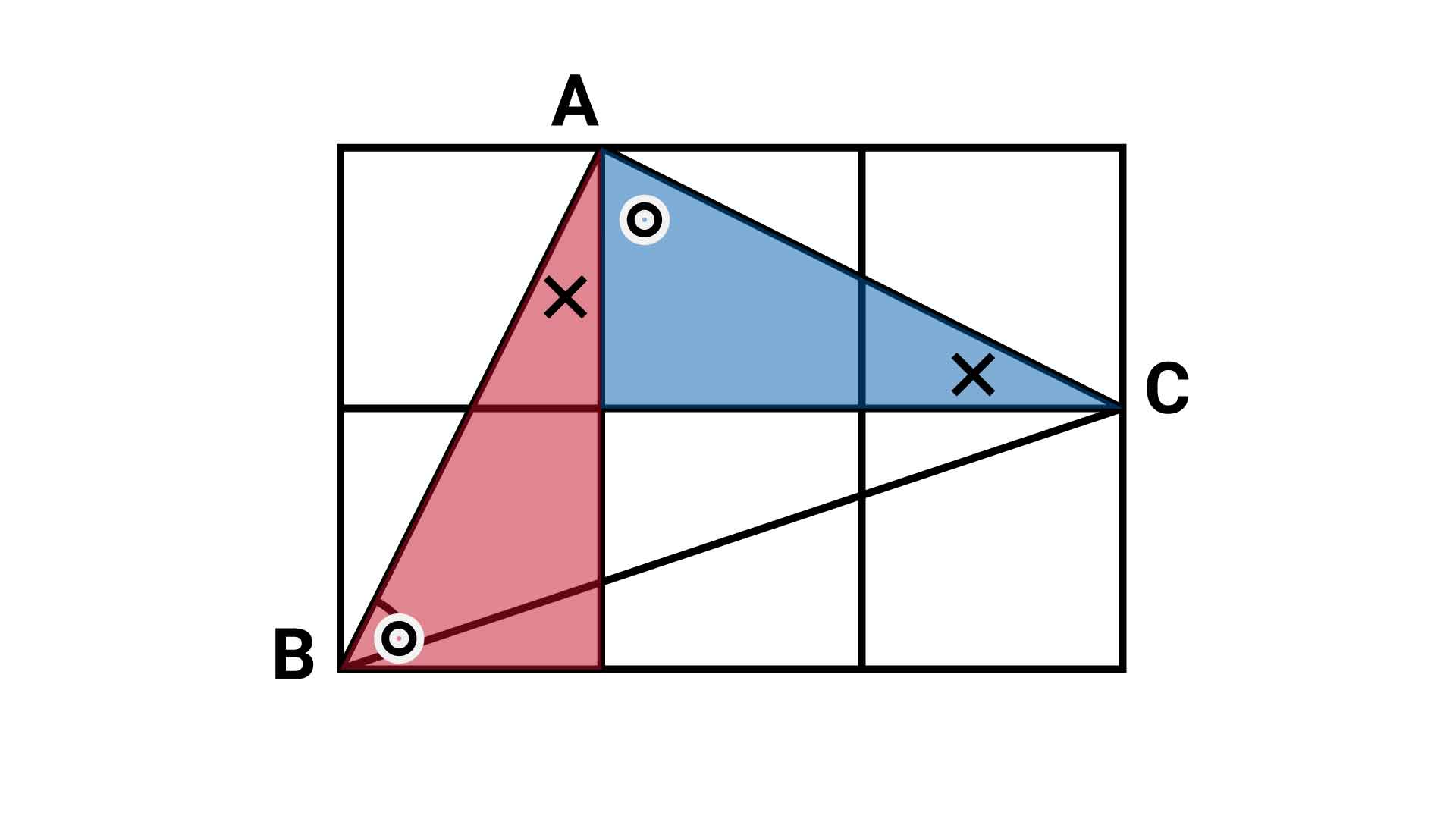
いずれか一方の三角形に着目すると、三角形の内角の和は180度、加えて直角三角形は1つの角が直角(90度)であるため、それぞれの角度がわからなくとも、〇の角度と×の角度を足すと90度になることがわかります。
角BACは赤い直角三角形の×の角と、青い直角三角形の〇の角で成り立っているので、角BACの大きさは90度です。
三角形ABCは〇〇だった!
以上から、三角形ABCは、
- AB=AC
- 角BACの大きさが90度
なので、直角二等辺三角形です。
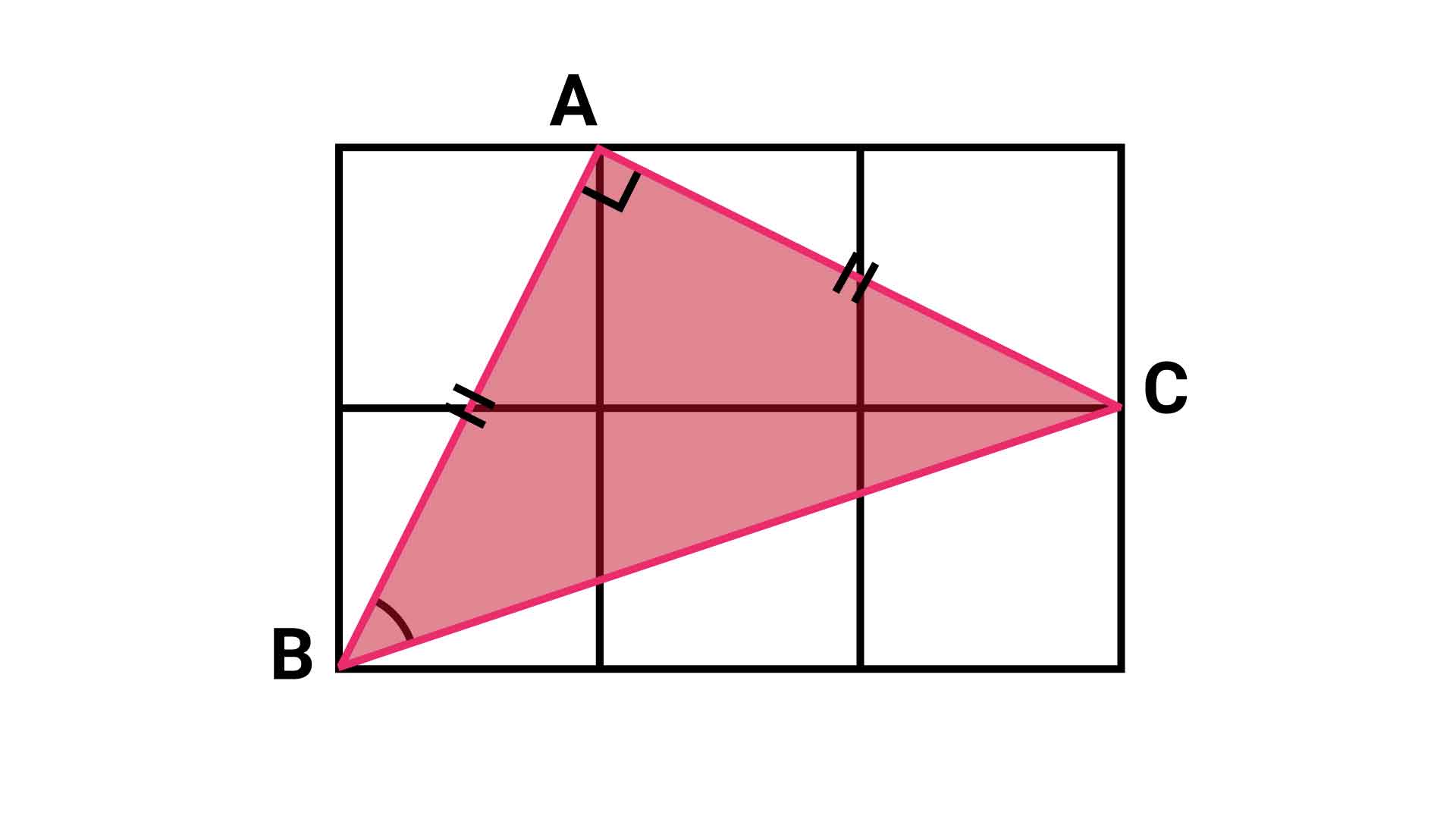
求める角度は直角でない角度の1つなので、(180-90)÷2=45度となります。
答え:45度
とっかかりをつかめないときは、図にいろいろ書いてみましょう。とにかく手を動かせば、何かが見えてきます。
それでは。
【あわせて読みたい】














-1-1024x683-1.jpg)













