解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
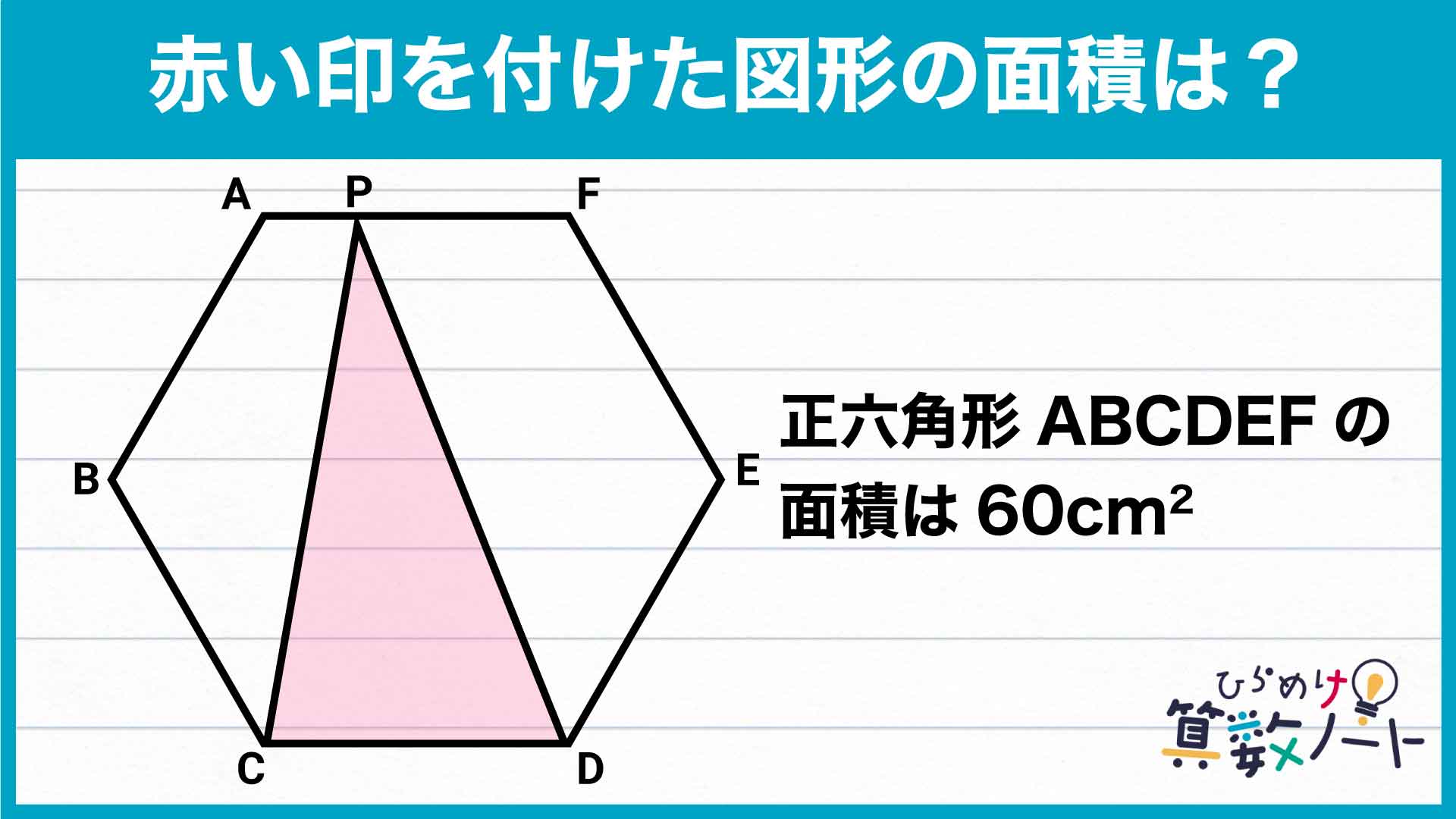
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
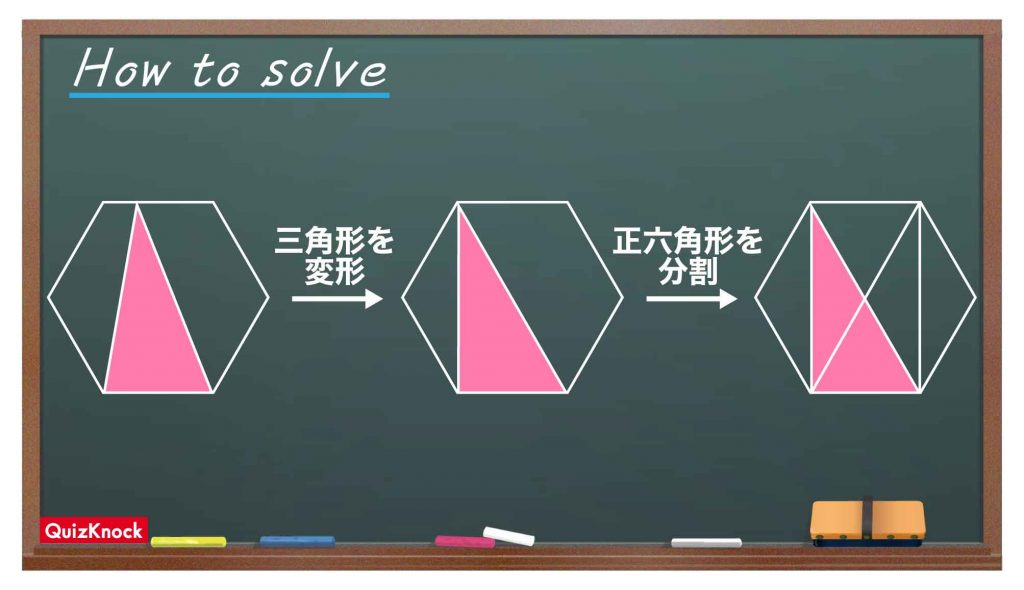
今回の問題の解き方をまとめた図がこちらになります。ポイントは次の2点です。
- 三角形を変形する
- 正六角形を6つの三角形に分割する
この図の流れに沿うことで、面積を求めたい三角形と同じ面積を持つ図形が見えてきます。
この図の流れに沿って、順に解いていきましょう!
まずは三角形の面積を変えずに変形
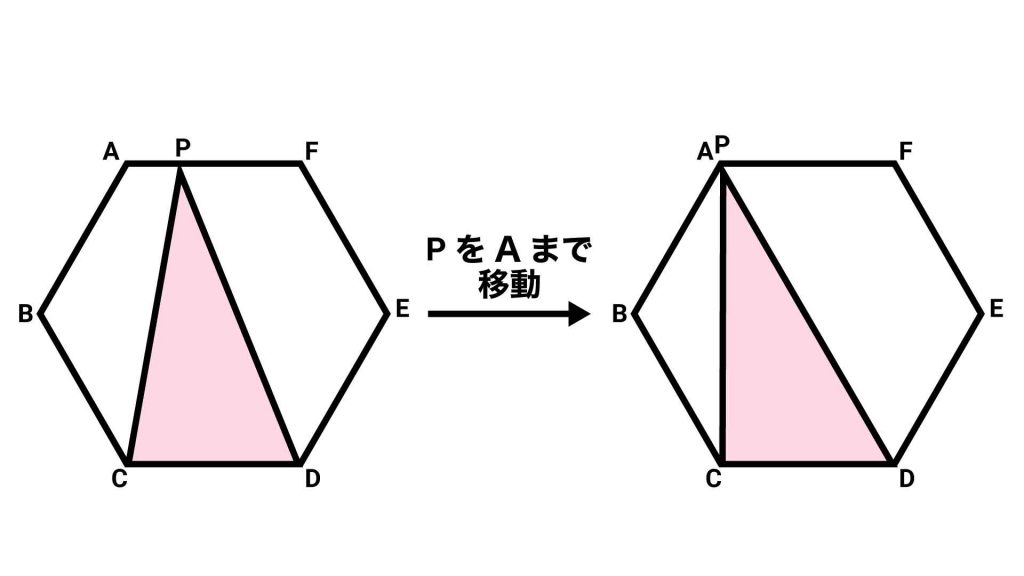
下の図をご覧ください。
正六角形の向かい合う辺は互いに平行です。辺CDを三角形PCDの底辺とすると、頂点をPからAへと移動させても、三角形の高さは変わらないため面積も変わりません。
したがって、上の図の三角形PCDと三角形ACDの面積は等しくなります。ここからは、三角形ACDの面積を求めていきます。
正六角形を6つの三角形に分割
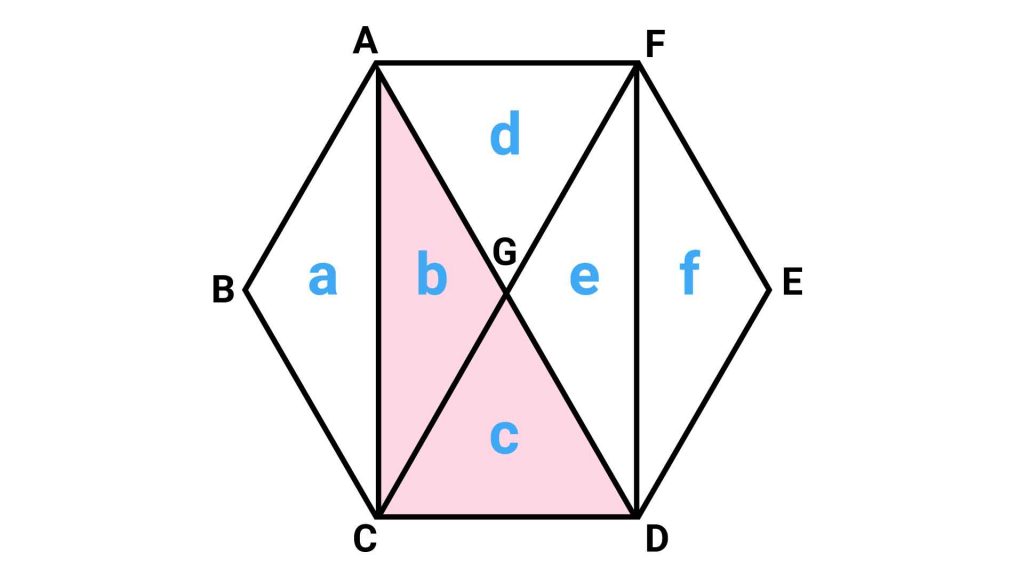
次に、以下の図のように正六角形を分割します。
a~fの6つの三角形に分割できました。三角形ACDは、三角形bとcを合わせた図形となります。
三角形bとcの面積と正六角形の関係は?
三角形a~fの面積について考えていきましょう。
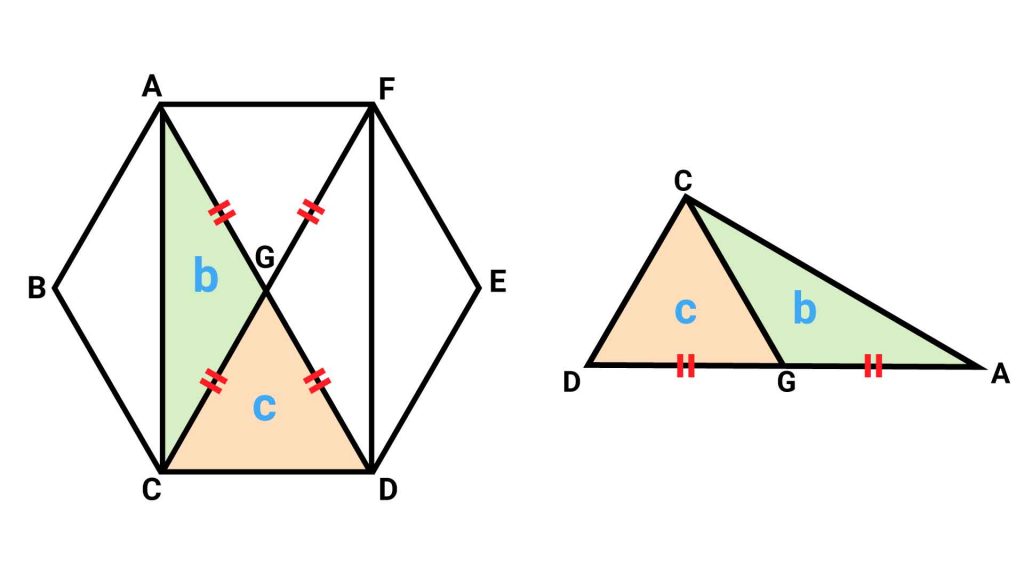
まず、三角形bとcに注目します。
四角形ACDFは長方形であり、対角線ADとFCはそれぞれの中点で交わります。したがって、AGとGDの長さは等しくなります。
三角形bの底辺をAG、三角形cの底辺をGDと見ると、三角形の高さが等しくなっています。したがって、三角形bとcの面積は等しくなります。
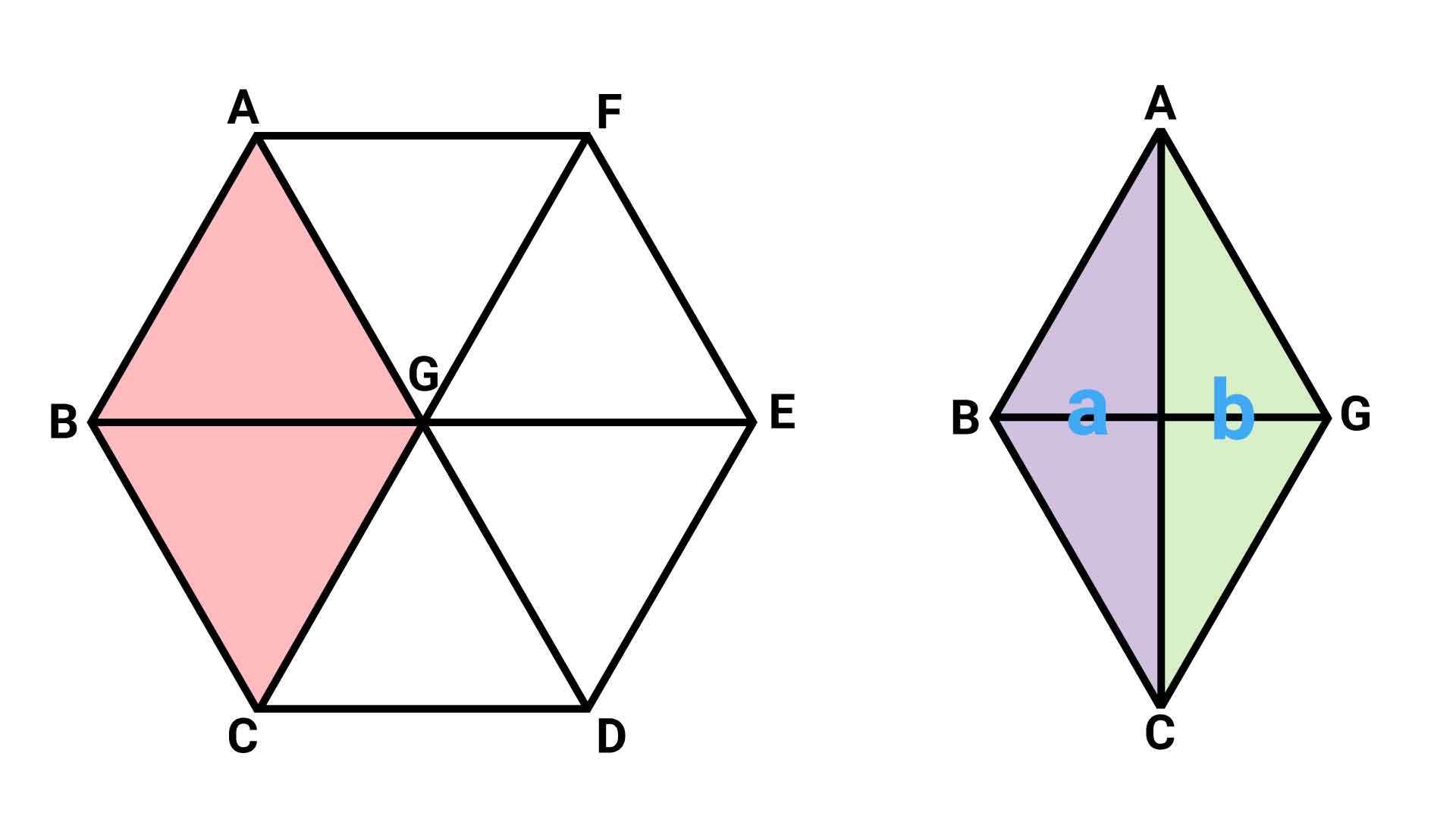
次に、三角形aとbの面積を比較します。そのために、正六角形を別の形で分割してみます。
上の左の図のように、正六角形は、正三角形を6つ組み合わせた図形です。
また、右の図のように、三角形aとbはそれぞれ、2つの正三角形を組み合わせた図形を、縦に2分割した図形となります。
上下それぞれの正三角形は直線BGを軸として線対称です。したがって、三角形aとbは直線ACに関しても線対称であり、直線ACで折るとぴったり重なるため、三角形aとbの面積は等しくなります。
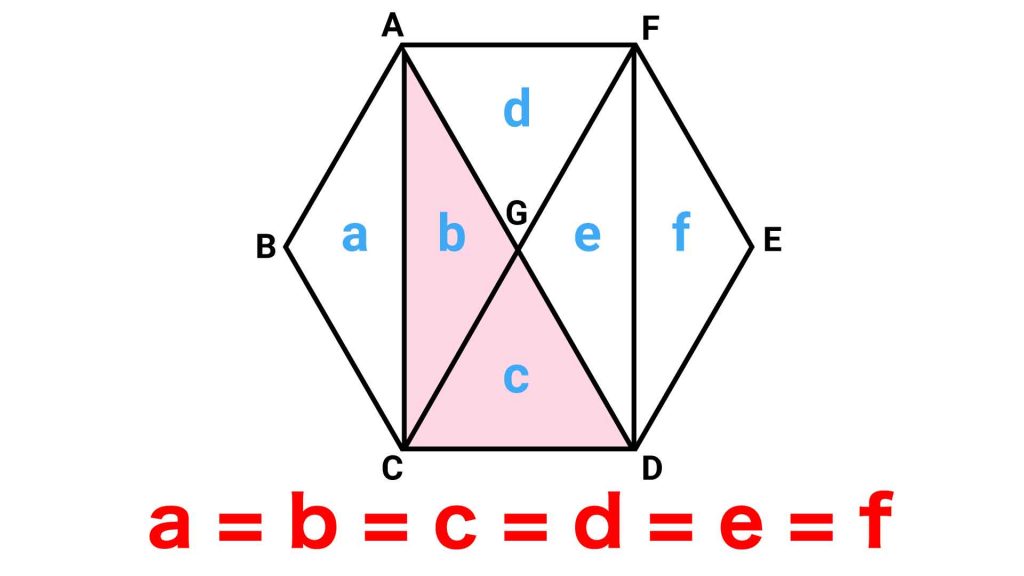
上と同様の考え方で三角形d、e、fを見ると、直線ADで正六角形が2等分されていることから、三角形a~fの面積が全て等しいことが示せます。
三角形ACDの面積を求める
三角形a~fは、正六角形の面積を6等分しているので、それぞれの三角形の面積は60÷6=10cm2です。
三角形ACDは、三角形bとcを合わせた図形で、面積は10×2=20cm2となります。
求めたい三角形PCDの面積は三角形ACDの面積と等しいので、20cm2です。
答え:20cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







