解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
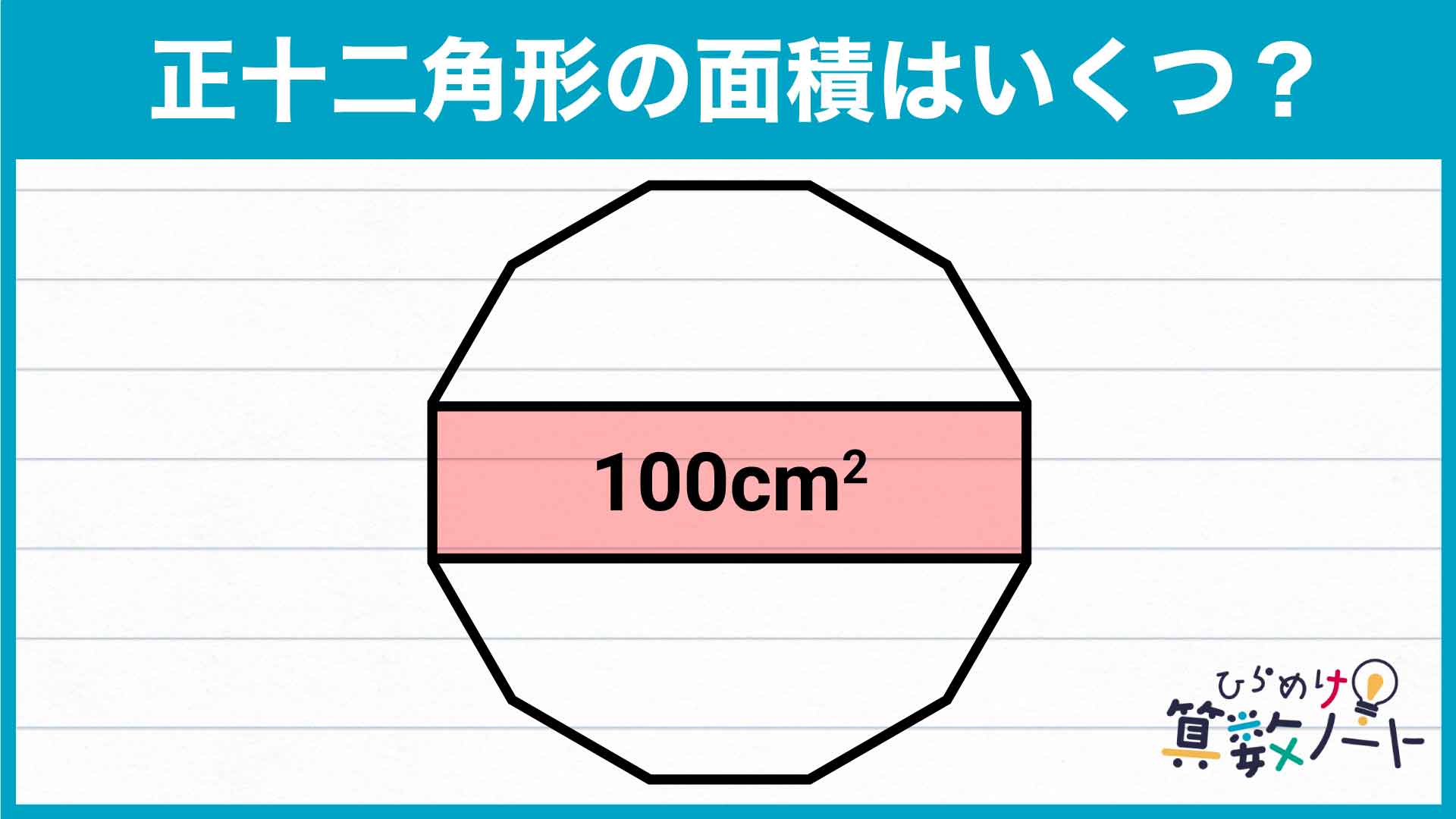
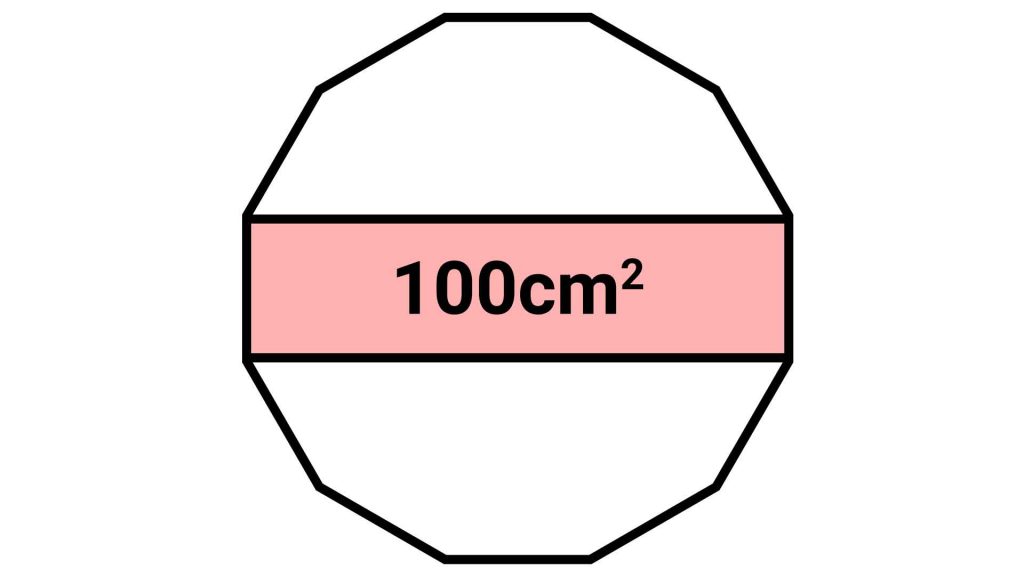
今回も僕と一緒に解いていきましょう！ 現時点で明かされている情報は「長方形の面積が100cm2であること」だけ。ここからどうすれば解けるのでしょうか？
今回の問題を解くうえで重要なポイントは、「正十二角形を分割すること」です。こうすることで、突破口が見えてきます。
どのように分割するか、以下の図をご覧ください。
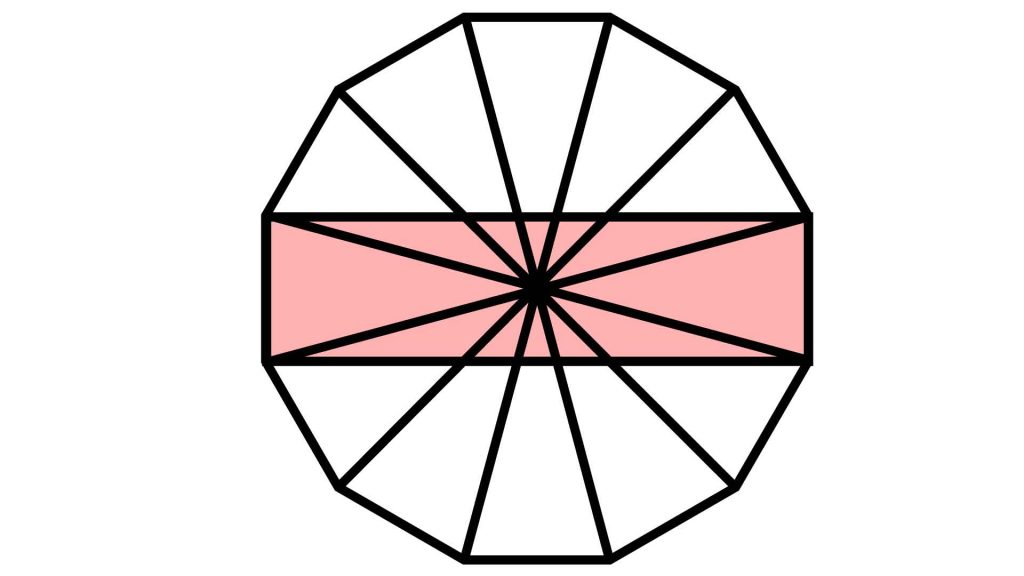
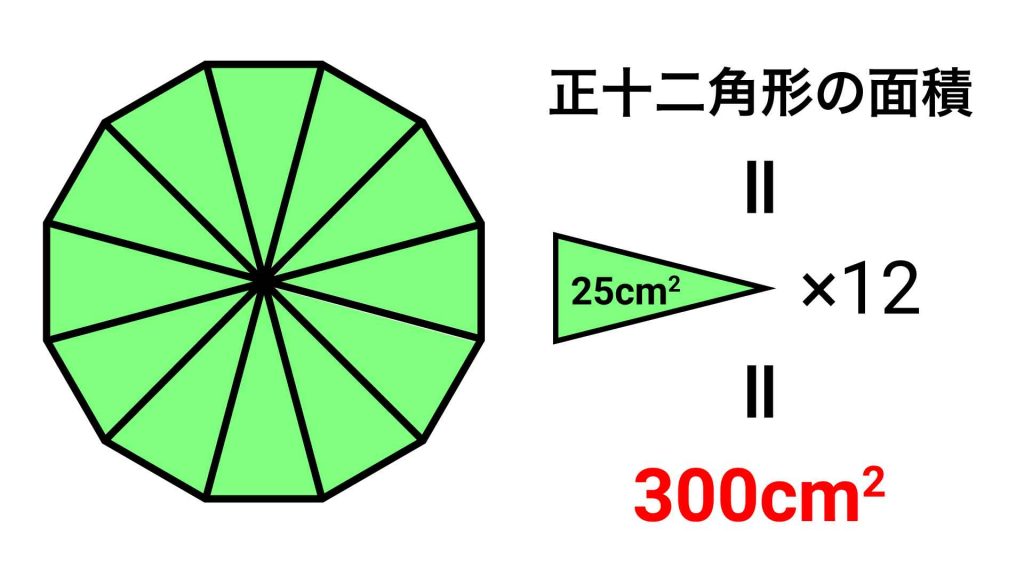
この図は、正十二角形の1つの頂点と、それと点対称な位置にある頂点を結び、12個の三角形に分割したものです。
実は、この操作を行ってできる12個の三角形の面積は、すべて等しくなります。
▲右の図がキウイの断面に見えますね
したがって、緑色の三角形1つ分の面積をどうにかして求め、それを12倍すれば、正十二角形の面積を求めることができます。
緑色の三角形1つ分の面積を求めるのに、赤色の長方形の面積の情報が必要になります。
その方法をこれから解説していきます！
赤色の長方形、対角線を2本引くと……？
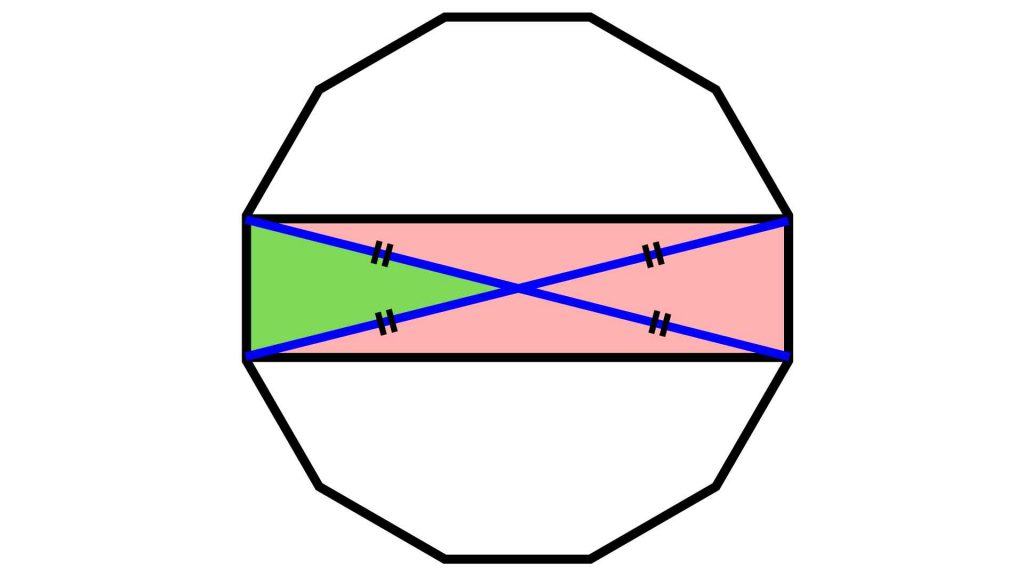
緑色の三角形は、赤い長方形の対角線を2本引くと現れます。
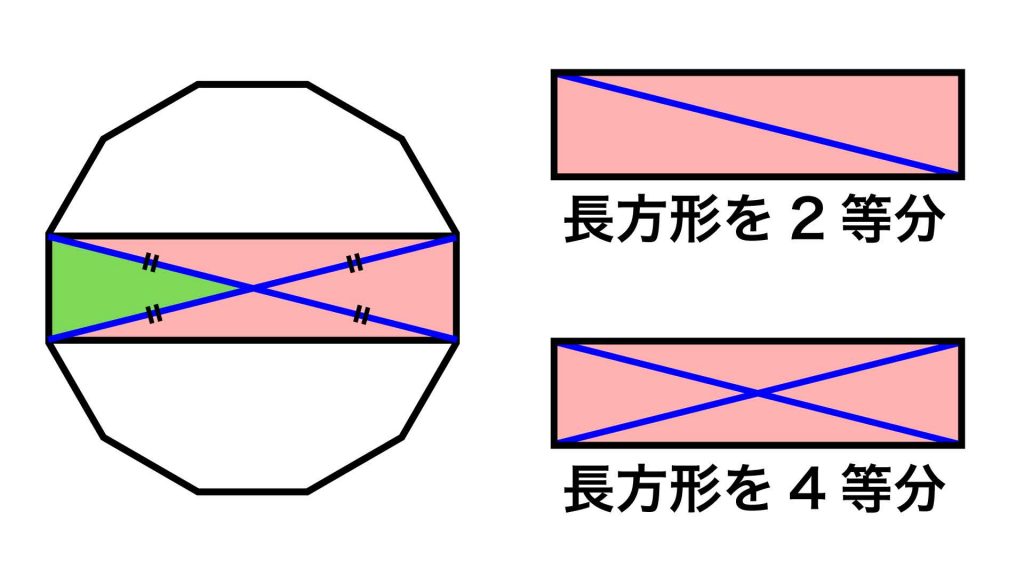
ここで、本問題を解く上で非常に重要となる性質を使います。それは、「長方形の対角線を2本引くと、長方形の面積は4等分される」ということです。
1本引くと2等分され、さらにもう1本引くと4等分されます！ 4等分ということは……？
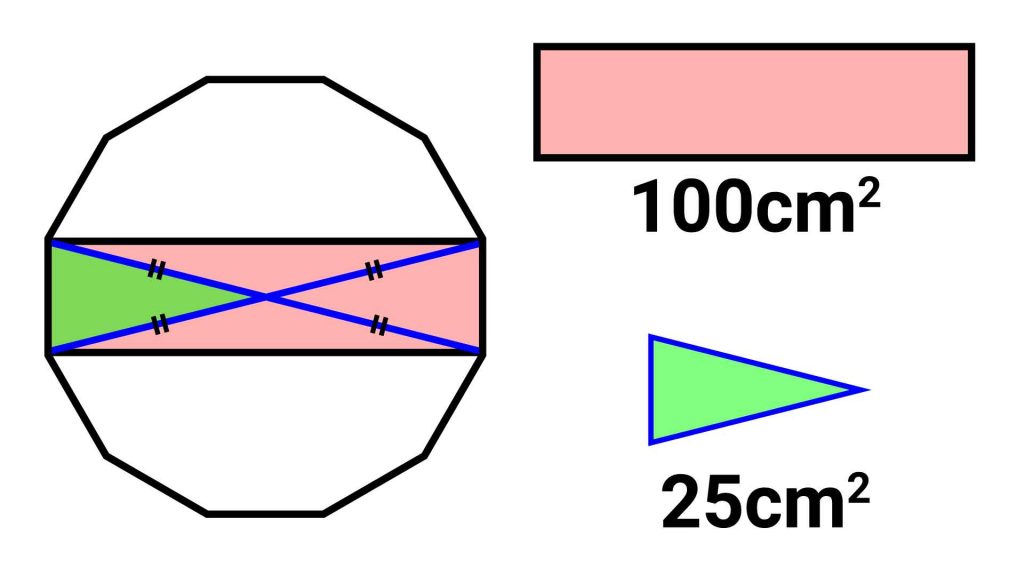
赤色の長方形の面積が100cm2なので、対角線によって分けられた4つの三角形の面積はすべて100÷4=25cm2となります。
したがって、緑色の三角形の面積は、25cm2となります。
正十二角形の面積は、緑色の三角形の面積の12個分なので、答えは25×12=300cm2となります。
答え：300cm2
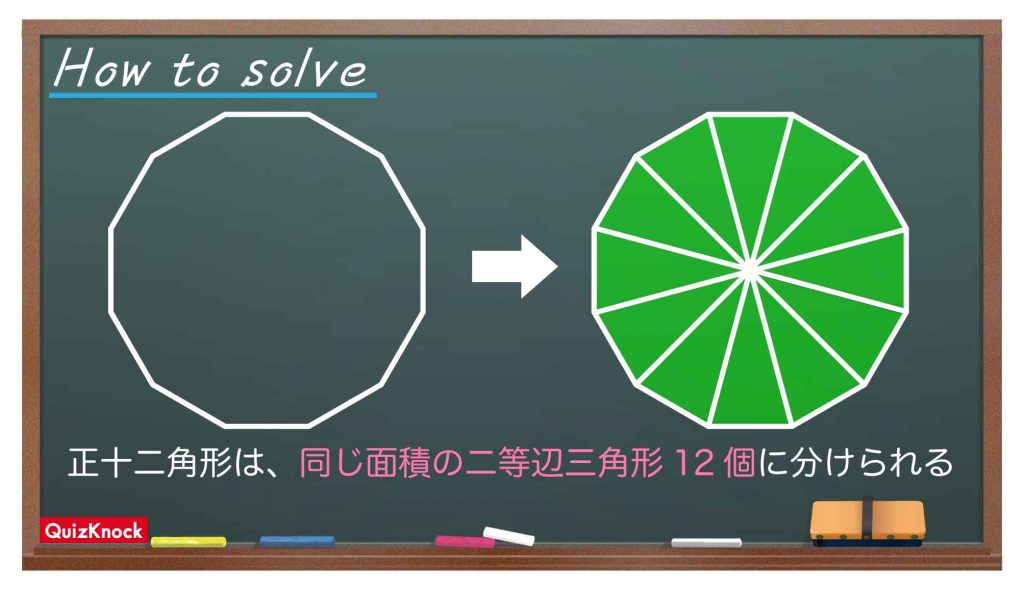
正十二角形が、同じ面積の三角形12個からできていることに気づけるかどうかがポイントでした。
それでは。
「ひらめけ！算数ノート」のバックナンバーはこちらから！
【前回の算数ノートはこちら】
【あわせて読みたい】
