解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回の問題のポイントは、連続する自然数の和を、最小の数と最大の数を順に足して求めることです。
このポイントを頭に入れて、解いていきましょう!
1から20までの和は?
まずは、1から20までの自然数の和を求めます。ここでは、自然数を順に足し上げていくよりも簡単な求め方を紹介します。
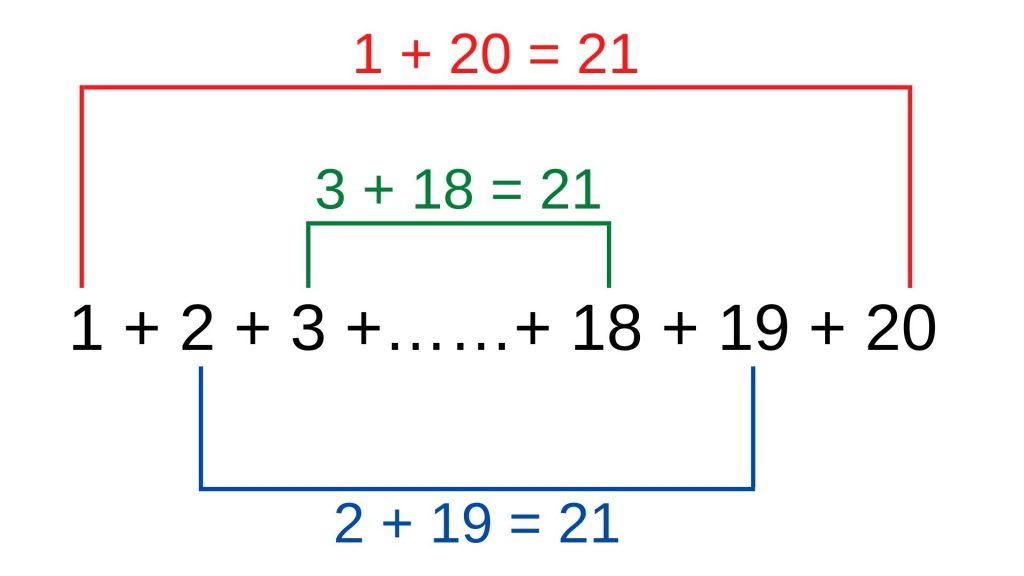
1から20までの自然数のうち、最も小さい1と最も大きい20を足すと、1+20=21となります。
次に、残った2から19までの自然数のうち、最も小さい2と最も大きい19を足すと、2+19=21となります。
これを繰り返すと、足して21になる自然数の組が10組できることがわかります。
したがって、1から20までの自然数の和は、21×10=210となります。
和を750にするには?
ここからは、1から20までの自然数にそれぞれ同じ数だけ足すことで、和を750にすることを考えます。
1から20までの自然数の和が210であり、これと750との差を求めると、750-210=540となります。
つまり、1から20までの自然数にそれぞれ、540÷20=27だけ足せば、和が750になります。
したがって、最も小さい自然数は1+27=28です。
答え:28
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】












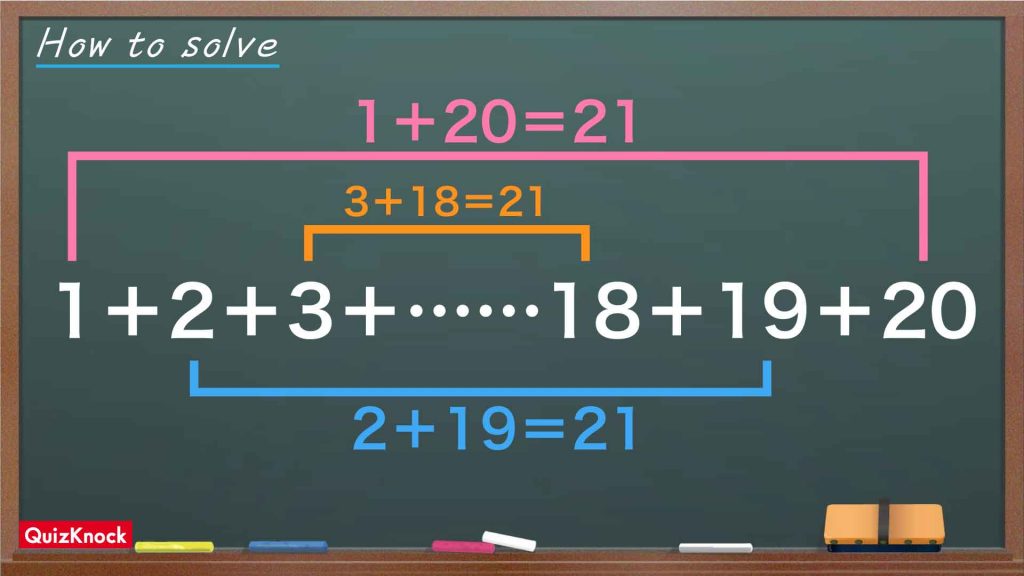
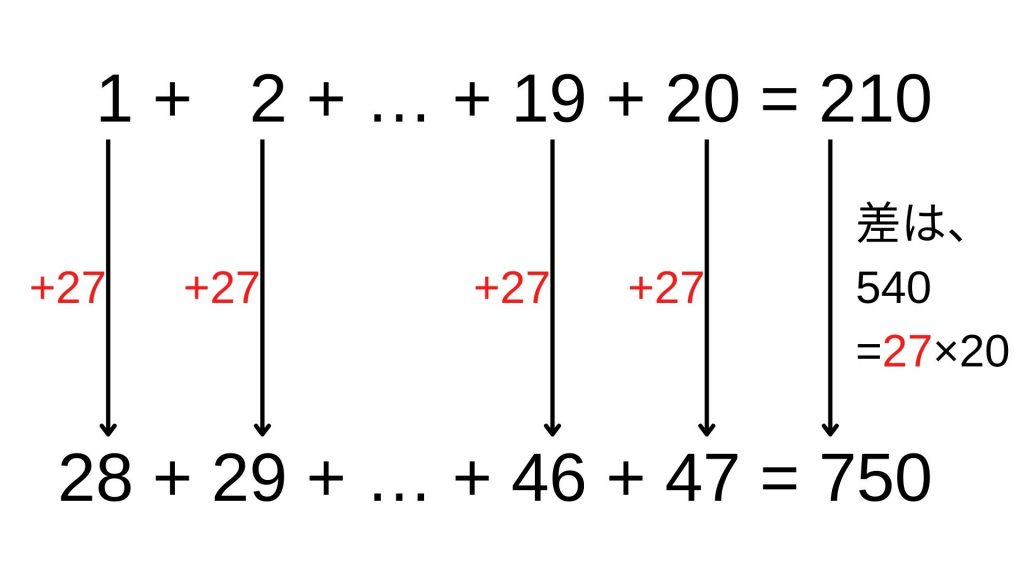
.jpg)







.jpg)







