解説
それでは解説です。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回のポイントは、「合同な三角形を見つける」ことです。
「合同」とは、「2つの図形がぴったりと重なりあう」関係のこと。三角形の場合、以下の3種類の条件のうちどれかを満たしていれば合同といえます。
以上を踏まえ、問題を解いていきましょう!
等しい角を見つける
まず、下図で緑とピンク色で示した2つの角に着目します。
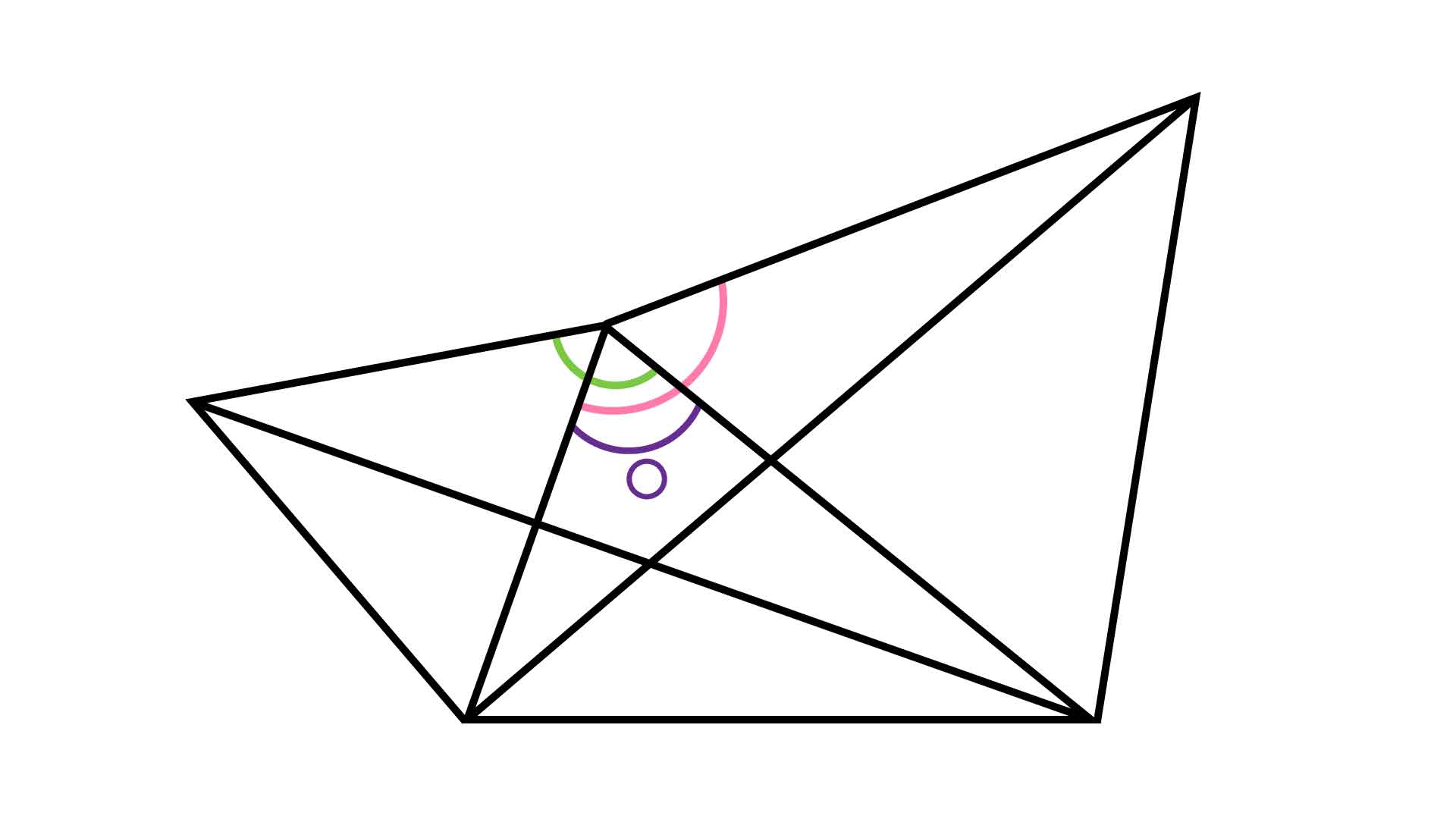
正三角形における1つの角の大きさは60度です。緑とピンクの角が重なっている角の大きさを「〇」とすると、どちらも大きさは「〇+60」度となり、2角が等しい大きさをもつことがわかります。
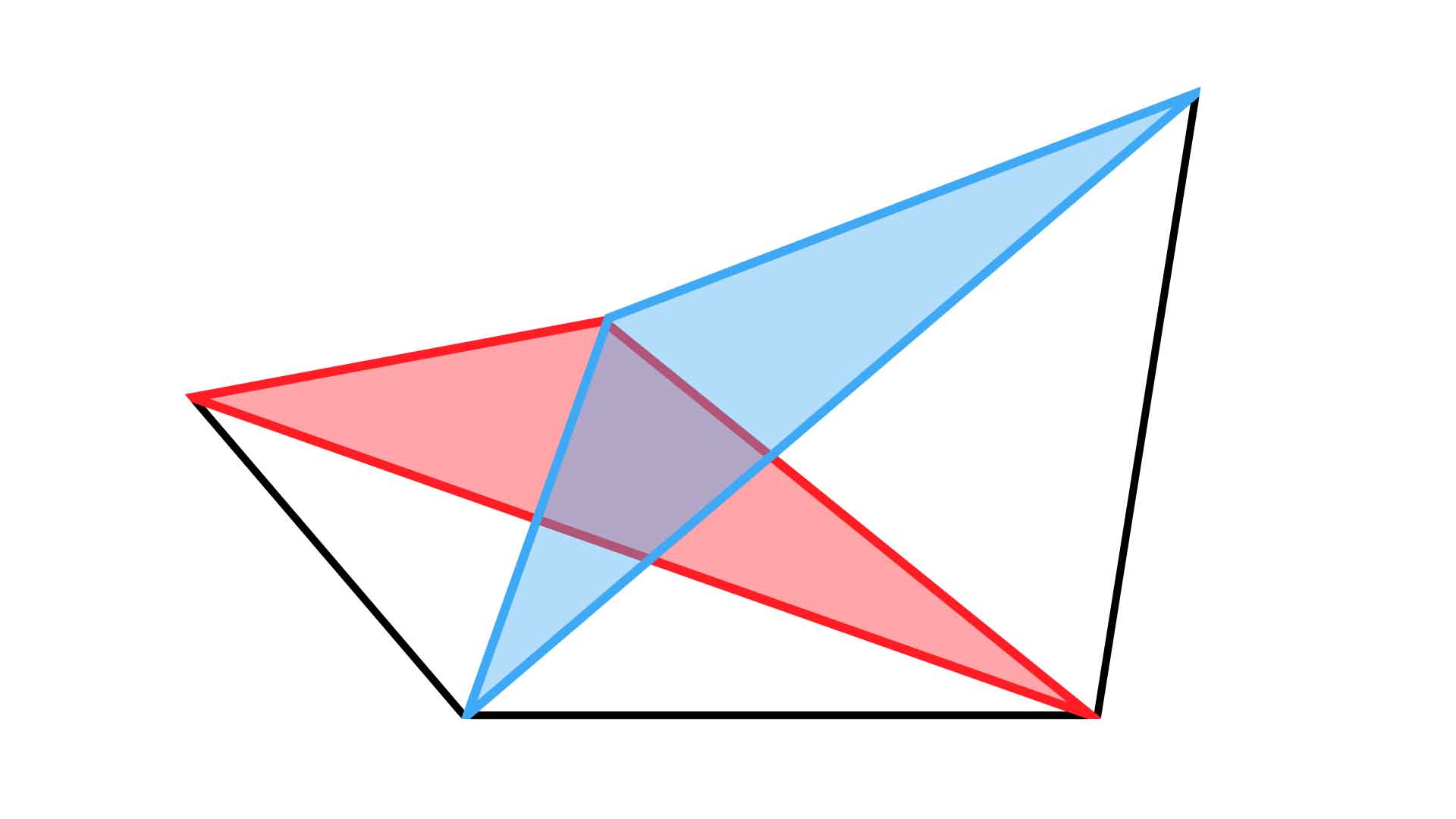
合同な三角形を見つける
この等しい2角と、正三角形がもつ等しい長さの辺を利用すると、1組の合同な三角形が浮かび上がってきます。
合同な三角形の内角を利用する
次に、合同な1組の三角形の右側にある角(下図でピンク色で示した角)の大きさを「X」と置きます。そして、下の図で緑色で示した三角形に着目してみてください。
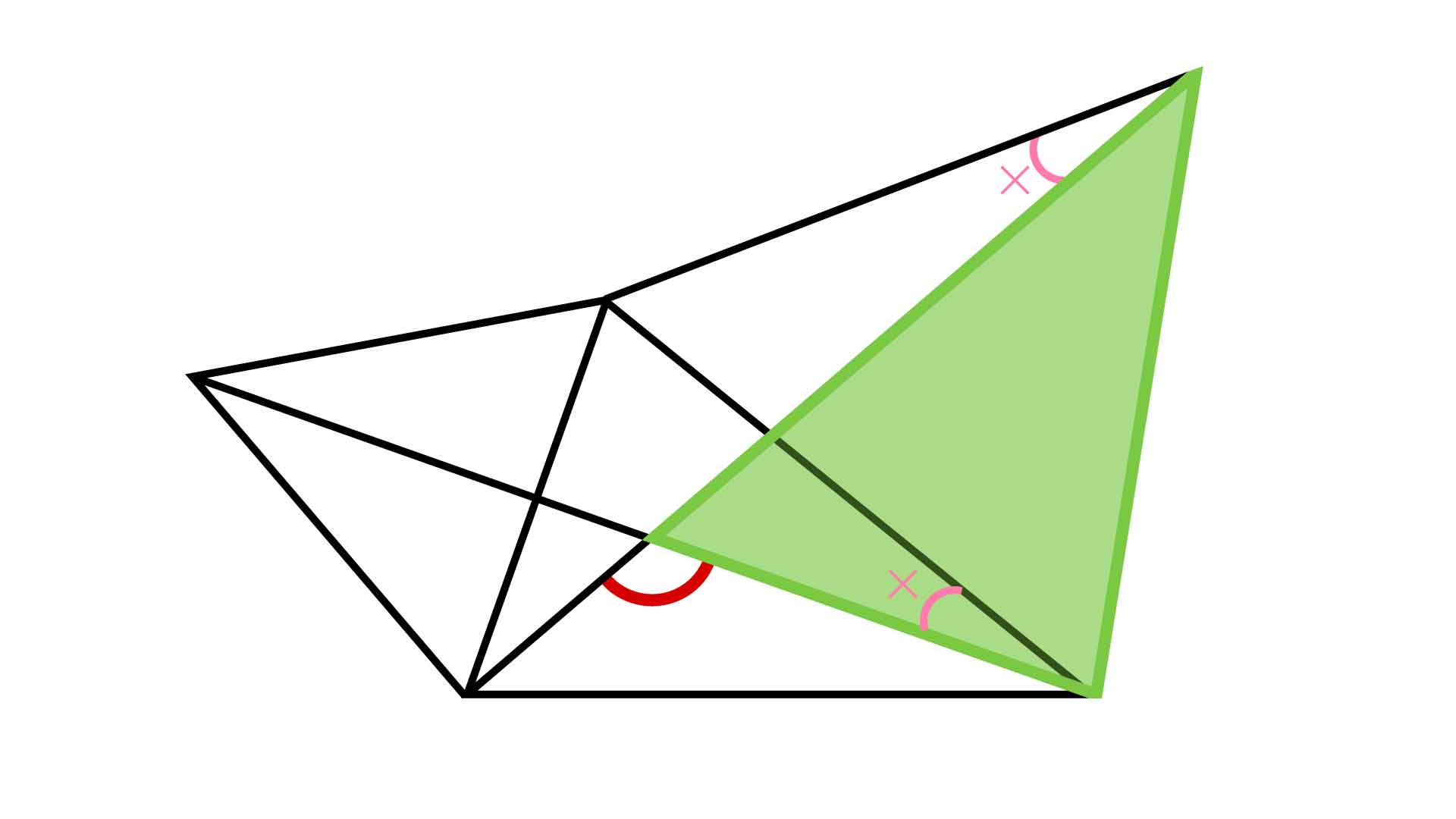
この三角形の上側の角の大きさは「60-X」度、下側の角の大きさは「60+X」度であることがわかります。つまり、上下の角を足すと、60-X+60+X=120度になります。すると、残りの内角の大きさは180-120=60度となります。
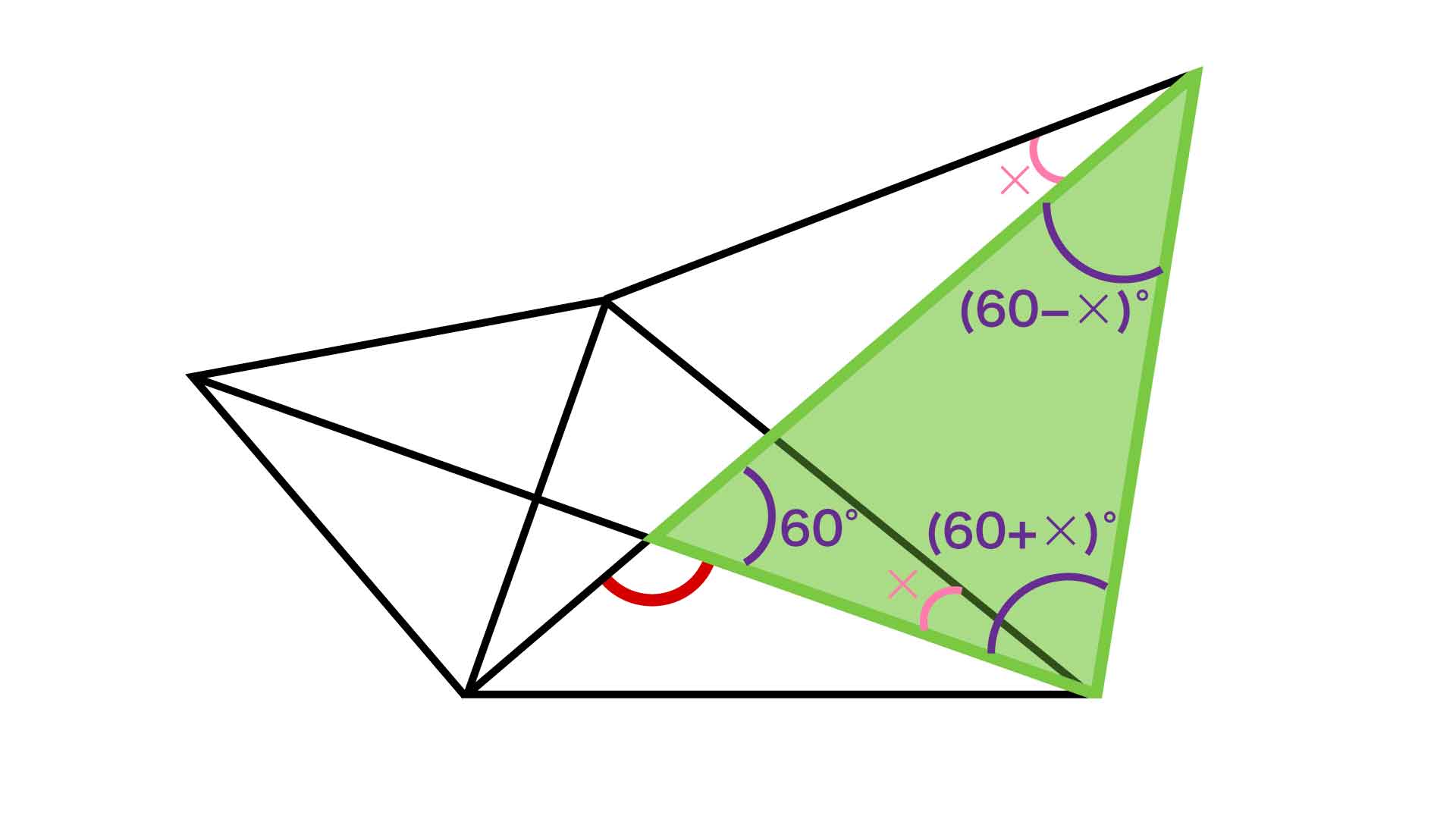
よって、求める角はこの60度の角に隣接しているので、その大きさは180-60=120度となります。
答え:120度


















.jpg)







