解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
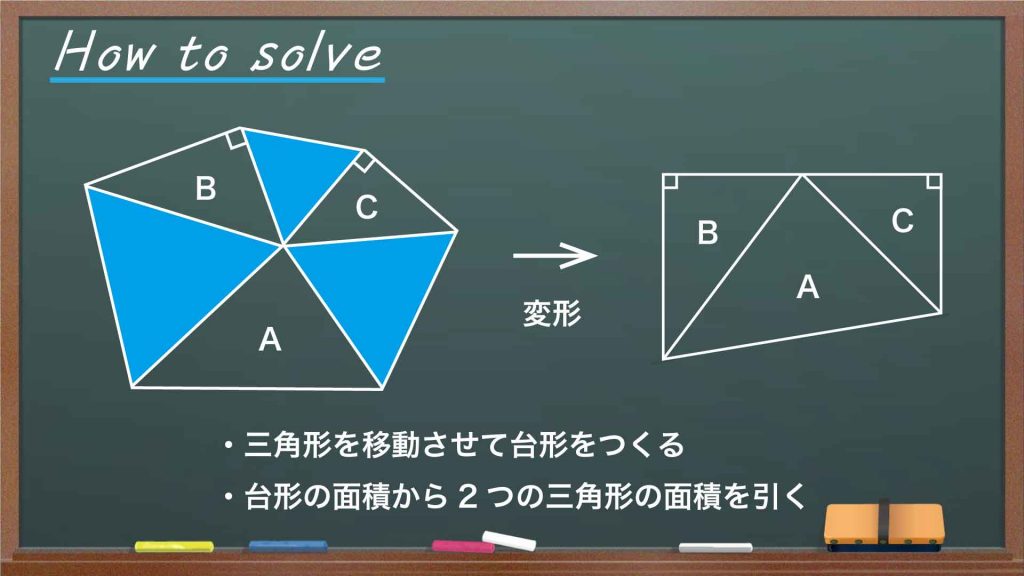
今回の解き方をまとめた図がこちらです。
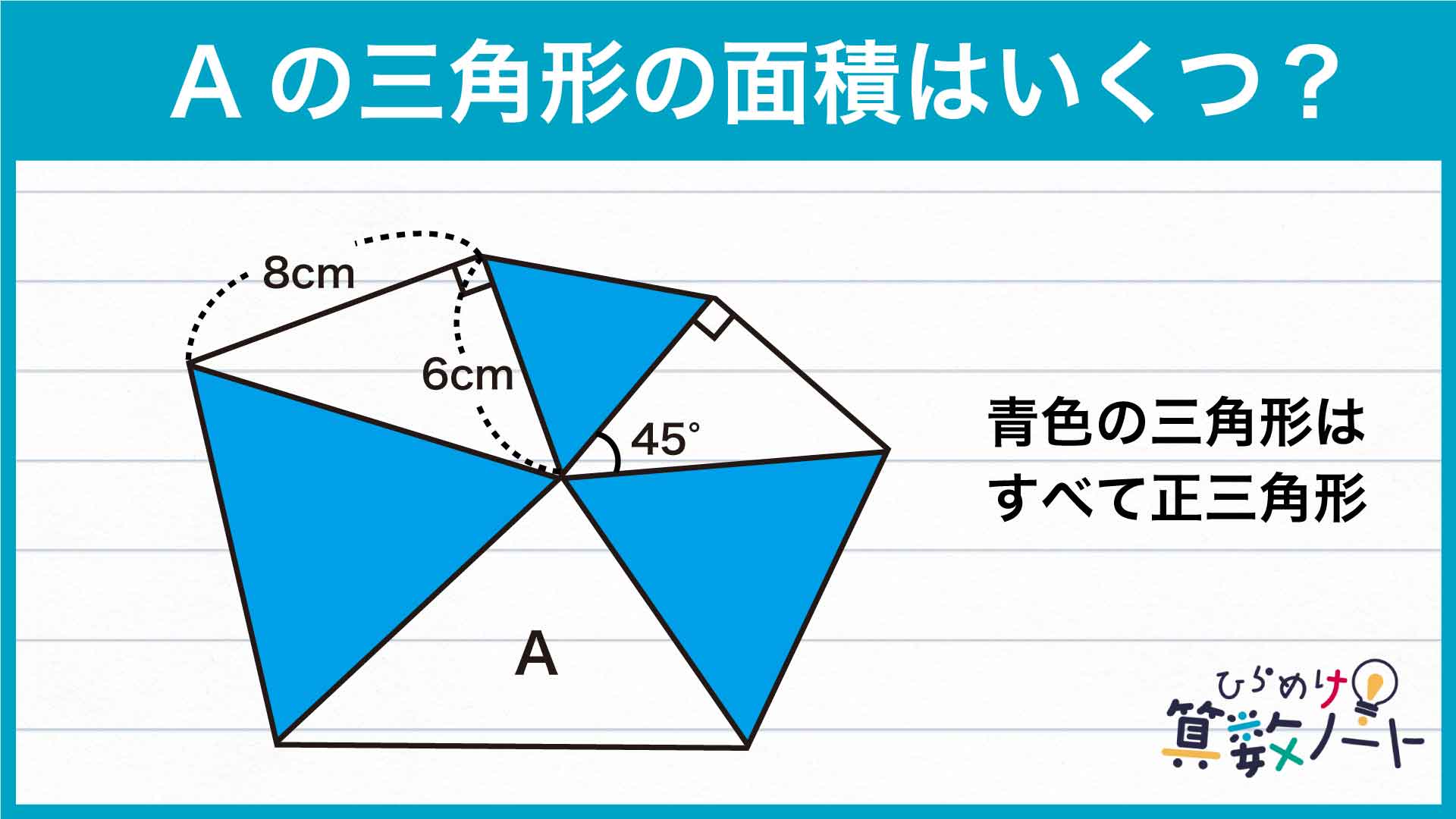
今回の問題のポイントは、正三角形の性質を利用して「面積を求めやすい図形を作る」ことです。
この流れに沿って、問題を攻略していきましょう!
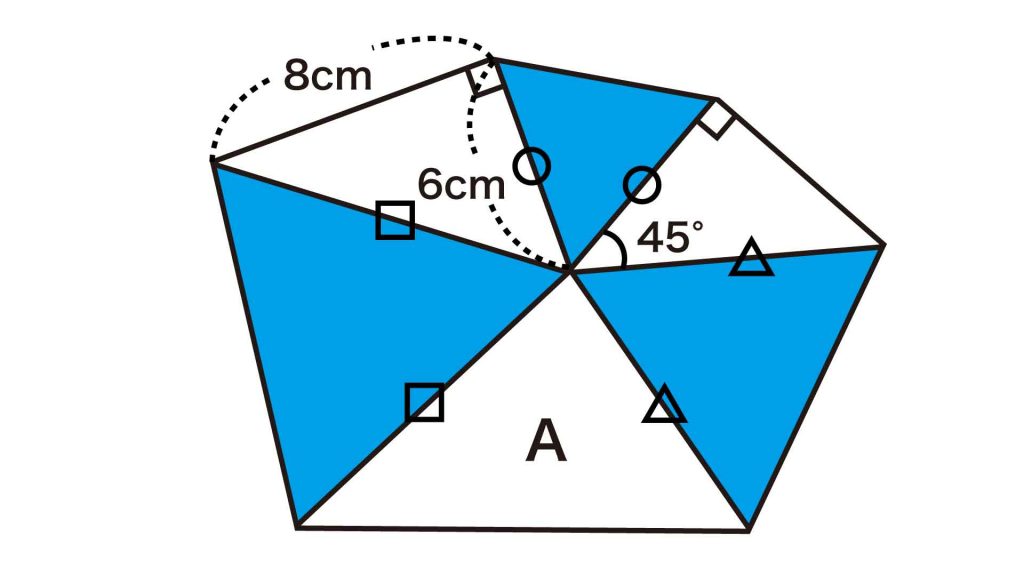
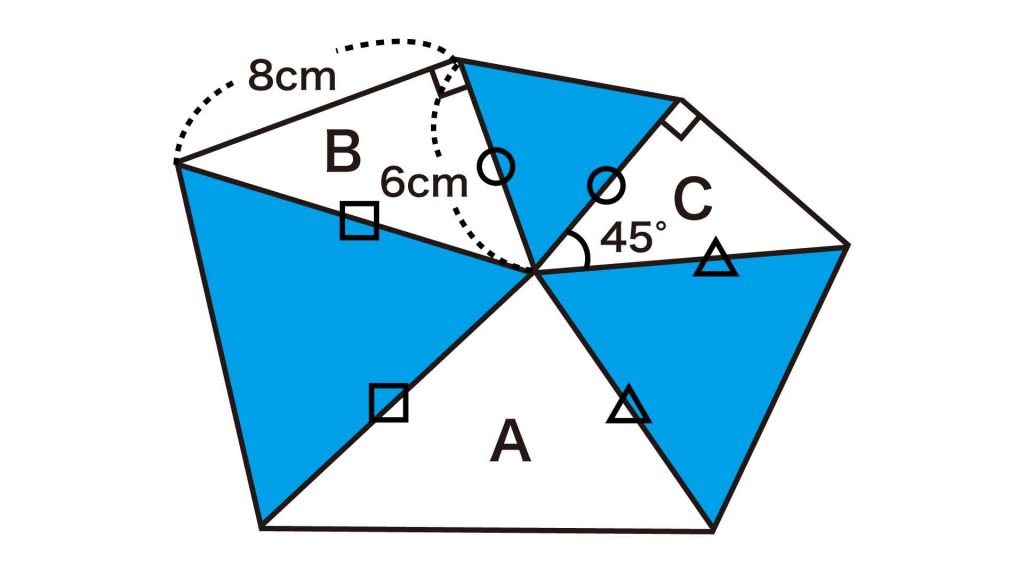
辺の長さが等しい→ぴったりとくっつく
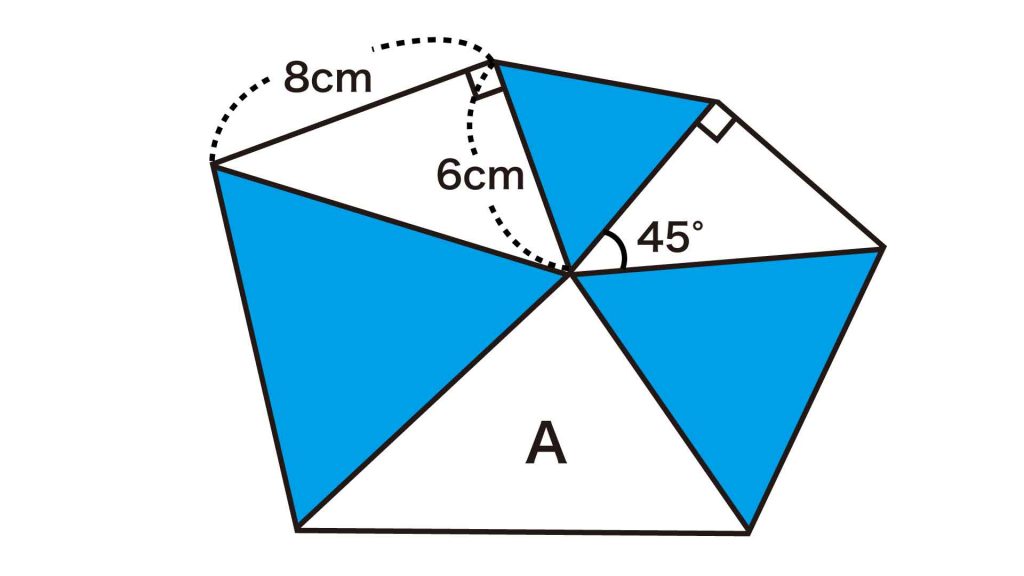
青色の三角形はすべて正三角形なので、下の図で◯、△、□で示した辺の長さはそれぞれ等しいです。
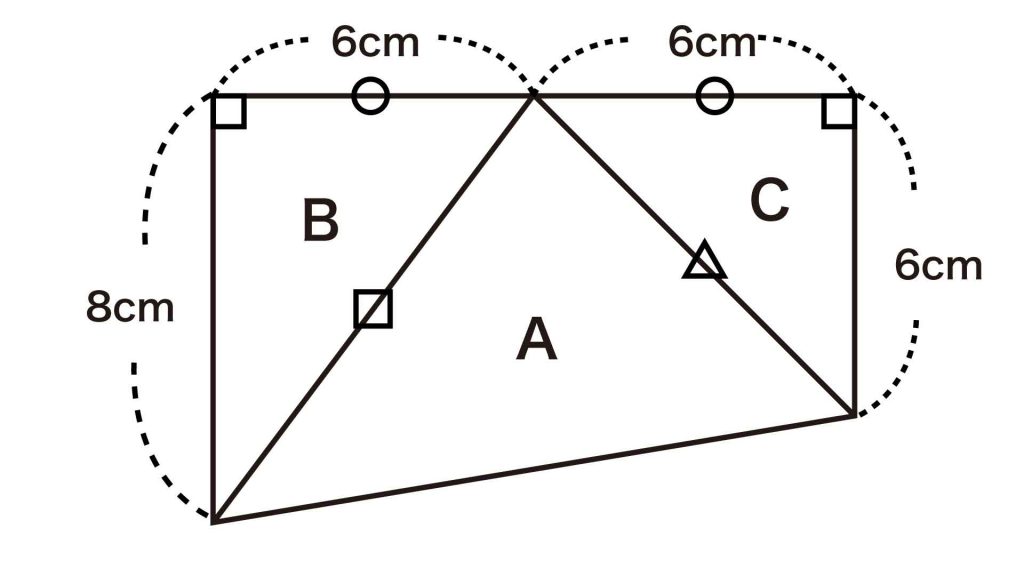
ここで、下の図のように、2つの白い直角三角形をそれぞれB、Cとします。
B、Cはそれぞれ、斜辺の長さがAの一辺の長さと等しいので、下の図のようにぴったりとくっつけることができます。
図形の性質を調べる
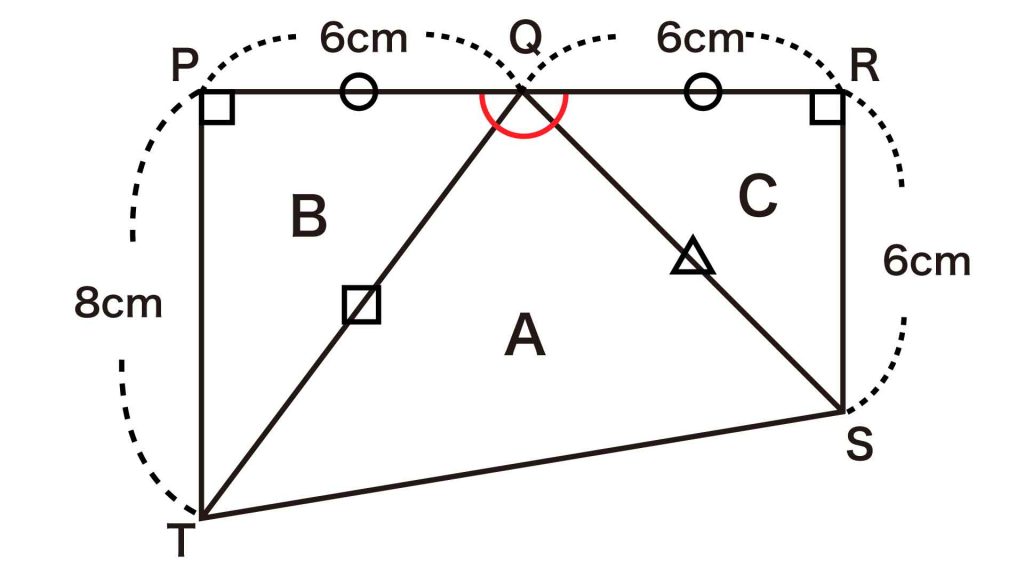
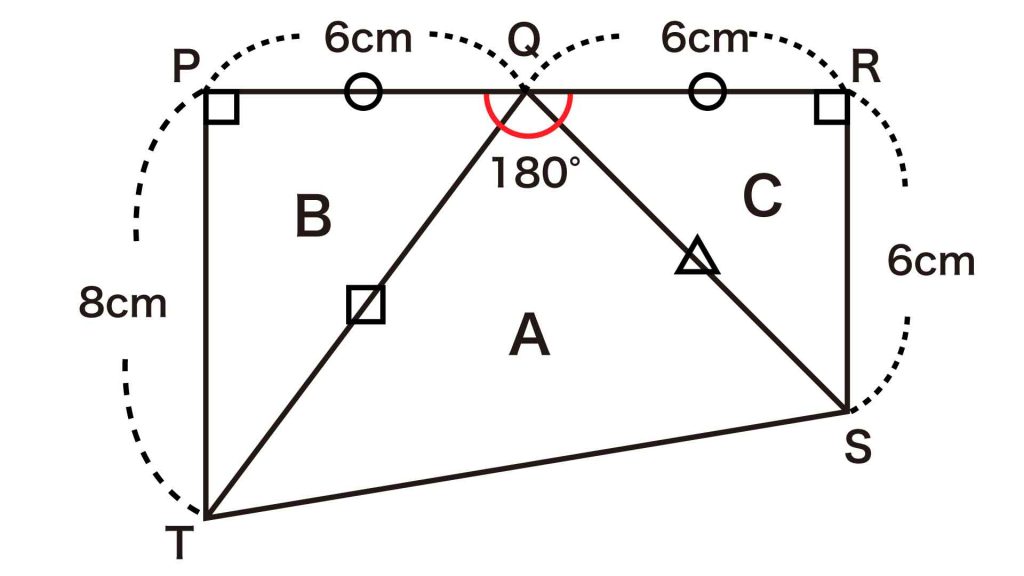
A、B、Cの3つの三角形を組み合わせてできた図形について、下の図のように各点をP、Q、R、S、Tとおき、角PQRの大きさについて考えます。
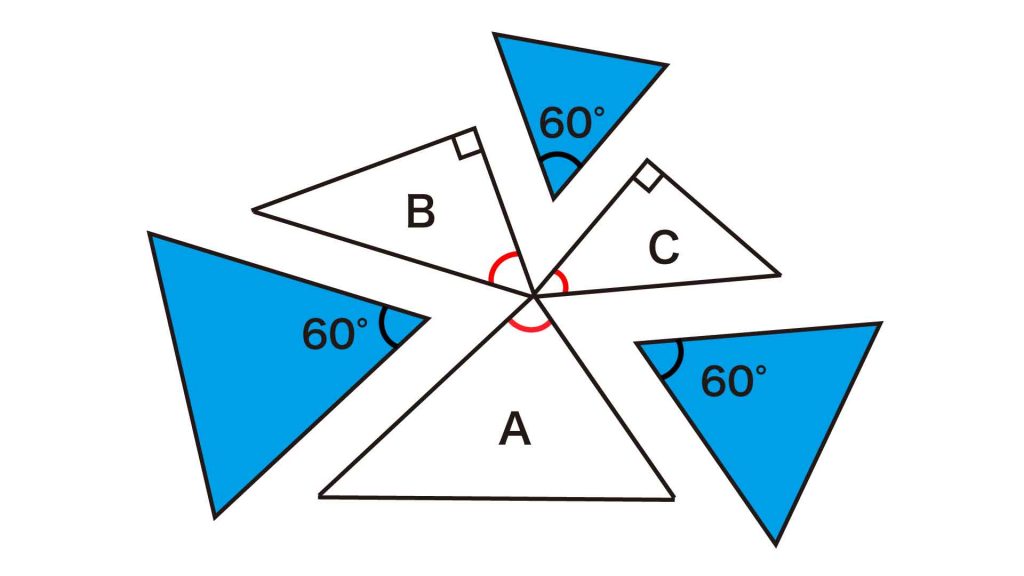
角PQRは、もとの図形において6つの三角形の頂点が集まってできた角から、正三角形の内角3つ分を除いた角です。
正三角形の内角の大きさは60度なので、角PQRの大きさは、360-(60×3)=180度となります。したがって、3つの点P、Q、Rは、一直線上に並んでいることがわかります。
また、最初の条件より、角TPR=角SRP=90度です。
以上より、3つの白色の三角形A、B、Cを組み合わせた図形は、台形であることがわかります。
Aの面積を求める
Aの面積は、台形の面積からBとCの面積を引くことで求めることができます。
台形は、2つの底辺の長さがそれぞれ6cmと8cm、高さは12cmなので、面積は、(6+8)×12÷2=84cm2となります。
続いて、BとCの面積を求めます。
Bは底辺8cm、高さ6cmの直角三角形なので、面積は、8×6÷2=24cm2となります。
またCは、角RQSの大きさが45度であることから直角二等辺三角形であり、RQ=RS=6cmなので、面積は、6×6÷2=18cm2となります。
以上より、Aの面積は、84-(24+18)=42cm2となります。
答え:42cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)










.jpg)







