【問題はこちら】
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
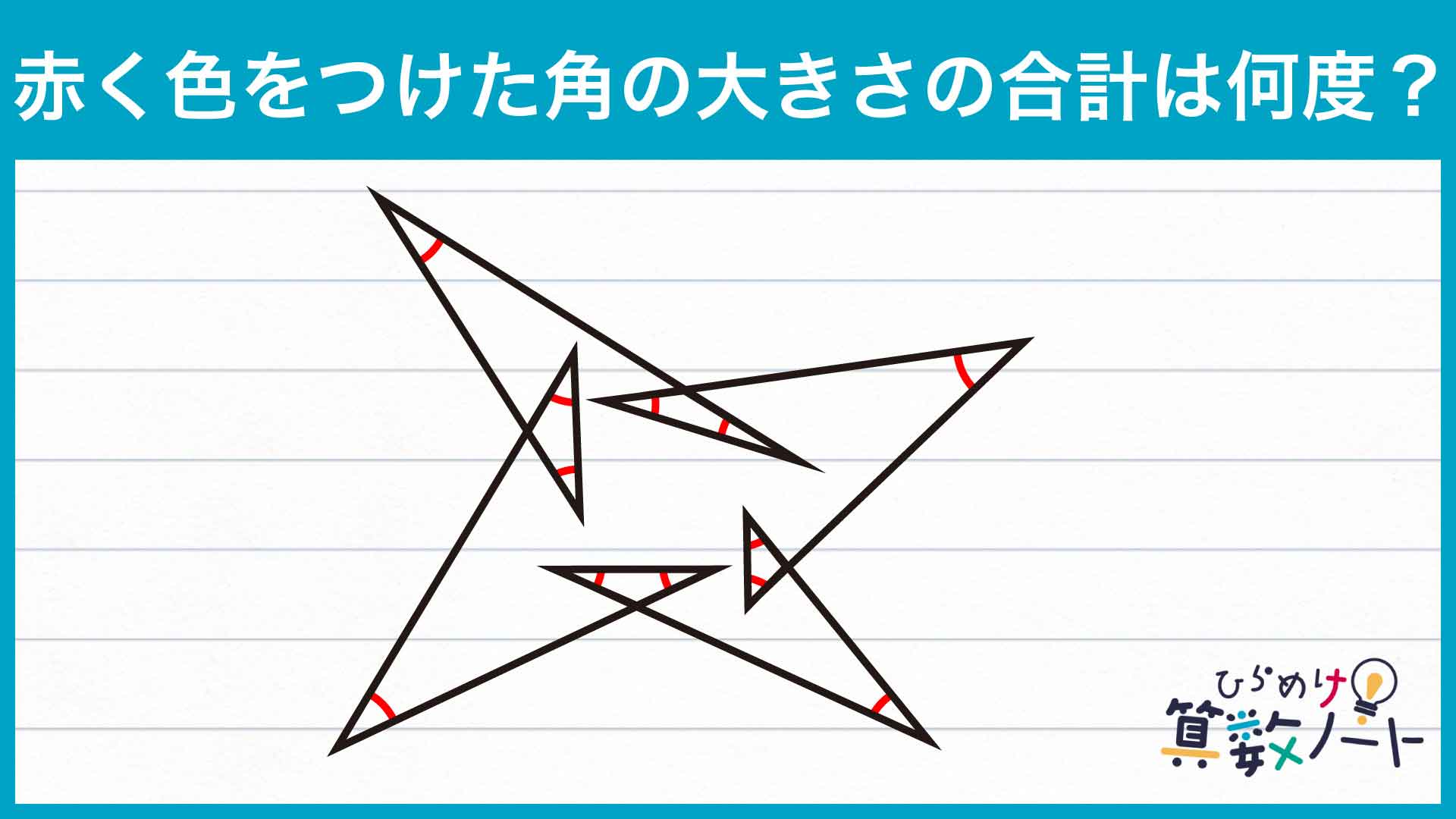
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらです。
ポイントは、砂時計の形に注目して、複数の角を大きさの等しい別の角に移動させることです。これを踏まえて解いていきましょう!
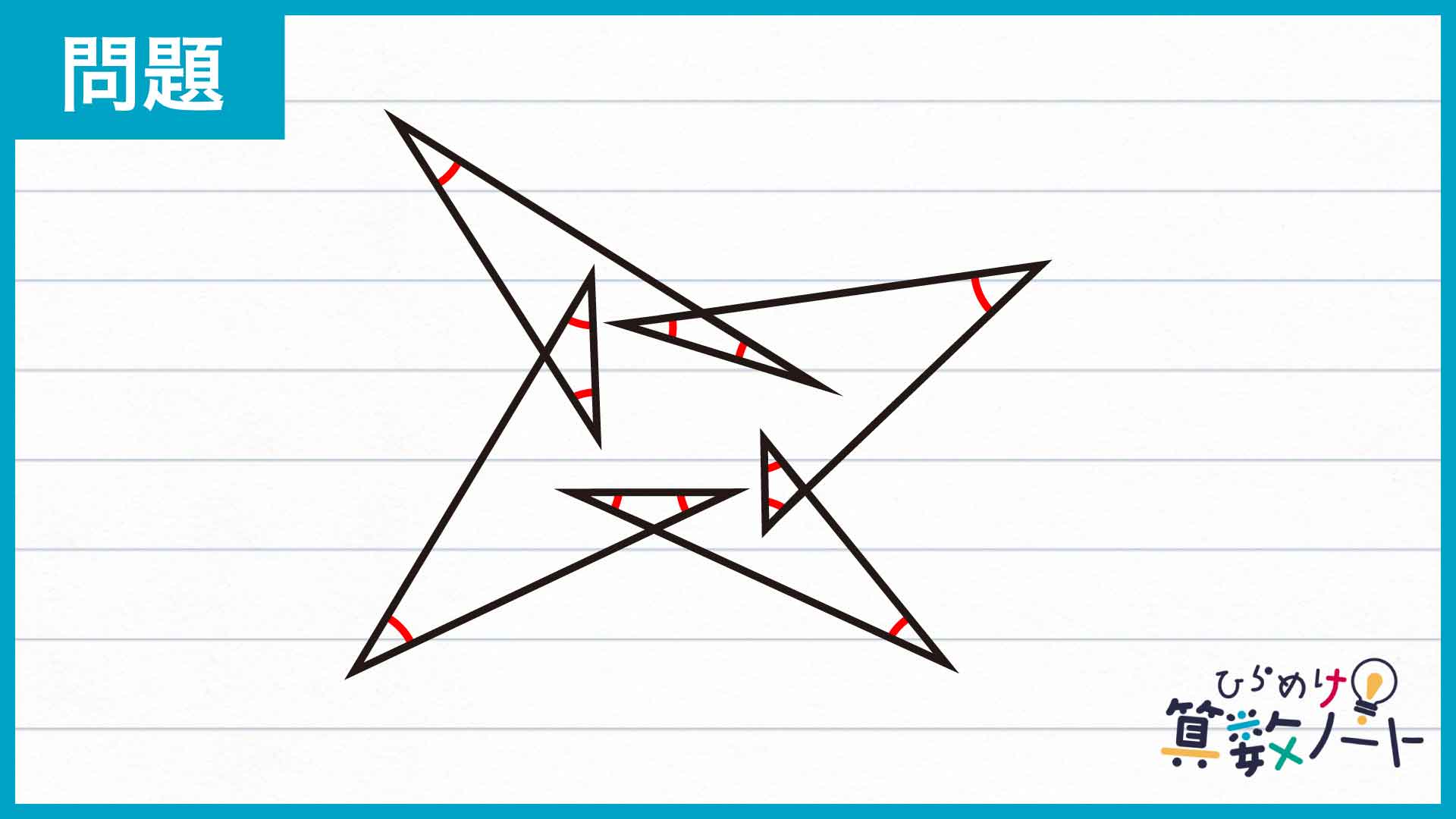
補助線を引く
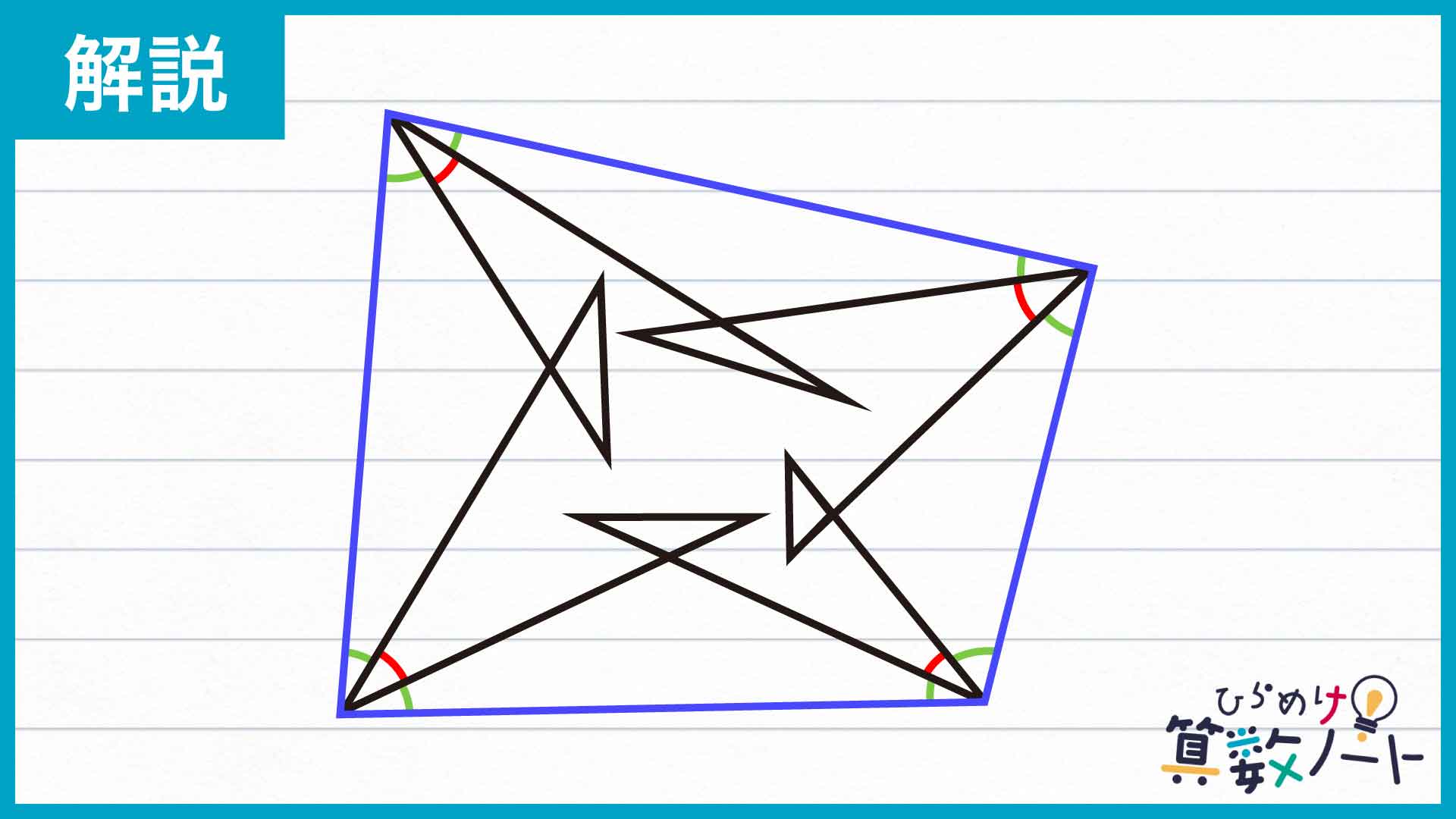
下の図のように、大きな四角形ができるよう4本の補助線を引きます。
赤い色をつけたそれぞれの角の大きさはわからないため、角の大きさを1つずつ足して答えを求めることはできません。しかし、たとえば「三角形の内角の大きさの和は180度」というように、それぞれの角の大きさがわからなくても、その合計が求められる場合があります。これらの補助線は、そのような形を目指して引いたものです。
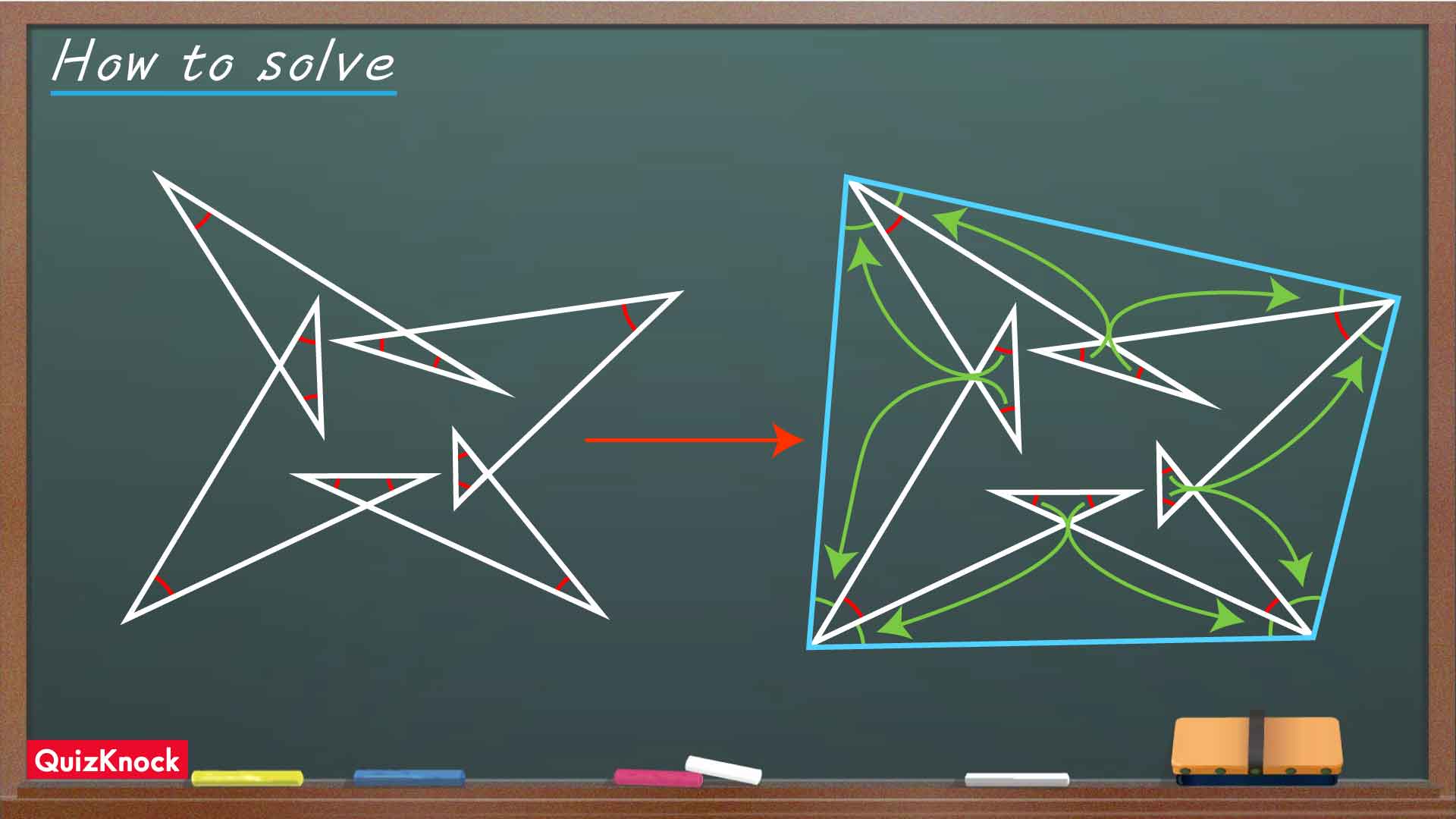
「砂時計の形」に注目して角を移動する
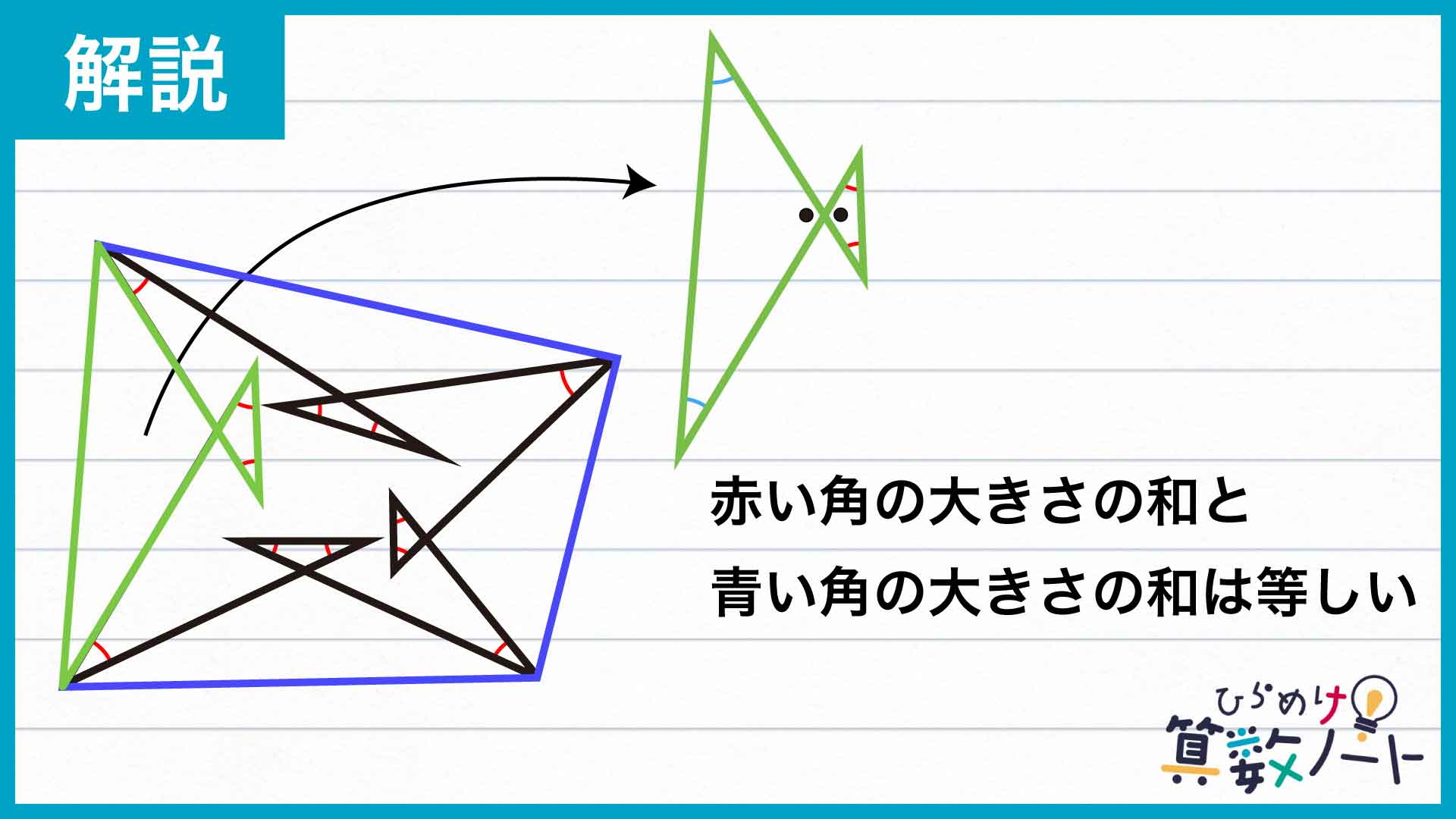
ここで、緑色の部分に注目します。この部分は2つの三角形が向かい合って砂時計のような形になっています。この2つの三角形において、●をつけた部分は対頂角(2本の直線が交わってできる角のうち、互いに向かい合っているもの)の関係にあるため大きさが等しいです。三角形の内角の大きさの和は180度なので、2つの三角形の、●をつけた角以外の2つの角の大きさの和は等しくなります。
このような「砂時計の形」が4カ所あるので、それぞれにおいて2つの角を、大きさの和が等しい2つの角に移動させることができます。
角の大きさの和を求める
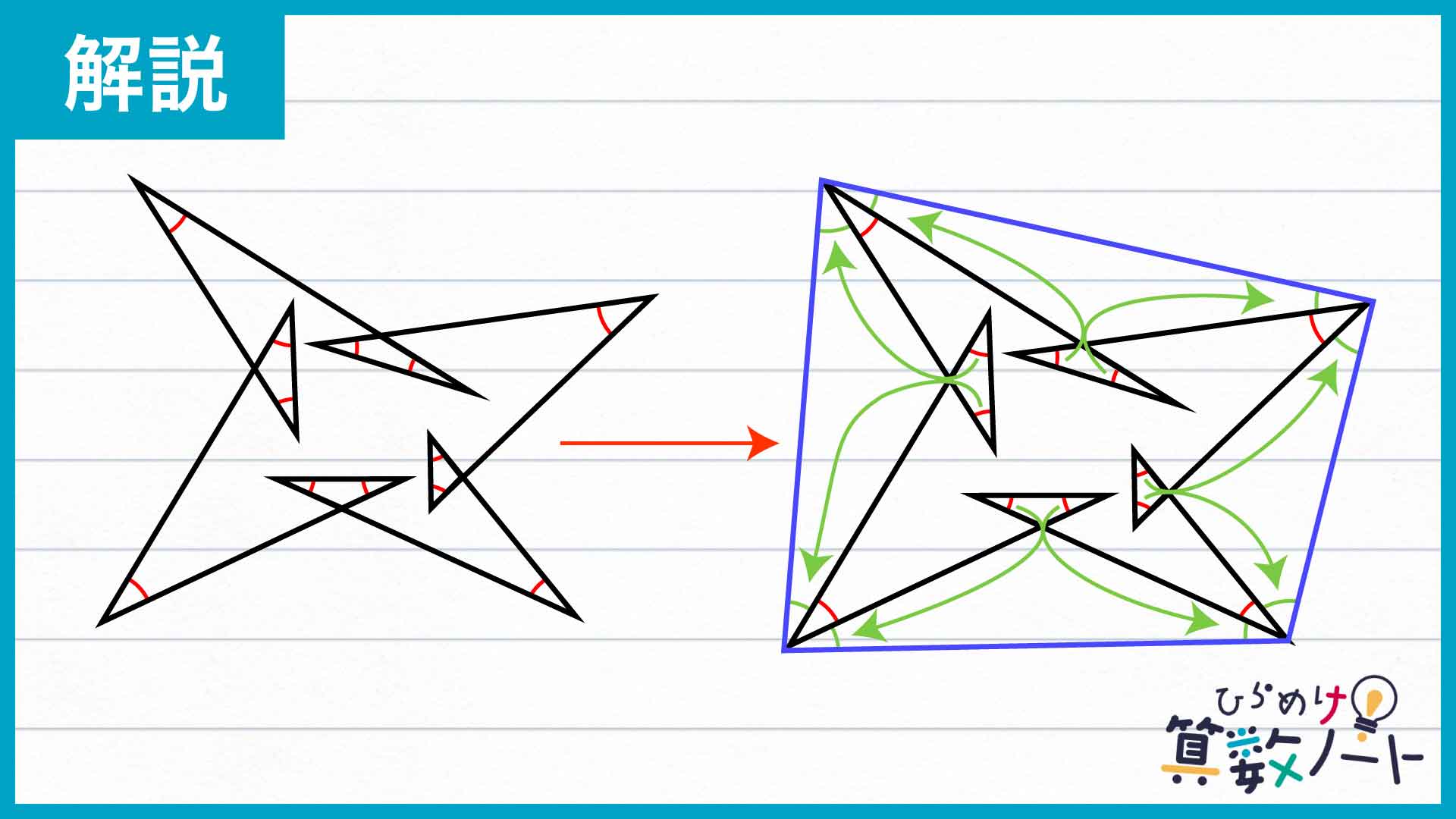
このように角を移動させると、図は下のようになります。
求める角度の和は、青い色をつけた四角形の内角の大きさの和と同じなので、答えは360度になります。
答え:360度それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)








.jpg)






