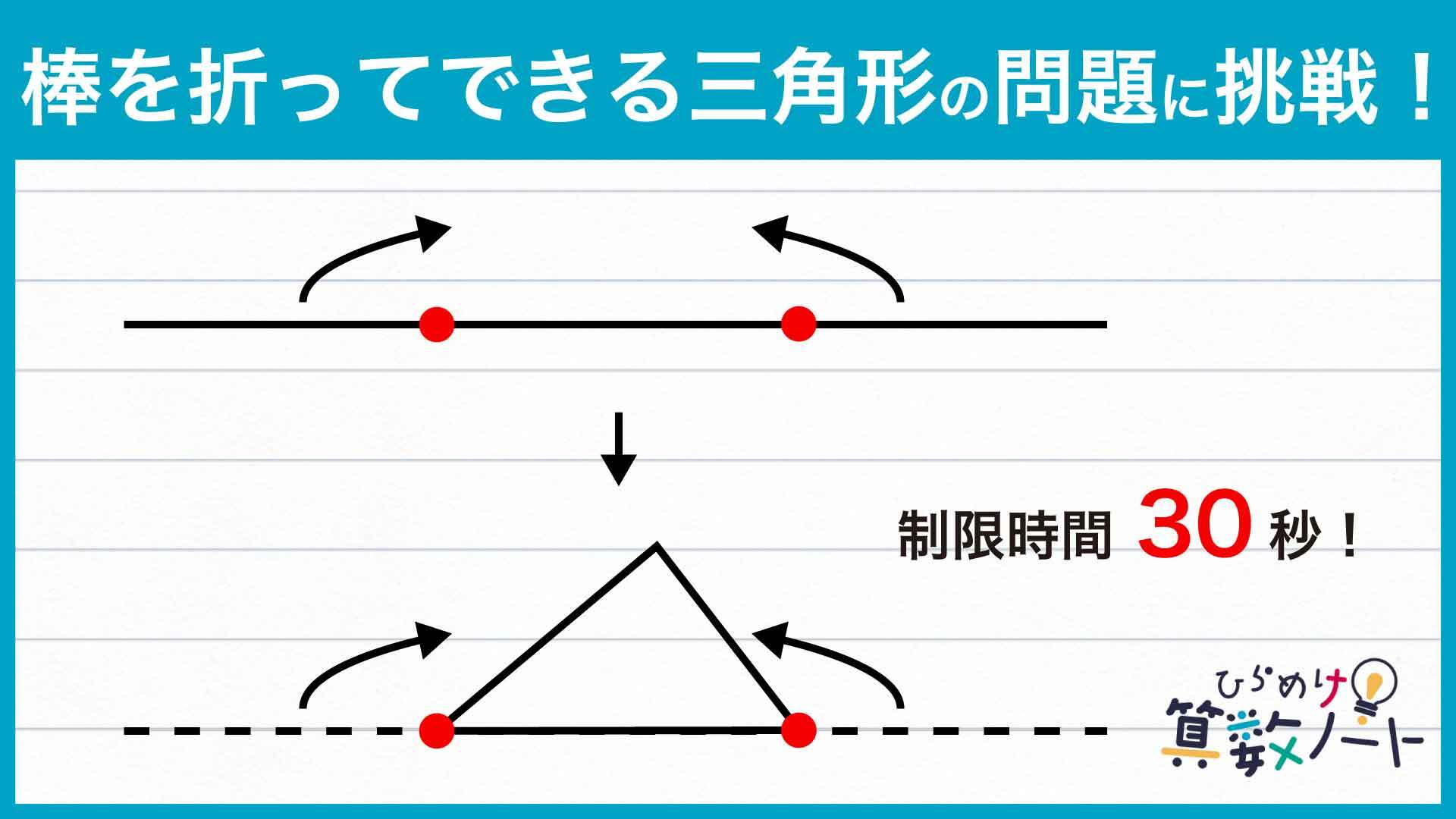
例題はこちら
1ページ:【30秒以内に解ける?】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
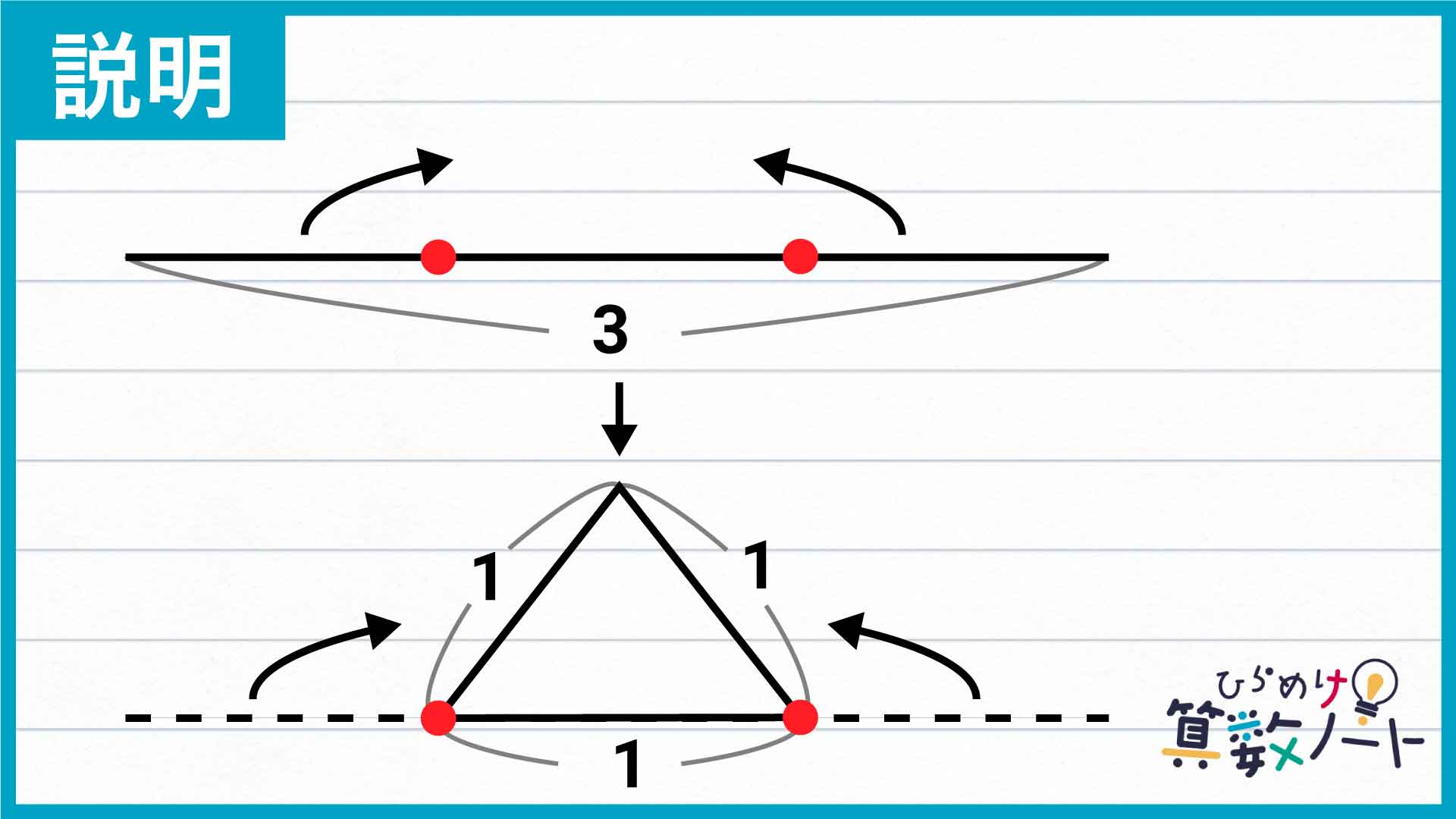
この問題の解き方をまとめた図がこちらです。
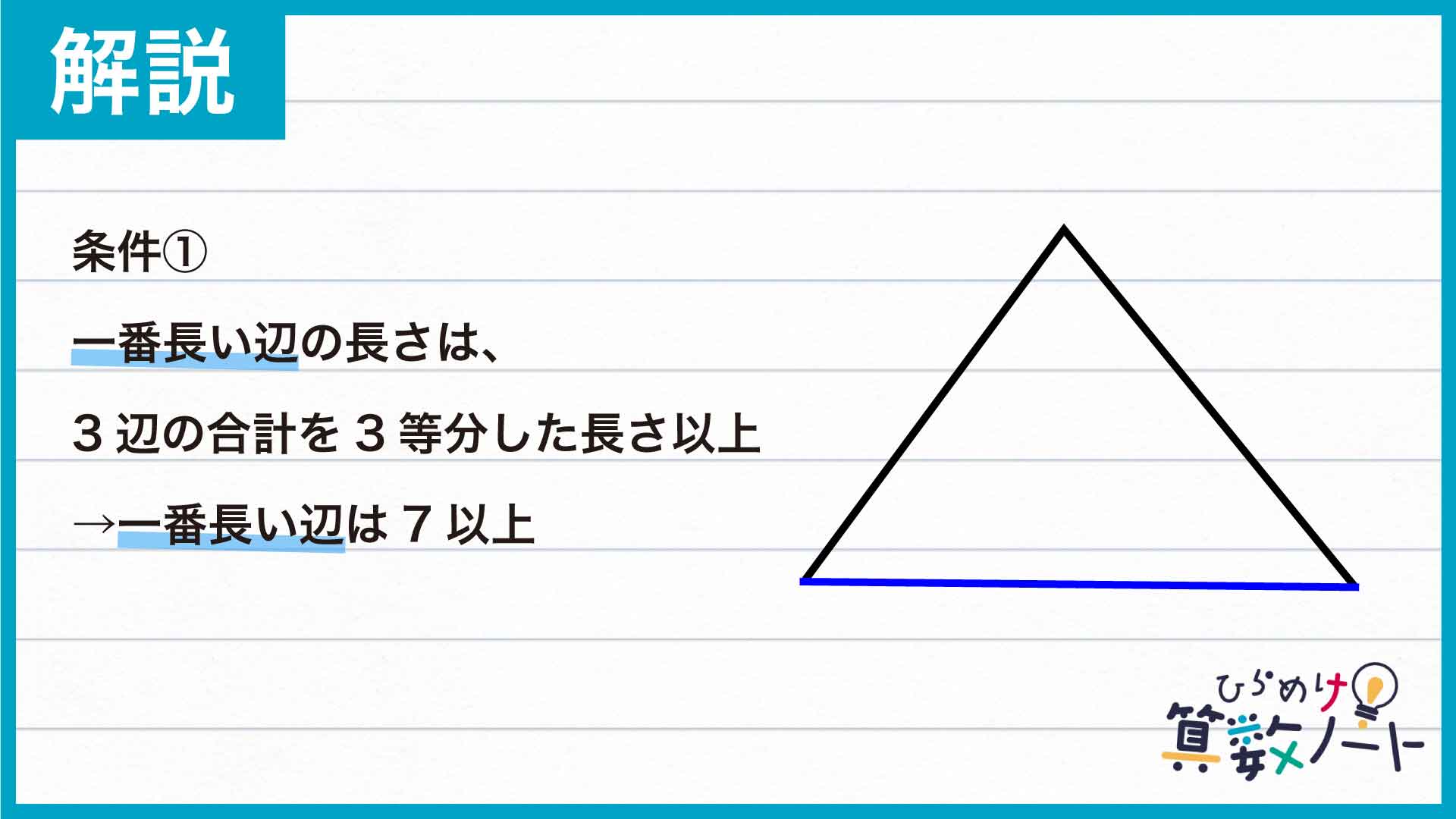
ポイントは、一番長い辺が満たすべき条件を考えることです。
では、このポイントを踏まえつつ解いていきましょう!
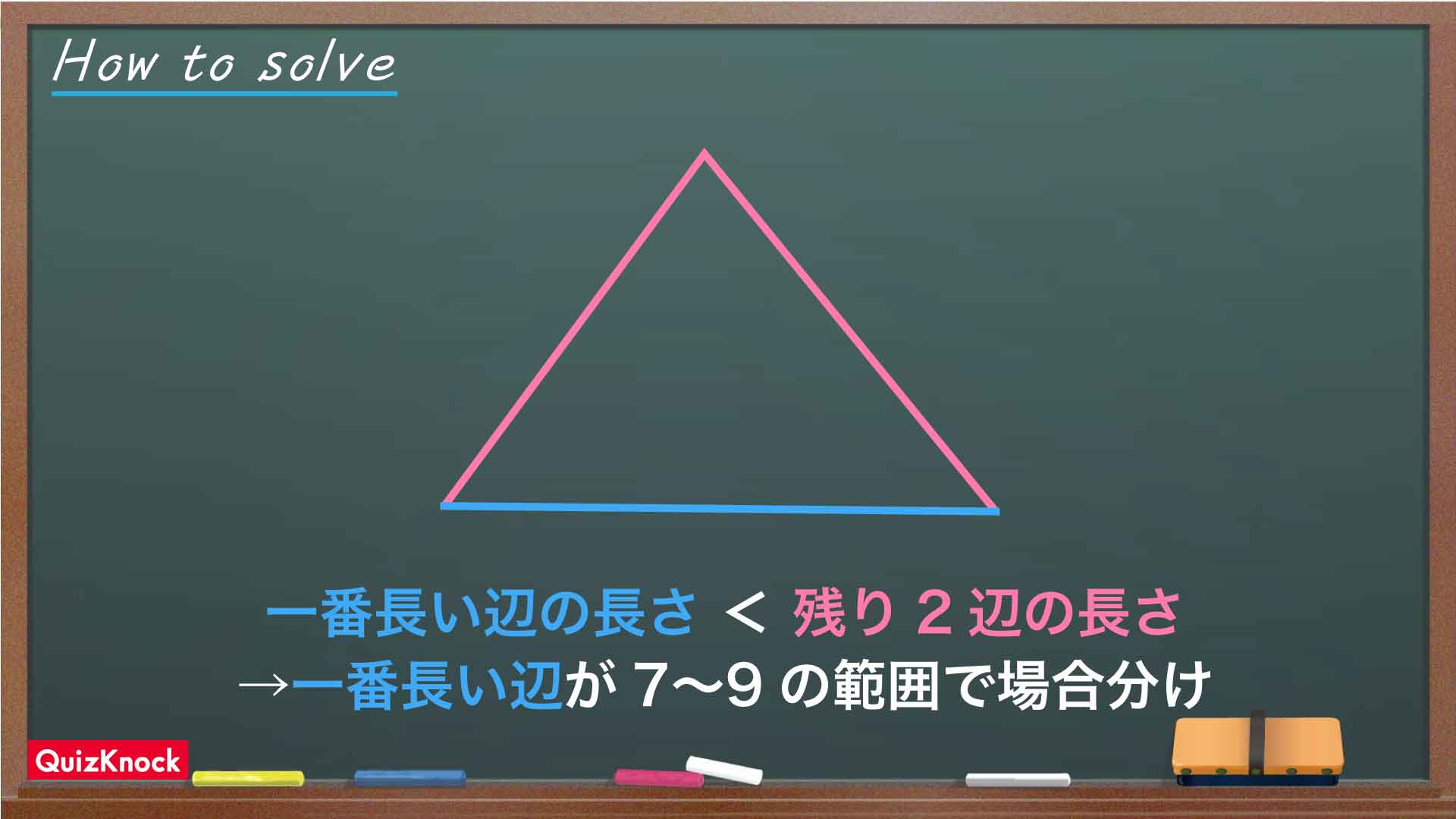
一番長い辺が満たす条件を考える
棒を折ってできる三角形の数をもれなく・ダブりなく数えるため、3辺のうちの一番長い辺に着目します。まず、一番長い辺の長さは3辺の合計を3等分した長さ以上になります。今回は3辺の長さの合計が19なので、一番長い辺の長さは19÷3=6.333……以上。問題の条件より、1辺の長さは整数なので、7以上ということになります。
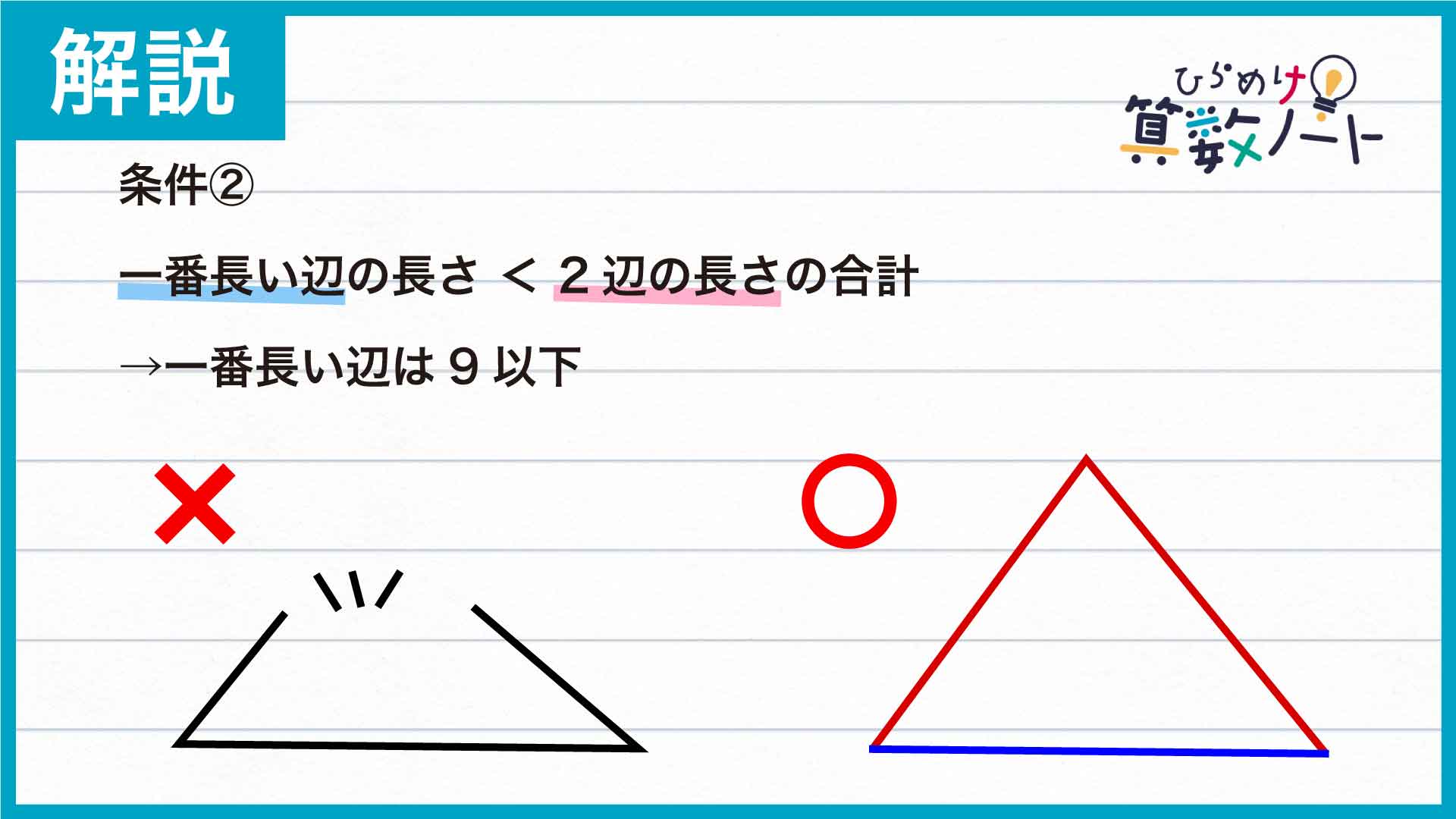
また、残り2辺の長さの合計が一番長い辺の長さ以下である場合、下の図のように三角形を作ることができません。つまり、一番長い辺の長さが残り2辺の長さの合計を下回ることがもう一つの条件です。したがって、一番長い辺の長さは19÷2=9.5未満、すなわち9以下となります。
よって、考えなければならないのは一番長い辺の長さが7、8、9のみということがわかるのです。
場合ごとに三角形を数える
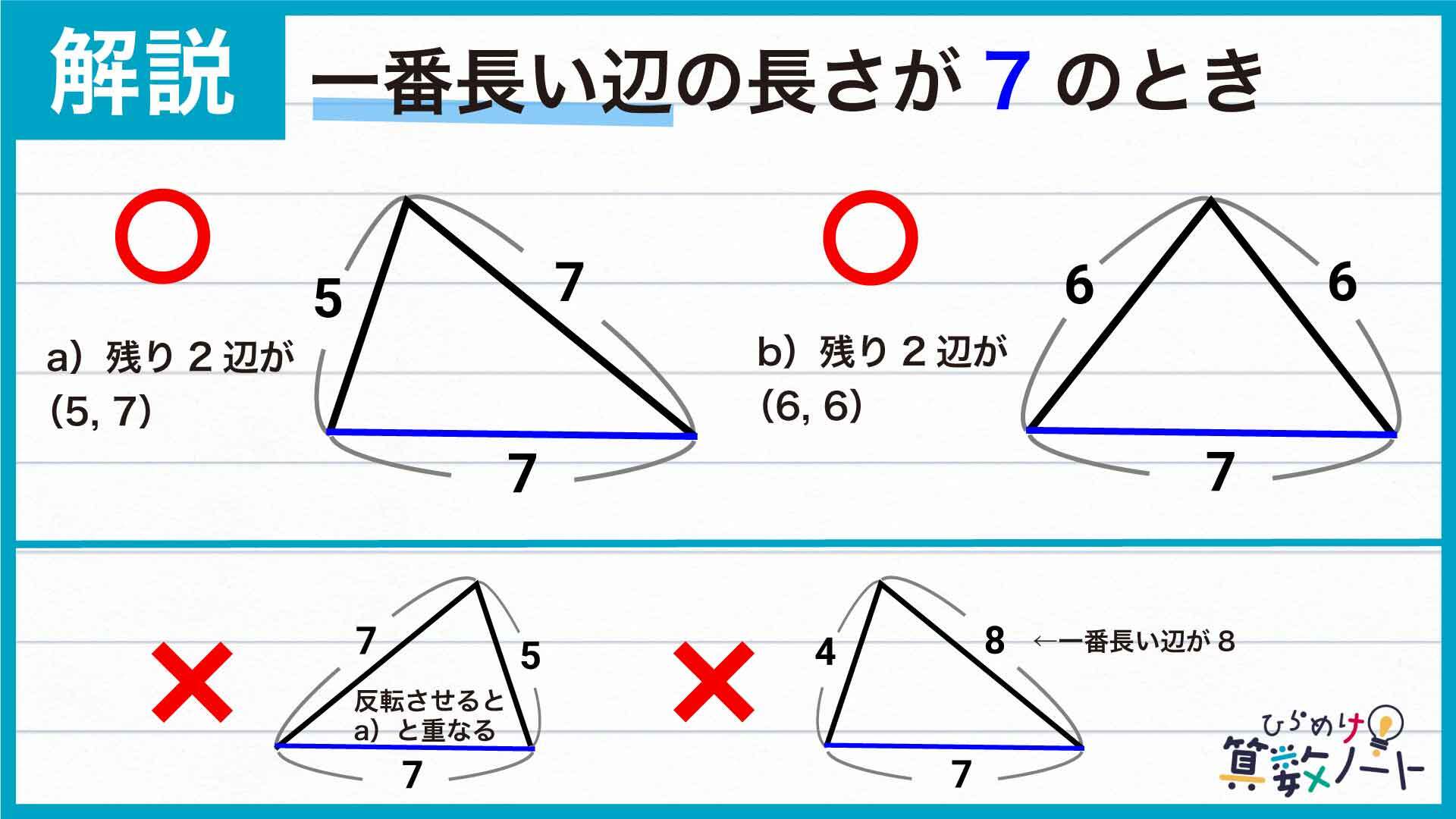
まずは、一番長い辺の長さが7である場合について考えます。このとき残り2辺の長さの合計は19-7=12であり、それぞれの辺の長さが7を超えてはいけません。このような条件を満たす2辺の長さの組み合わせは(5,7)および(6,6)の2通りのみということになります。
同様にして一番長い辺の長さが8のときの残り2辺の長さの組み合わせを考えると、(3,8)、(4,7)、(5,6)の3通り。そして一番長い辺の長さが9のとき、残り2辺の長さの組み合わせは(1,9)、(2,8)、(3,7)、(4,6)、(5,5)の5通りです。
よって、棒を折ってできる三角形は合計で2+3+5=10種類であることがわかるのです。
答え:10種類
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







