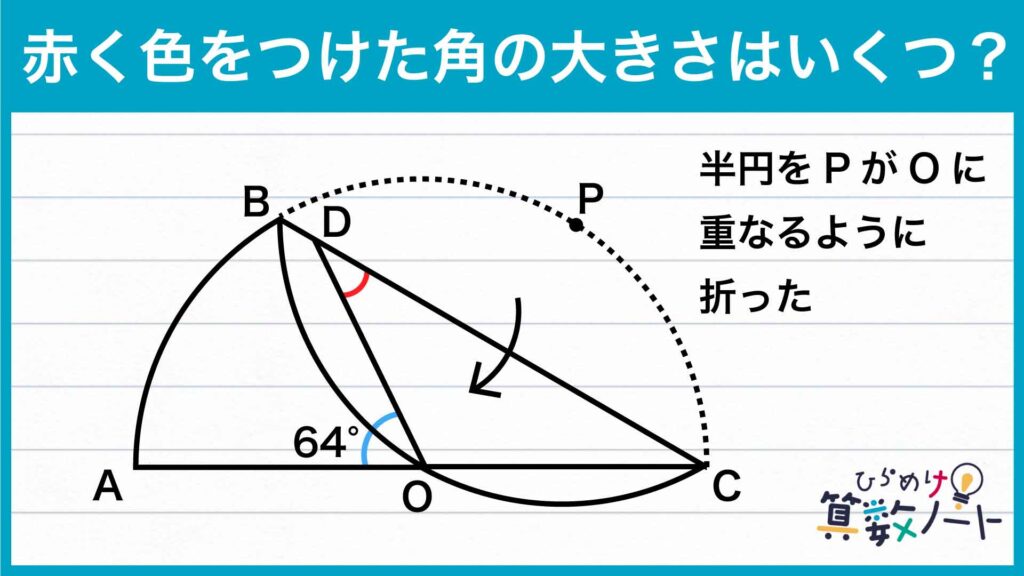
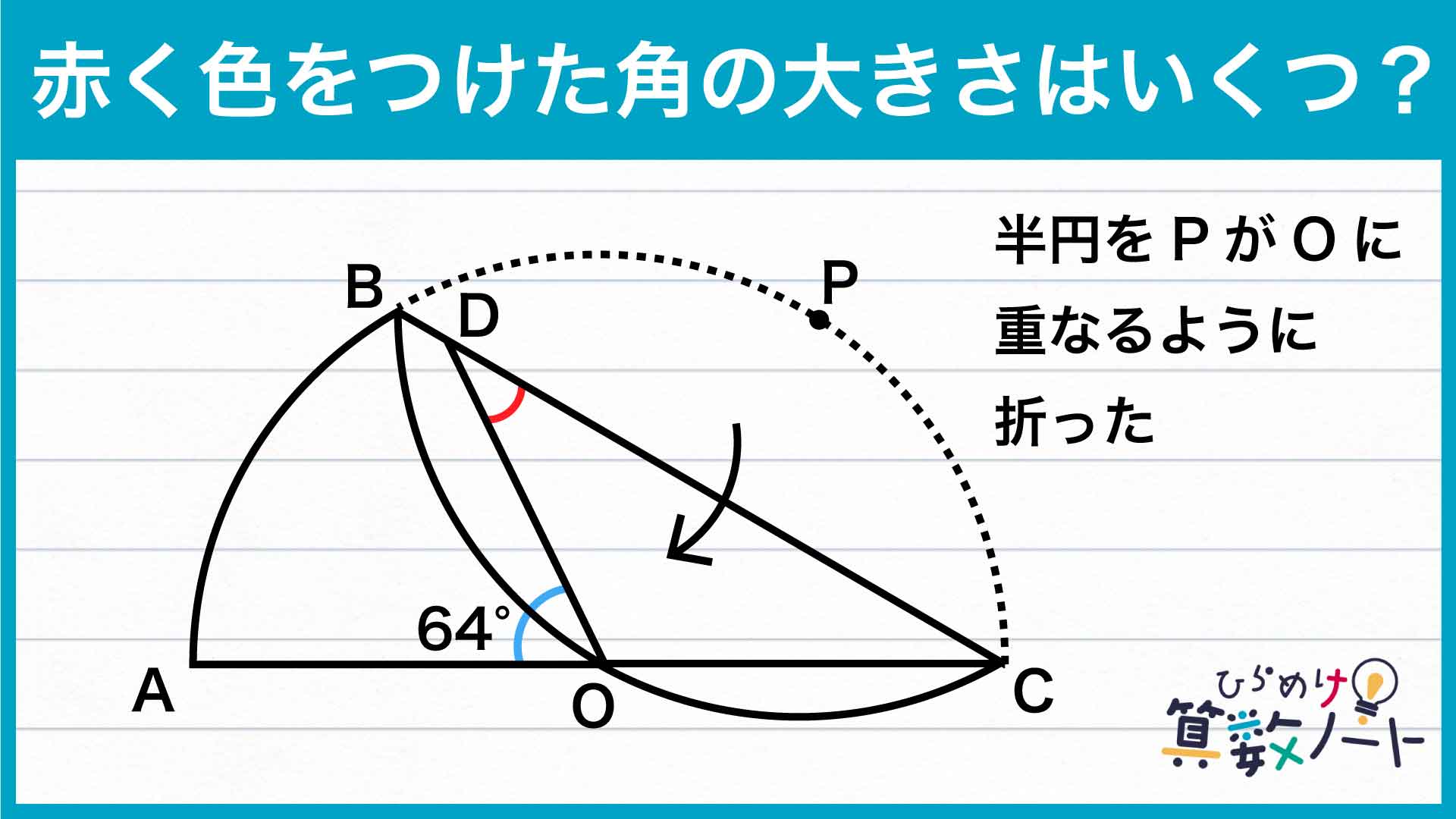
問題はこちら
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解き方をまとめた図がこちらです。
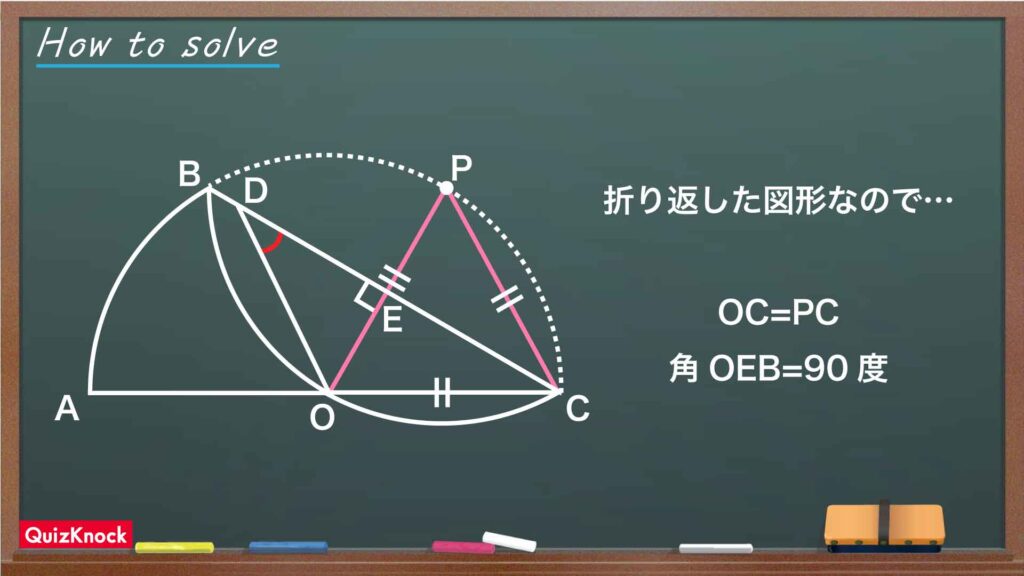
今回のポイントは、「折り返した図形の特徴をうまく利用する」ことです。
このポイントをもとに、問題を攻略していきましょう!
補助線を引く
下の図のピンク色の線のように、点Oと点P、点Cと点Pを結ぶ線を引きます。またOPとBCの交点をEとします。
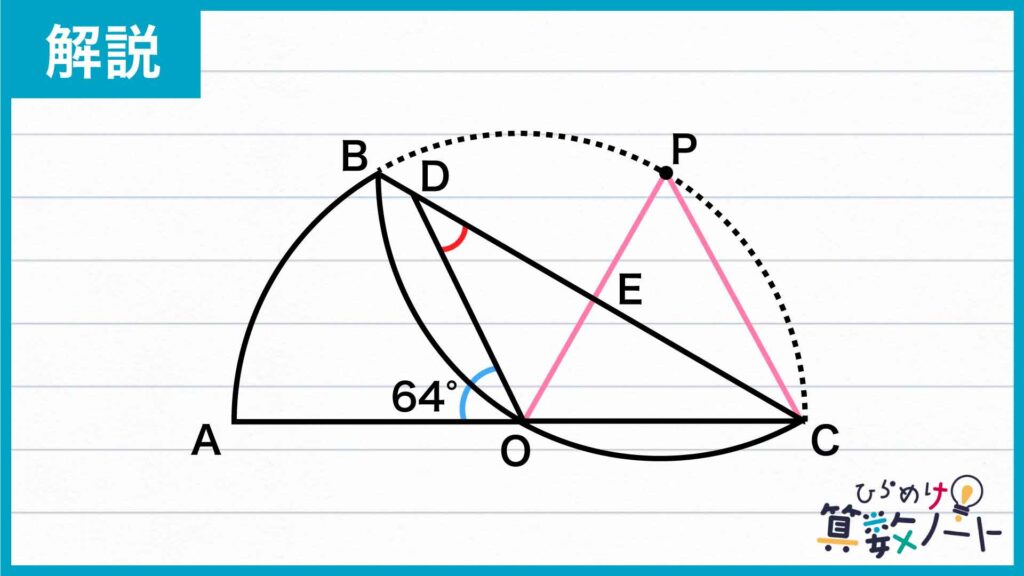
このとき、同じ半円の半径であるため、OC=OPです。また半円をPがOに重なるように折り返すとPCはOCに重なるため、OCとPCの長さは等しいことがわかります。
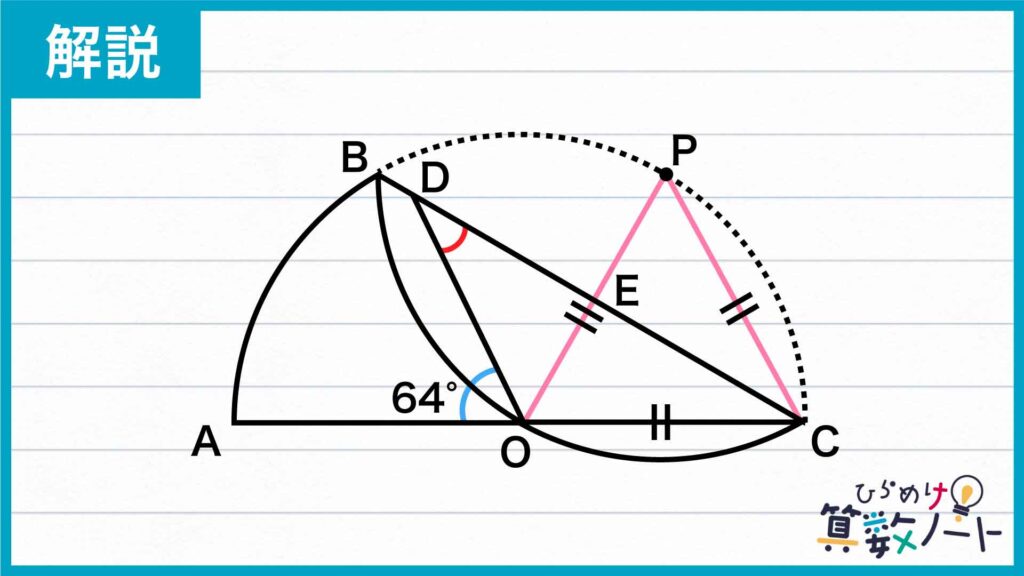
したがって、OC、OP、PCの3辺の長さが等しいので、三角形OCPは正三角形であることがわかります。
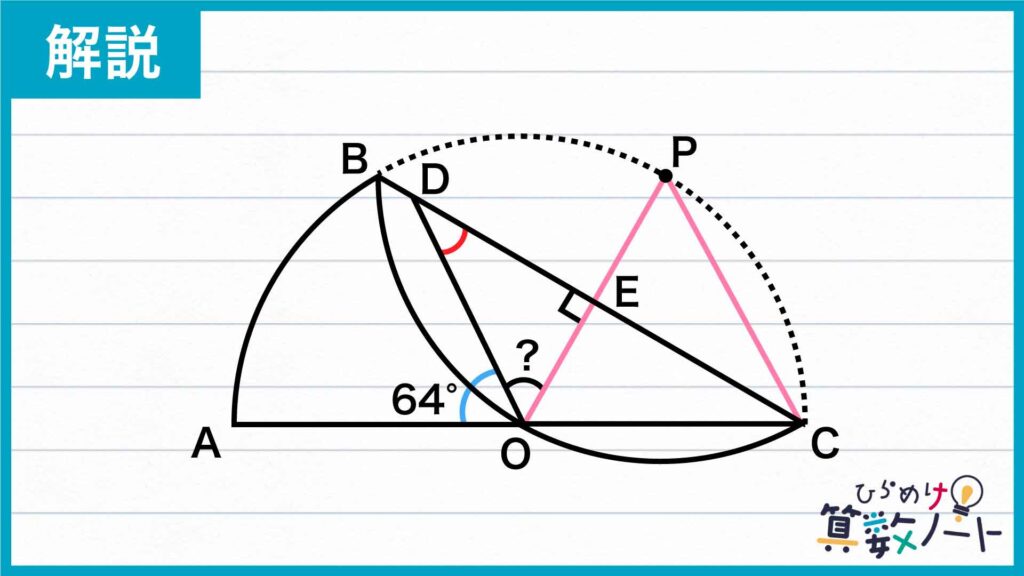
角PODの大きさを求める
半円をPがOに重なるように折り返すと、三角形PECと三角形OECはぴったりと重なります。そのため、角PECと角OECの大きさは等しくなり、180÷2=90度と求まります。したがって、角OEB=90度であることがわかります。
以上より、赤く色をつけた角の大きさは、角PODの大きさがわかれば求めることができそうです。
ここで、三角形OCPは正三角形であるため、角POC=180÷3=60度です。また角AOD=64度なので、角POD=180-64-60=56度とわかります。
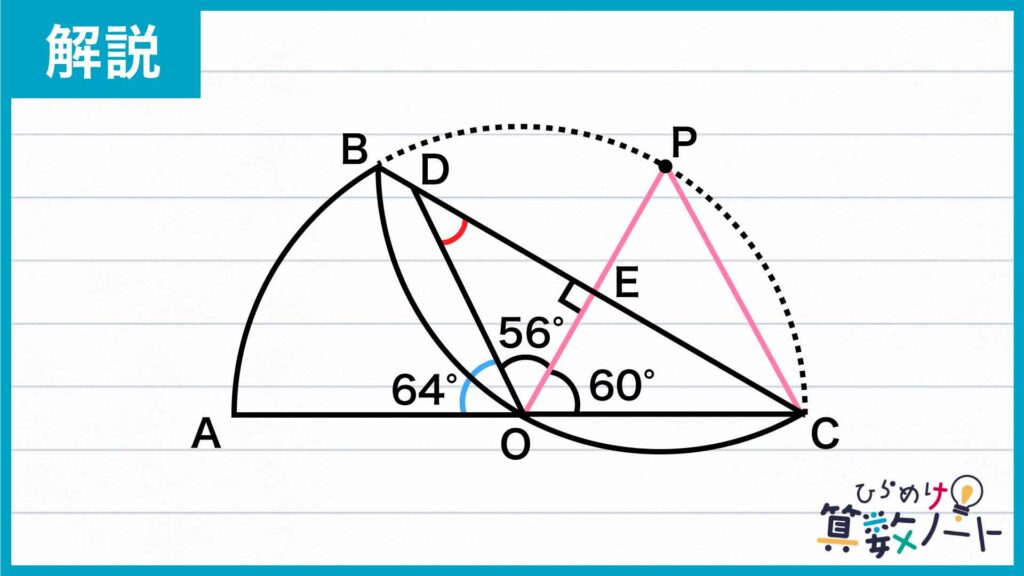
したがって、赤く色をつけた角の大きさは、180-90-56=34度となります。
答え:34度
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







