【小学生でも解ける】正五角形の紙を折る問題。あなたは解ける？

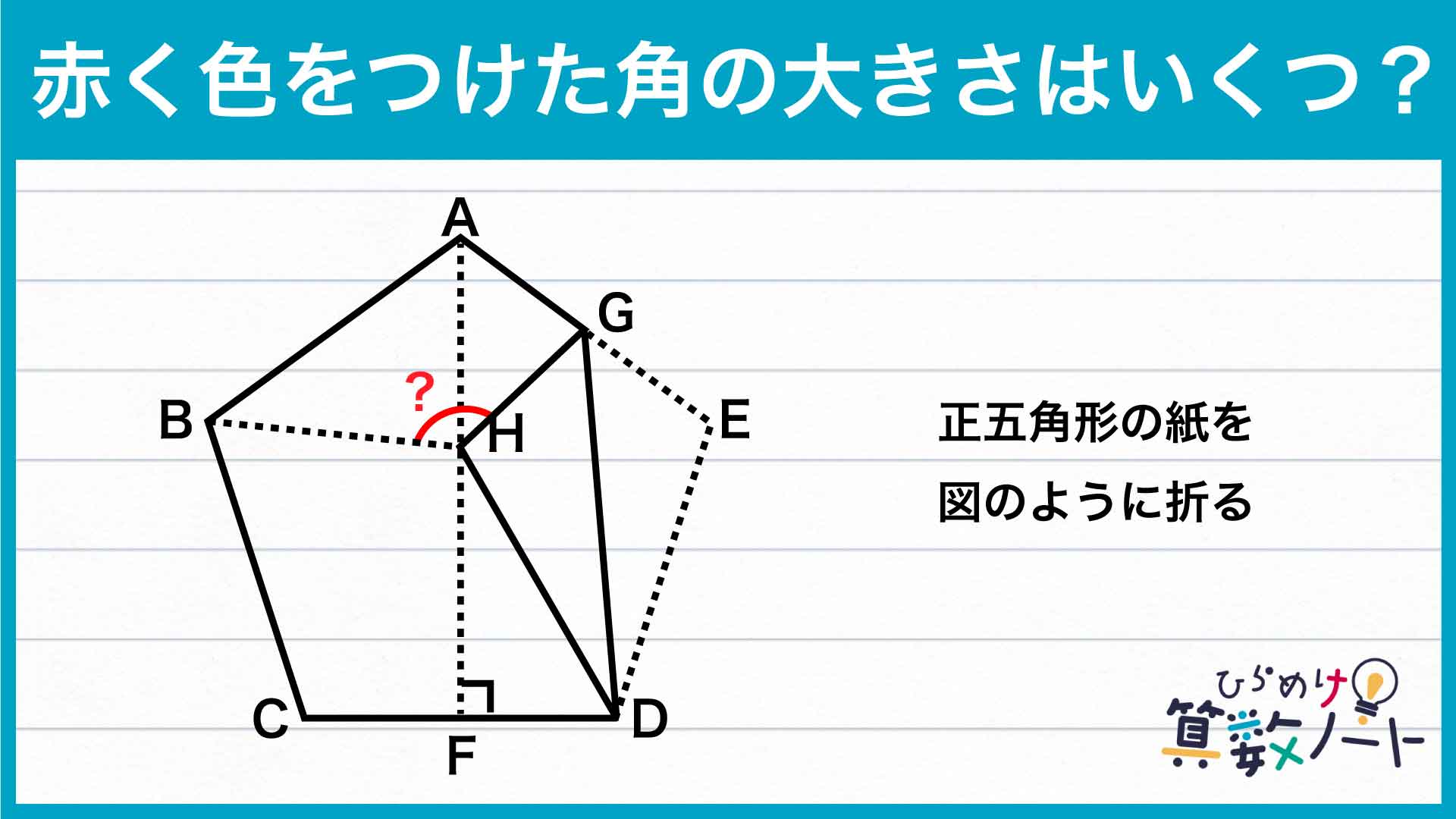
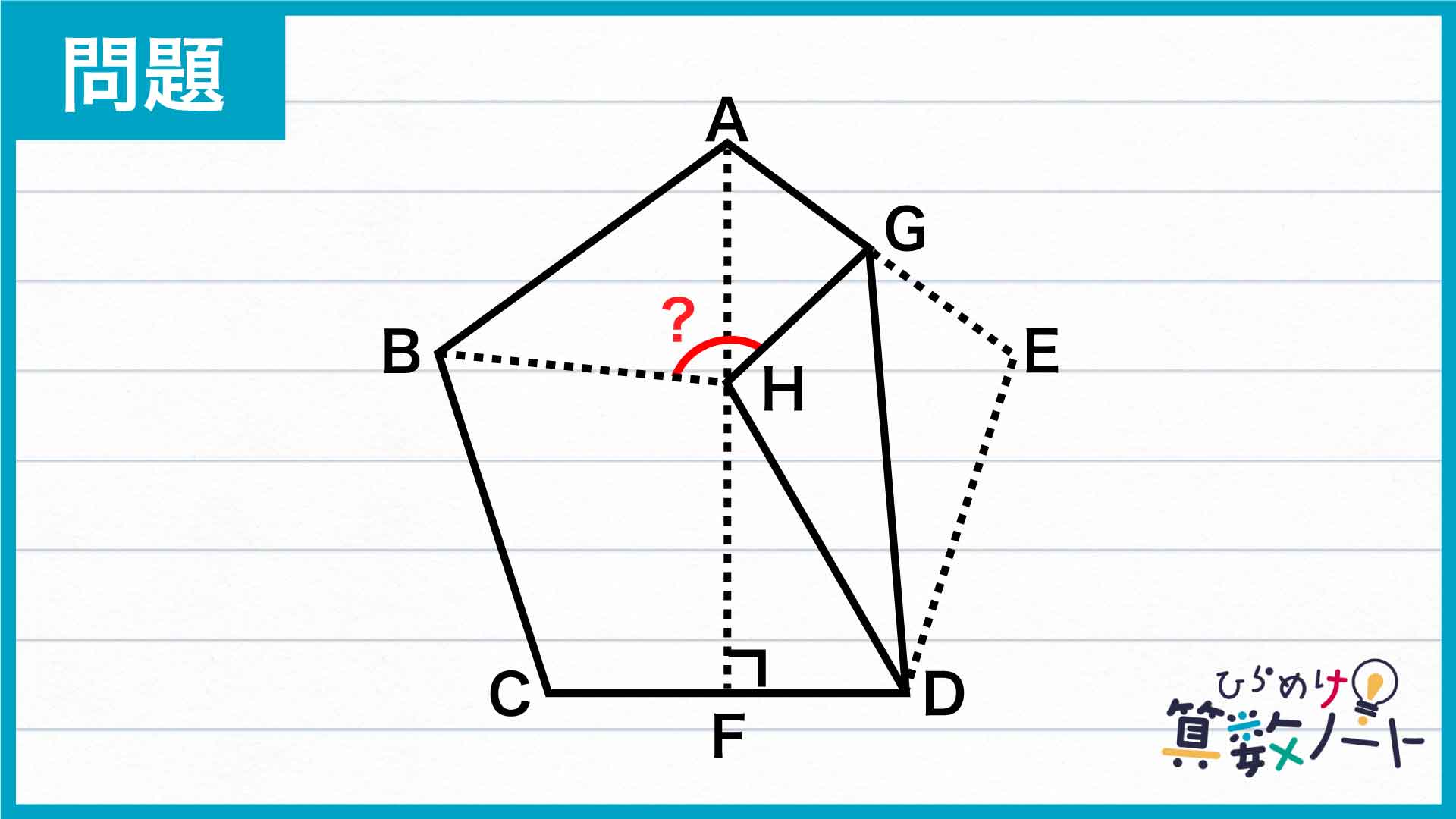
【問題はこちら】

前ページ：自力で解きたい方はこちらへ！以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題の解き方をまとめた図がこちらになります。

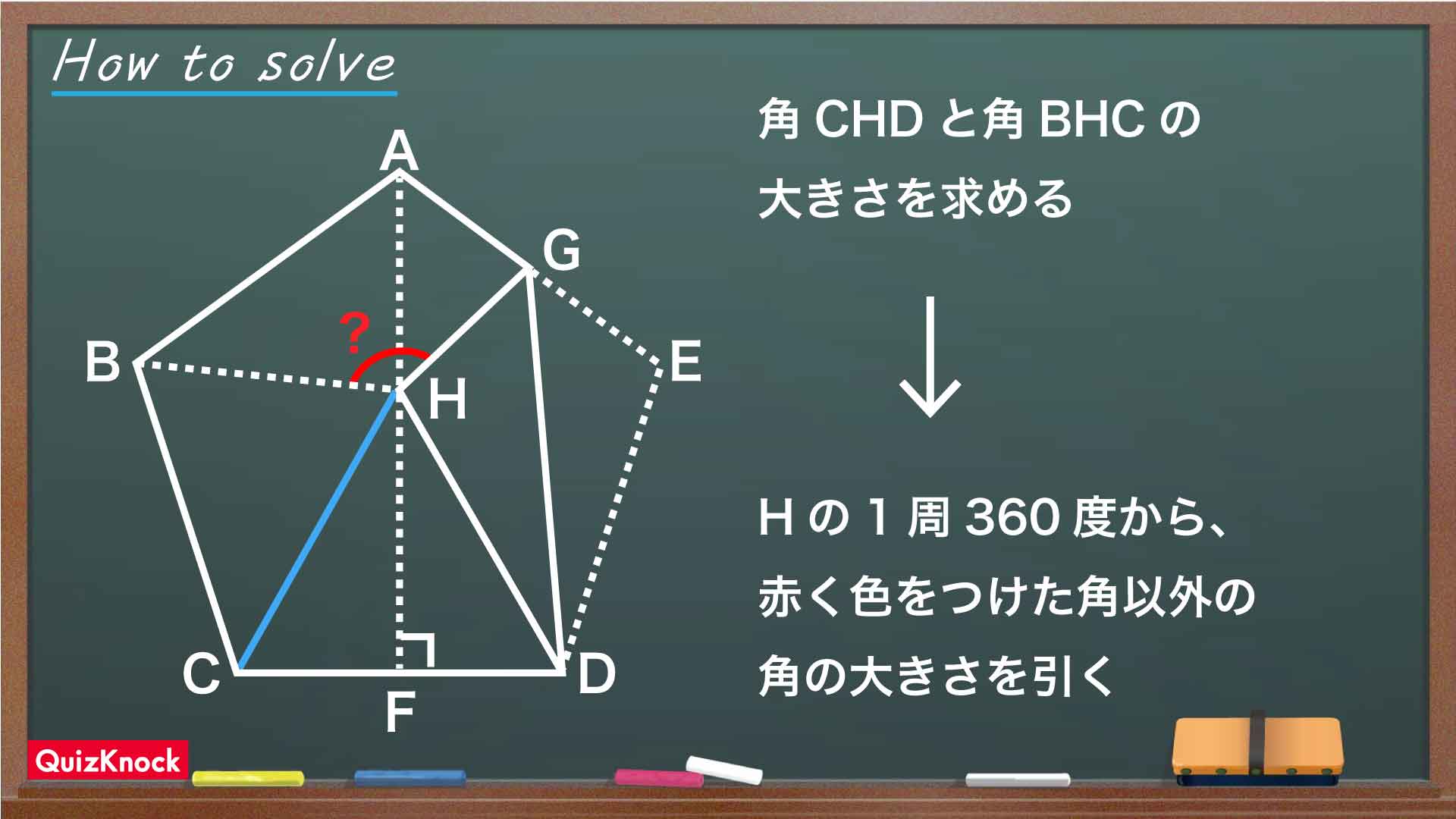
角CHDの大きさを求める

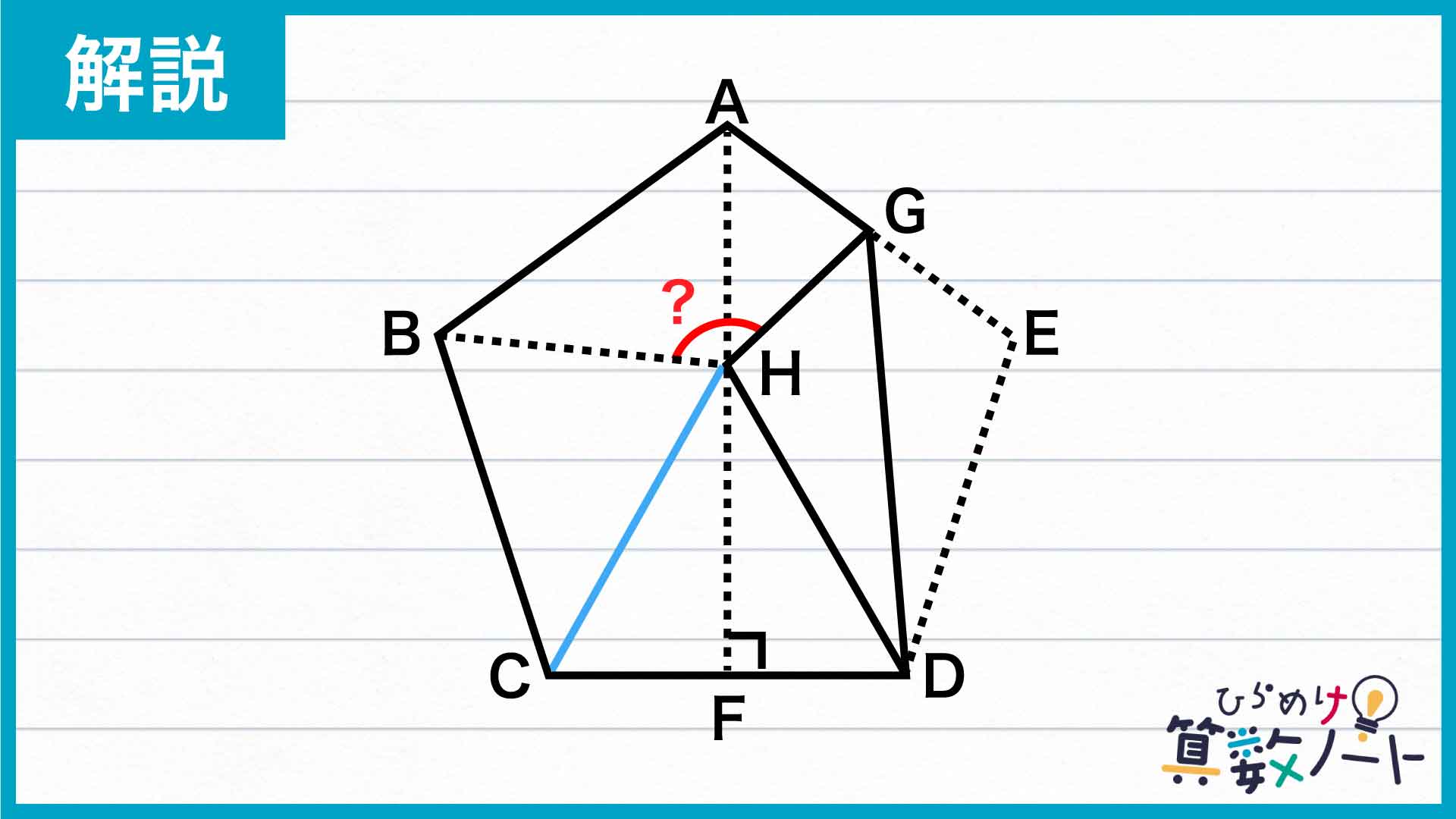
まず、下の図のように補助線を引きましょう。こうしてできた三角形HCDはどんな図形でしょうか。

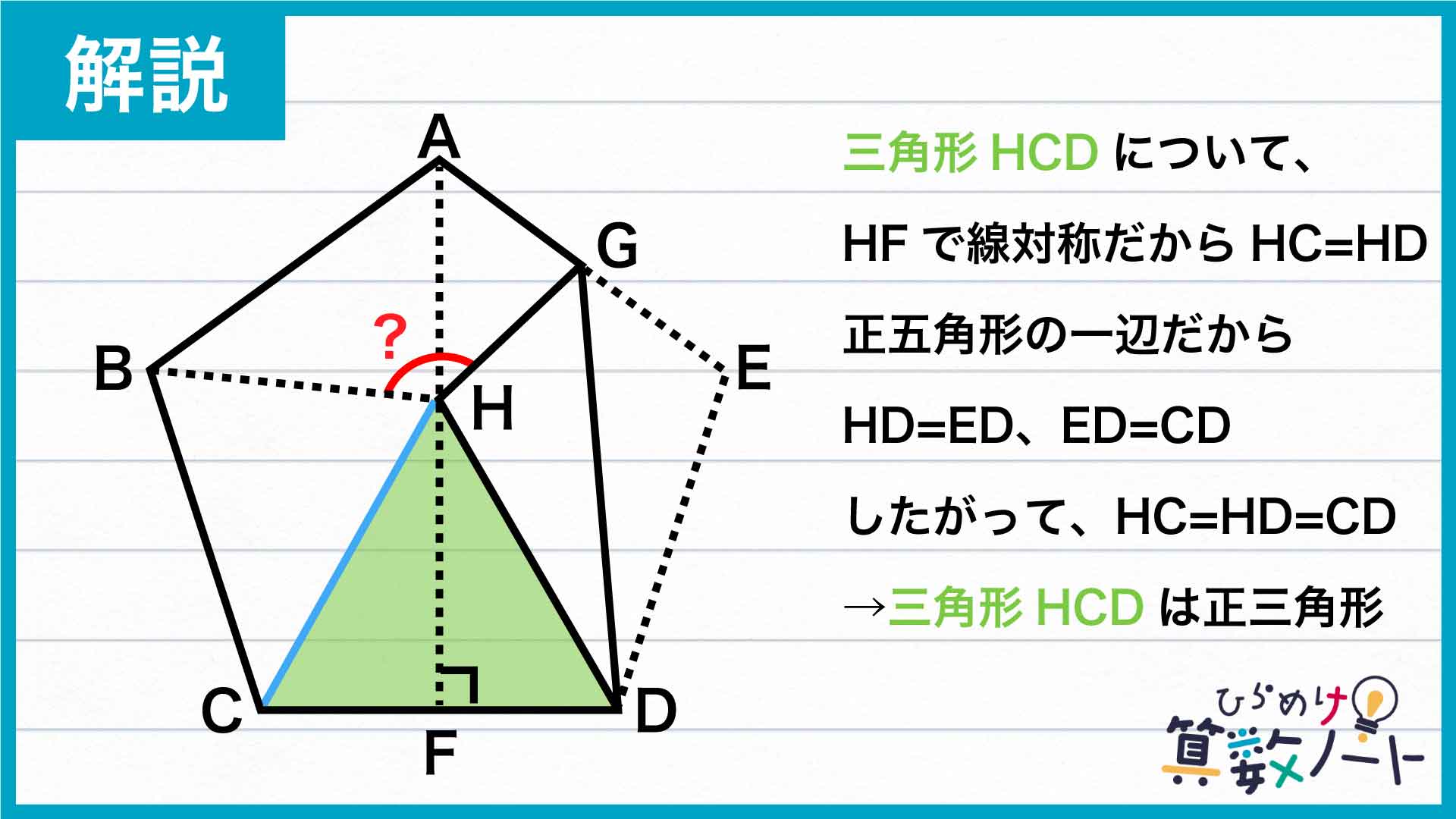
点AからCDにおろした垂線はCDを二等分し、AFは正五角形ABCDEの線対称の軸になります。点Hは対称の軸AF上の点なので、HC=HDであることがわかります。三角形HGDと三角形EGDは合同なので、HD=EDです。さらに、辺EDと辺CDはともに正五角形ABCDEの辺なので、ED=CDです。したがって、HC=HD=CDであり、三角形HCDはすべての辺の長さが等しい正三角形だとわかります。

正三角形からわかること

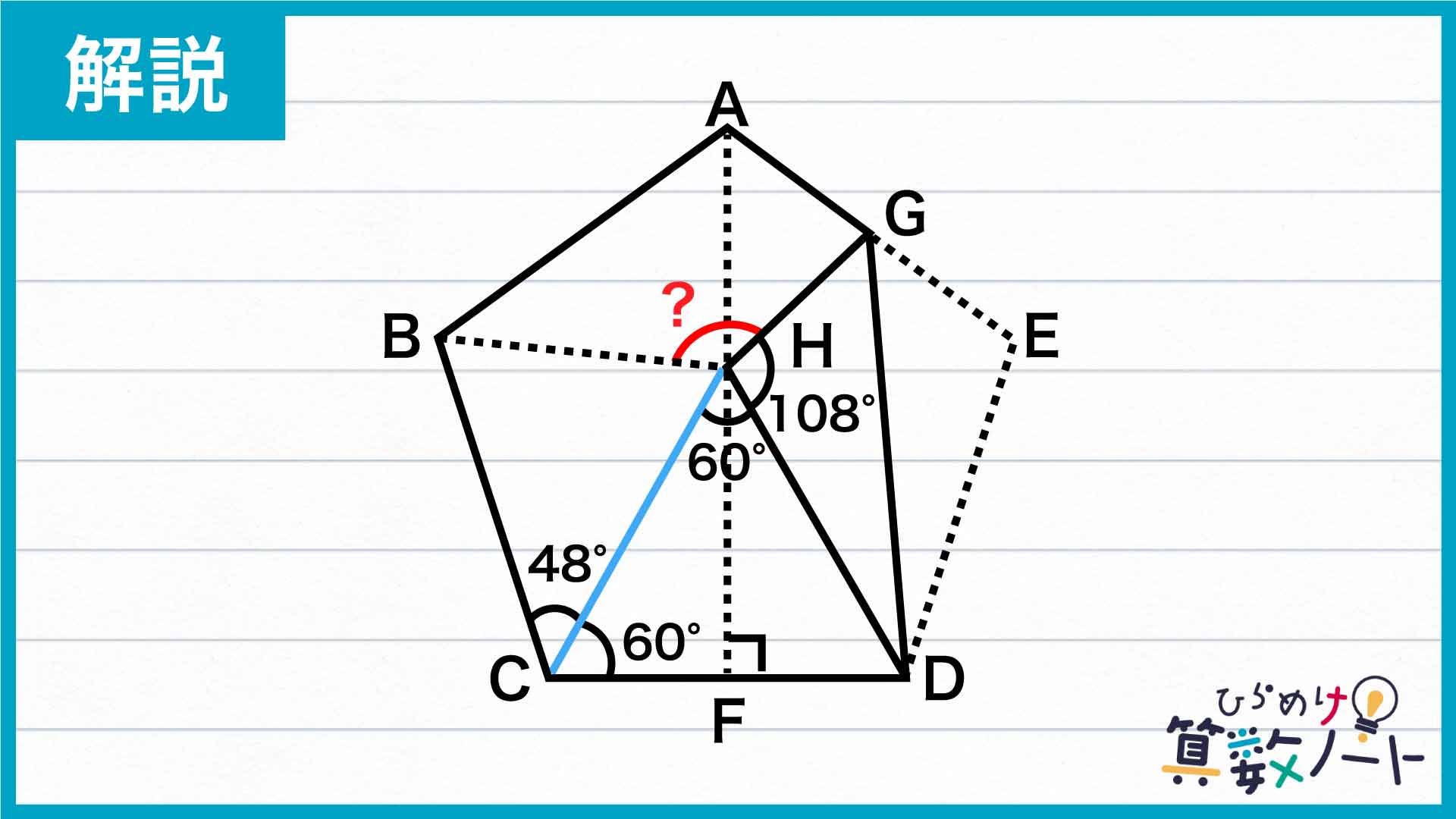
三角形HCDは正三角形だとわかったので、角HCD、角CHDの大きさは60度となります。また、正五角形の内角の和は540度なので、角GHD、角BCDの大きさは540÷5=108度です。よって、角BCHの大きさは108-60=48度となります。

角CHBの大きさを求める

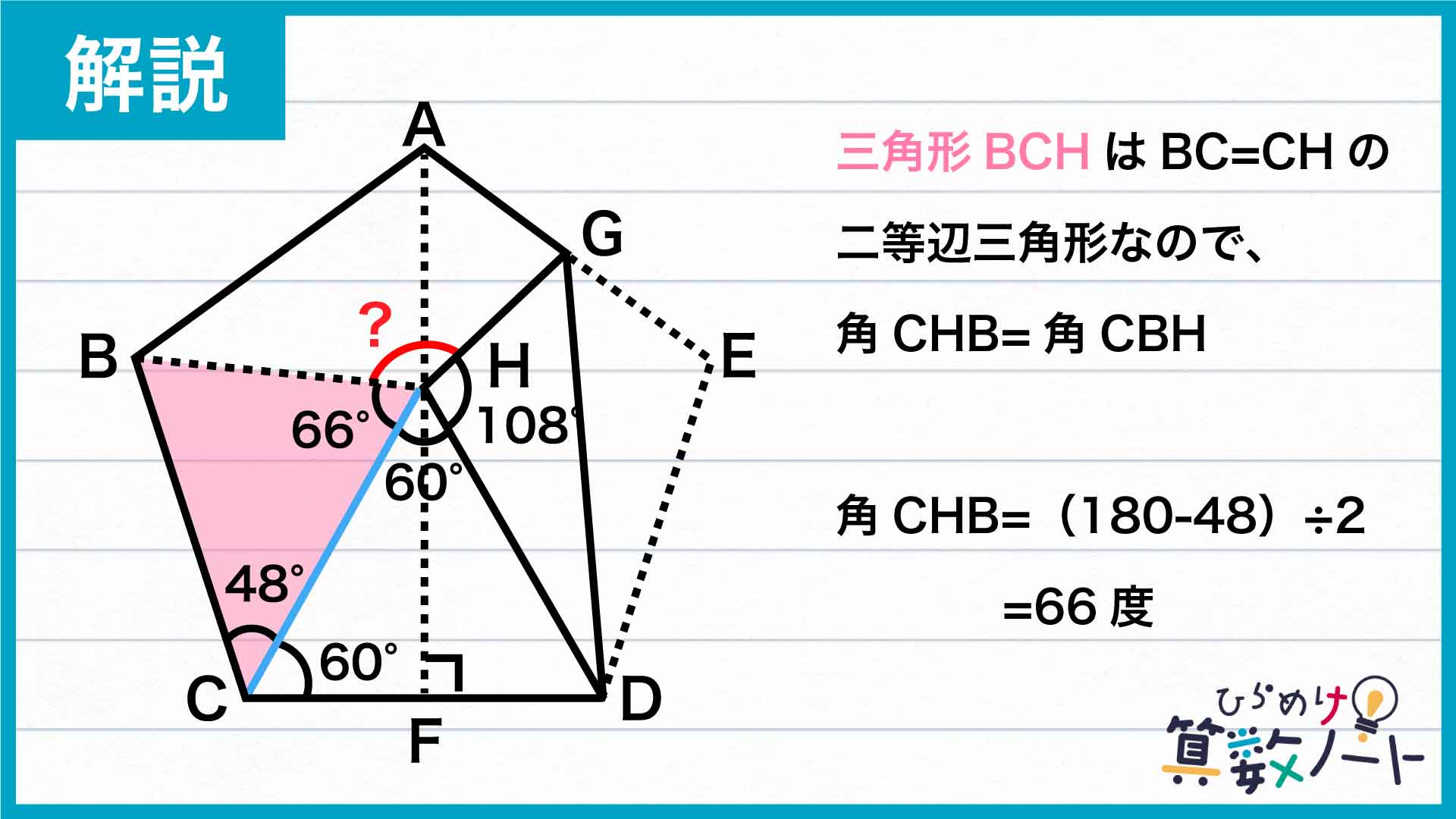
次に、三角形BCHに注目します。先ほど説明した通り、BCとCHの長さは等しいので、三角形BCHはBC=CHの二等辺三角形です。よって、角CHBと角HBCの大きさは等しく、角BCHの大きさは48度なので、角CHBの大きさは、(180-48)÷2=66度です。

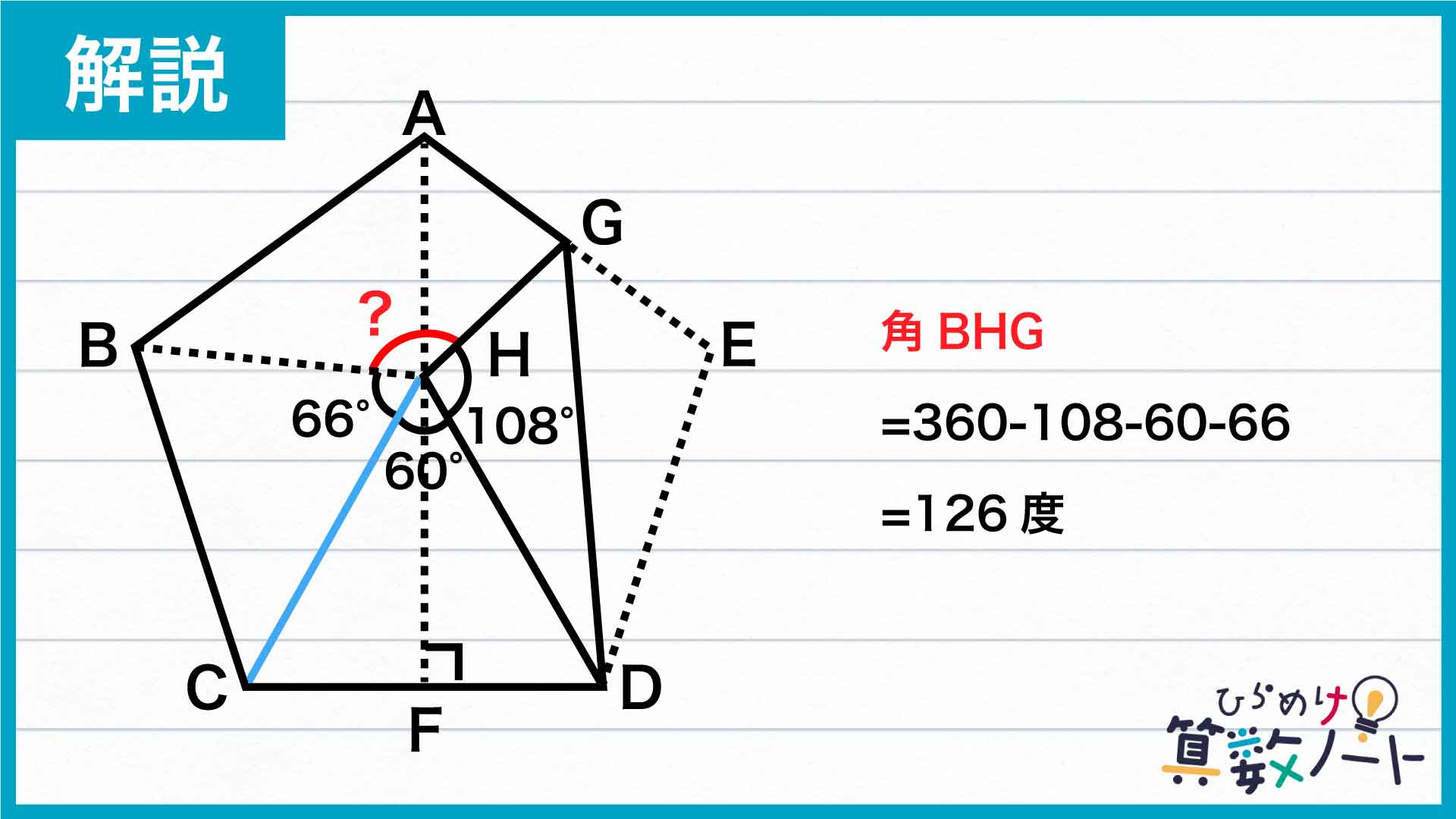
これで点Hの周りの角BHG以外の角度の大きさがすべて求まったので、角BHGの大きさは360-108-60-66=126度です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】