解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
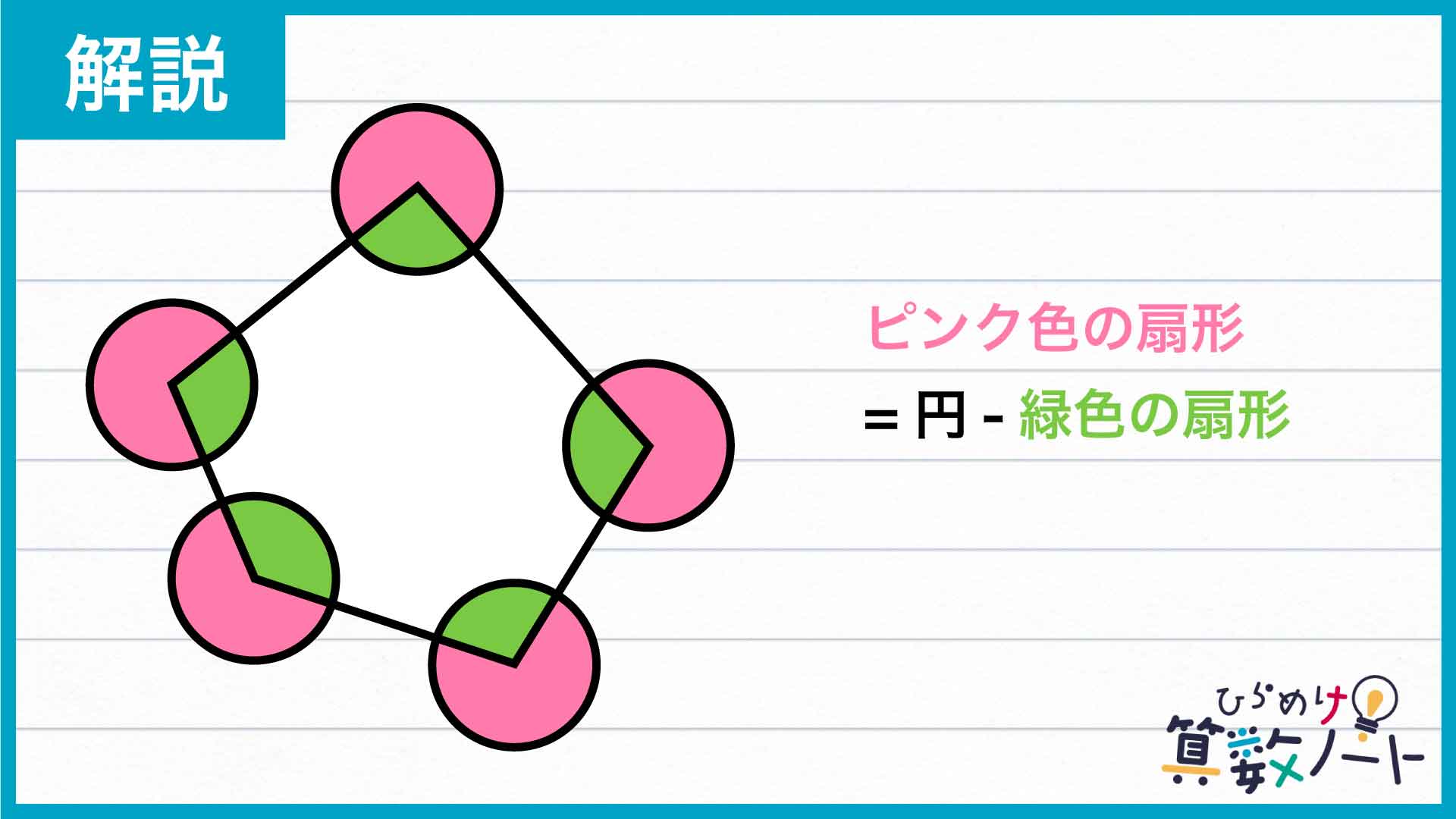
今回の解き方をまとめた図がこちらです。
今回のポイントは、「5つの扇形の面積はひとつひとつ求めるのではなく、まとめて求める」ことです。
扇形の面積は、「半径×半径×円周率(π)×(中心角の大きさ/360度)」で求めることができます。
今回、半径はすでに与えられているので、ピンク色の扇形の中心角の大きさがわかれば面積を求めることができそうです。
このポイントをもとに、問題を攻略していきましょう!
扇形の中心角の和を求める
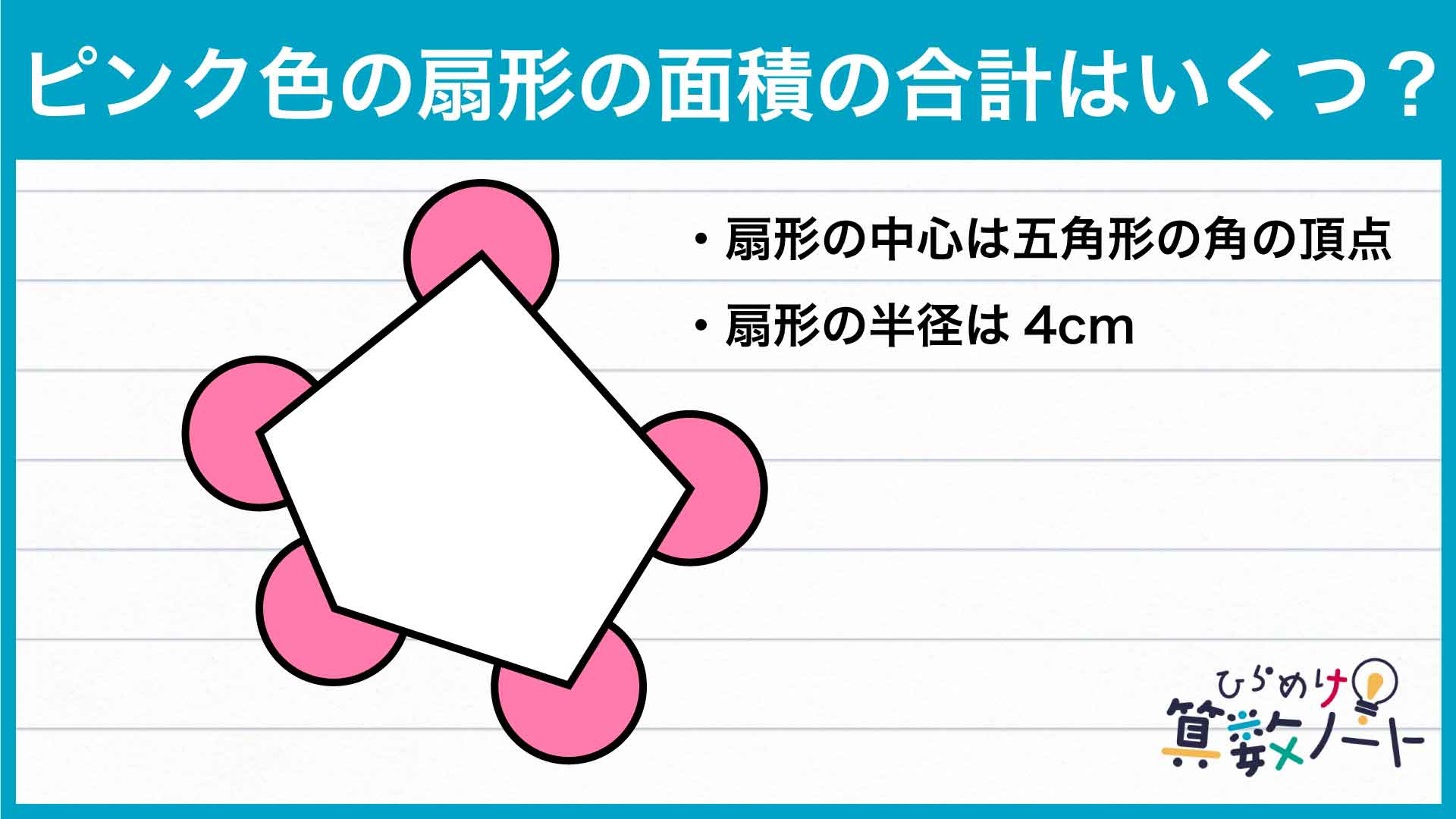
5つのピンク色の扇形は、それぞれ五角形の5つの角を中心角とする緑色の扇形を半径4cmの円から切り取ったものです。
5つの緑色の扇形の中心角の和は、五角形の内角の和と等しく540度であることから、5つのピンク色の扇形の中心角の和は、360度×5-540度=1260度と求めることができます。
扇形の合計の面積を求める
5つのピンク色の扇形の、半径と中心角の和の情報を、扇形の面積を求める公式「半径×半径×円周率(π)×(中心角の大きさ/360度)」に当てはめます。
したがって、5つのピンク色の扇形の面積の合計は、4cm×4cm×π×(1260度/360度)=56πcm2となります。
答え:56πcm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)








.jpg)






