解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解法のポイントは「三角形を作り出す」です。
正方形の一辺の長さを求めなくとも、補助線を引いて三角形を作り出すことで、正方形の面積を求めることができます。
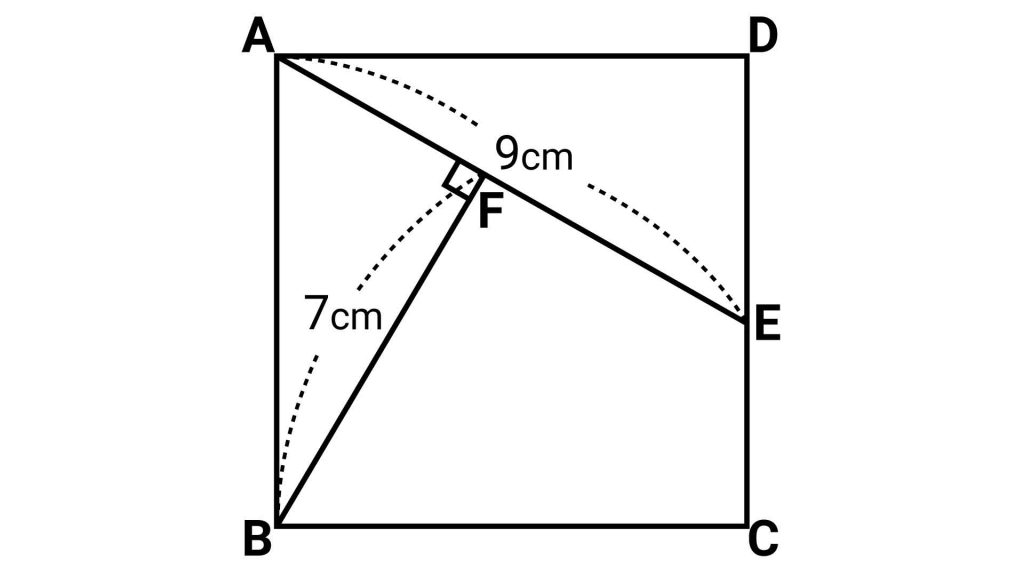
作り出す三角形は……
作り出す三角形は、三角形ABEです(BとEを結ぶ)。
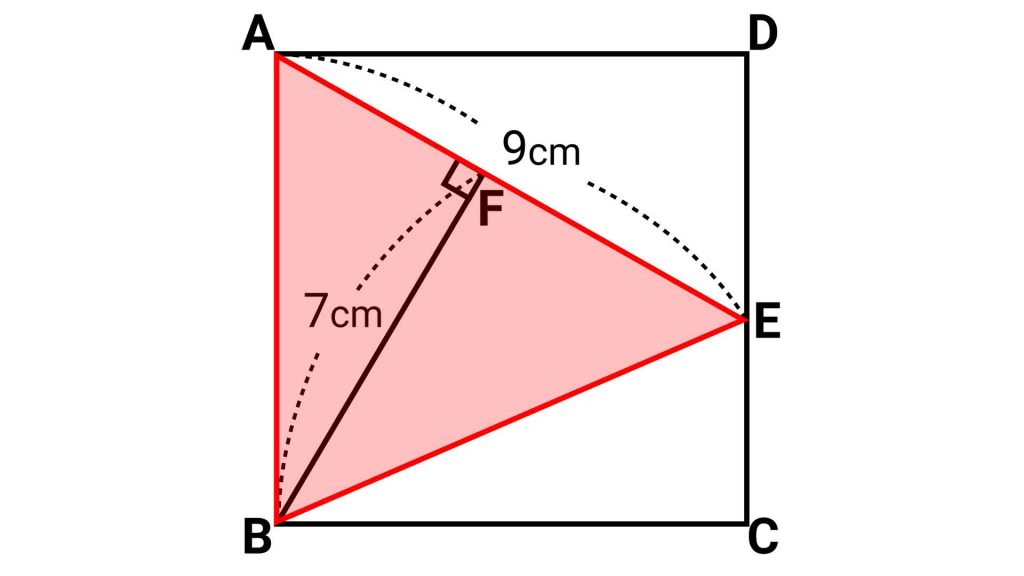
この三角形ABEの面積を使って、正方形ABCDの面積を求めることができるのです。
面積を2通りで表す
さっそく三角形ABEの面積を求めていくのですが、ここでひらめきが重要になります。以下のように、三角形ABEの面積を2通りの方法で表してみましょう。
1つ目は、長さがわかっている線分を使います。辺AEを底辺、線分BFを高さと見る方法で、(AE×BF)÷2 と表します。
2つ目は、以下の図のように、辺AB上に角AGE=90°となる点GをとってEとGを結び、辺ABを底辺、線分EGを高さと見る方法です。三角形の面積は(AB×EG)÷2 と表すことができます。
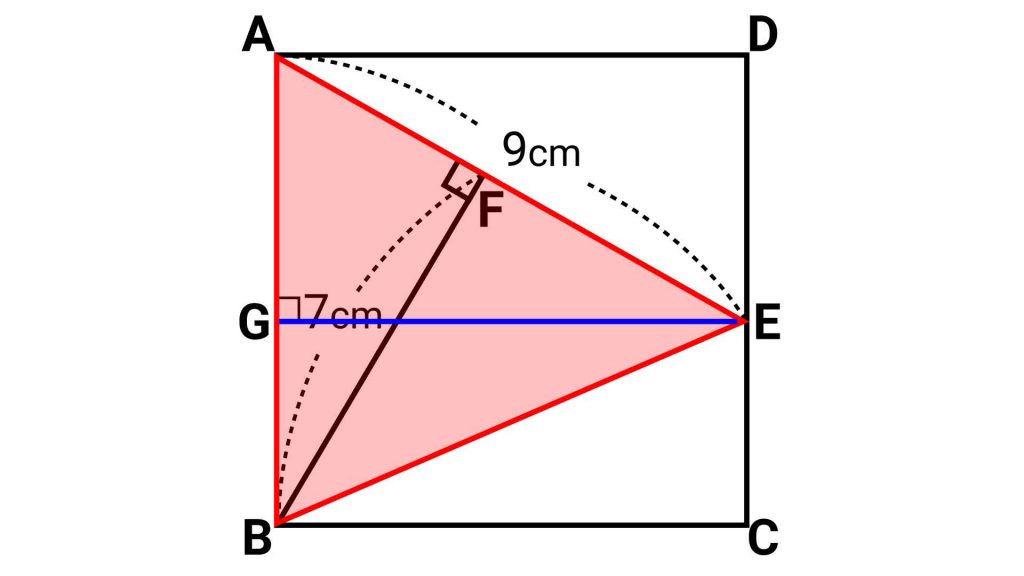
この2つの式は同じ三角形の面積を表すので、(AE×BF)÷2=(AB×EG)÷2が成り立ちます。両辺に2をかけて整理するとAE×BF=AB×EGとなります。
ここで、AB×EGについて考えます。EGはCBに平行であることからEG=CBであるため、AB×EG=AB×CBとなります。ABもCBも正方形ABCDの一辺であるため、AB×CBはそのまま正方形ABCDの面積を表します。
したがって、AB×CB、AB×EG、AE×BFはすべて正方形ABCDの面積を表します。AE=9cm、BF=7cmであることから、正方形ABCDの面積は、AE×BF=9×7=63cm2と求めることができるのです。
答え:63cm2
補助線で魔法のように解けてしまう、面積の問題でした。
それでは。
【あわせて読みたい】









.jpg)









.jpg)







