解説
それでは解説です。立体的にイメージしながら地道に数える方法でも答えにはたどり着けますが、ここではもっと簡単で間違えにくい解法を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
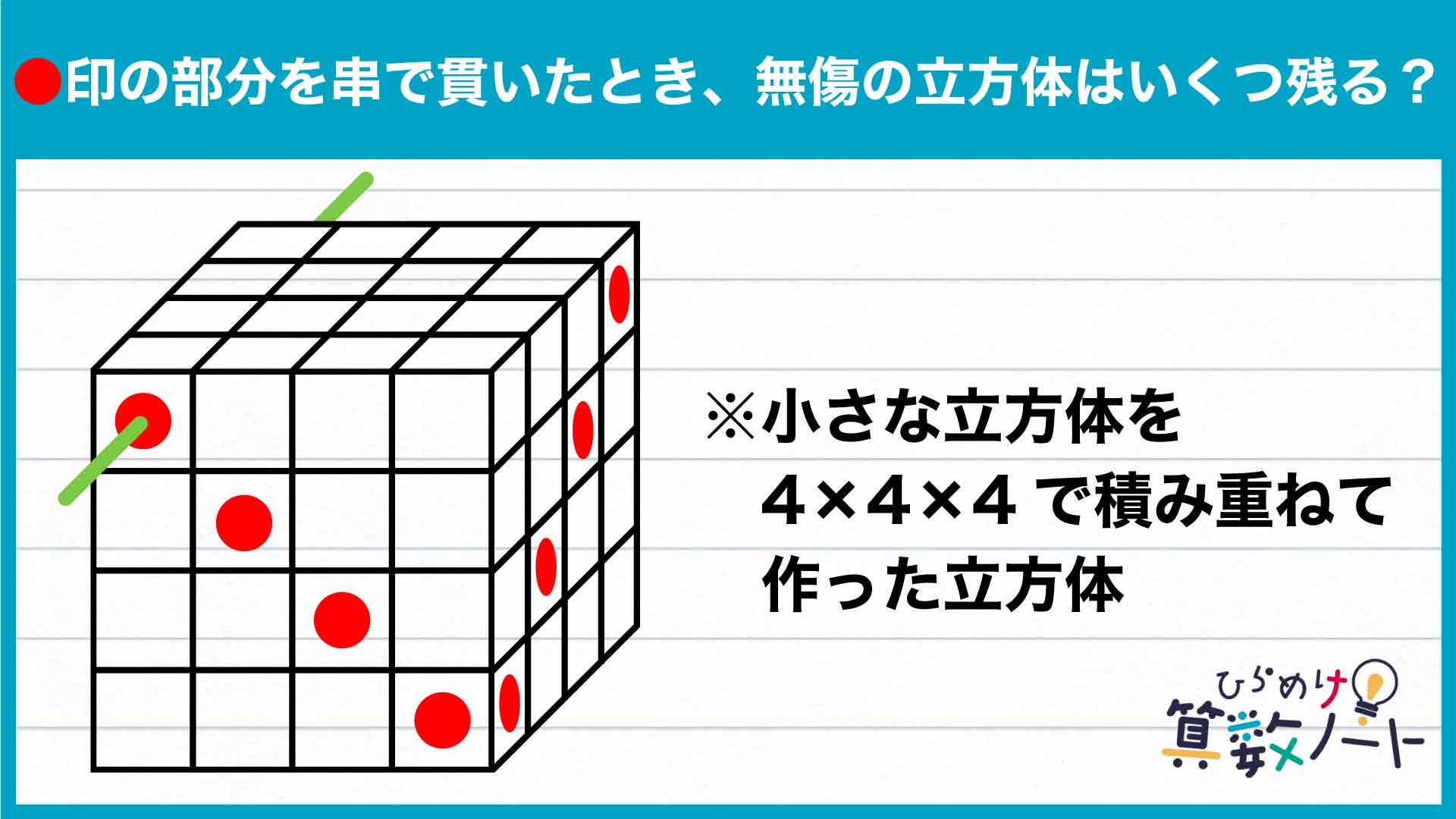
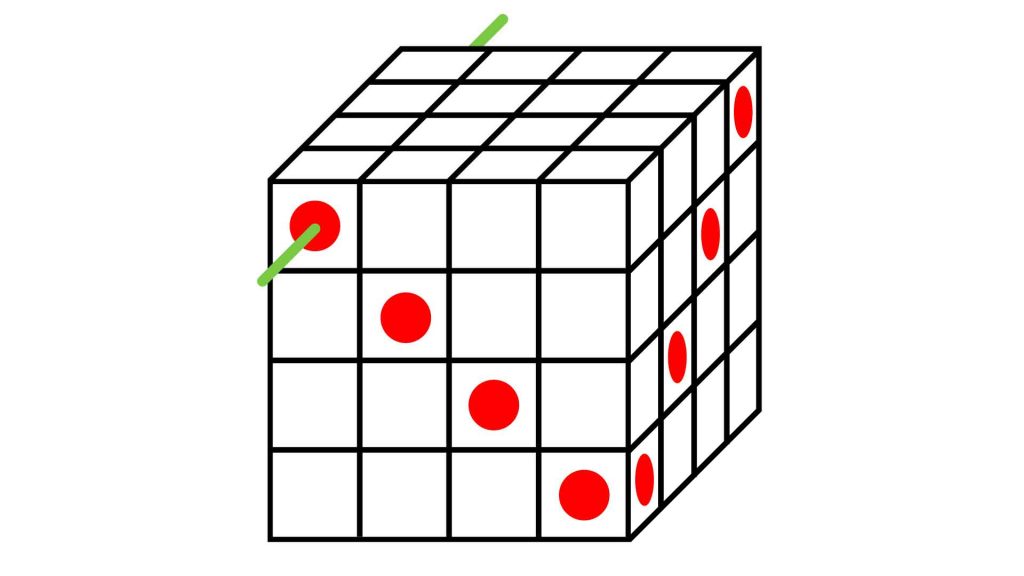
今回は私と一緒に解いていきましょう! 見えない串や立方体を想像するのは難しいですよね。うまく数えるにはどうしたらいいのでしょうか?
今回のポイントは、「1段ずつ分けて考える」ことです。
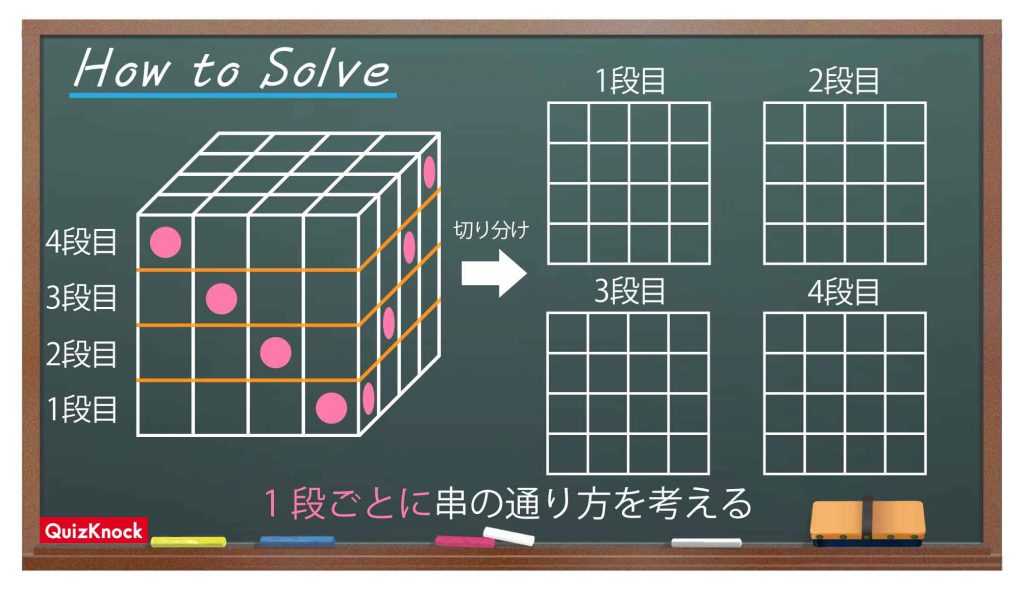
大きな立方体を4つの段に分けるだけで、無傷の立方体が一気に数えやすくなります。
上のように切り分けることで、4個×4個の段が4つできます。これにより、外側から見えない立方体もイメージしやすくなりました。
あとは、1段ずつ串の通り方を検討していけば、答えにたどり着けます。
1段ごとに無傷の立方体を数える
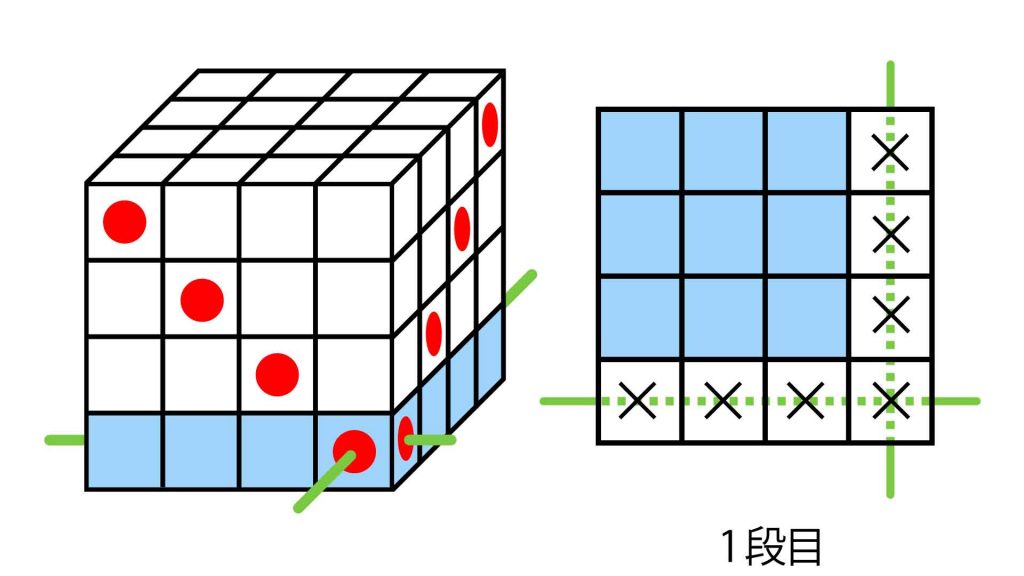
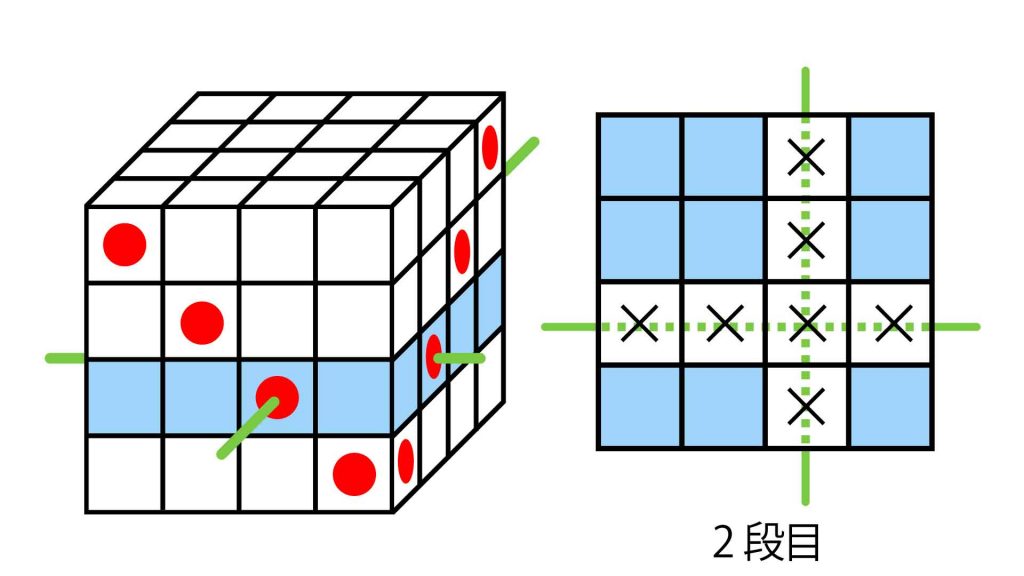
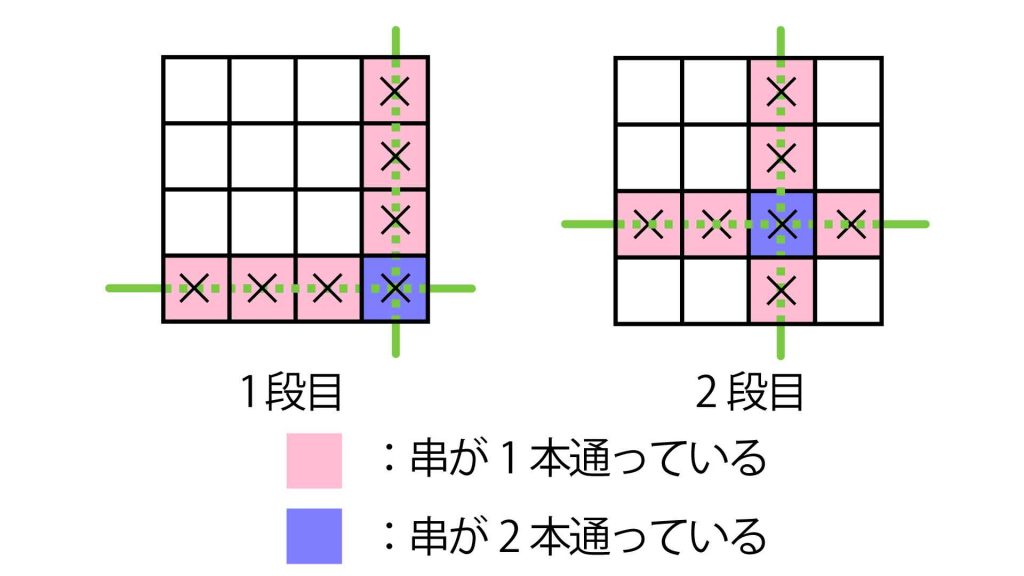
一番下の段を上から見ると、次の図のように串が通っています。無傷の立方体が9個あるのがわかりますね。
次に、下から2段目を同じように見てみると、この段も9個だけ無傷で残っています。
刺さり方の法則を見つける
ここで、勘の良い方はあることに気づいたかと思います。1段目と2段目で無傷の立方体の数が同じなのは、実は偶然ではないのです。
今回使われている串は全て、1本につき4つの立方体を串刺しにしています。そして、串は各段に2本ずつ刺さっており、どこかで必ず交差しています。つまり、各段に1個ずつ、2本の串に貫かれた立方体が存在しているのです。
それぞれの串が4個ずつ立方体を貫き、そのうち1個だけ重複して貫いているので、各段で4×2-1=7個の立方体が串刺しにされます。1段には16個の立方体があるので、各段で4×4-7=9個の立方体が無傷で残るのです。
以上より、無傷の立方体の合計は、9(個)× 4(段)=36個となります。
答え:36個
段ごとに分けて考えられるかがポイントになる問題でした。
またの挑戦をお待ちしています!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)








.jpg)






