解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
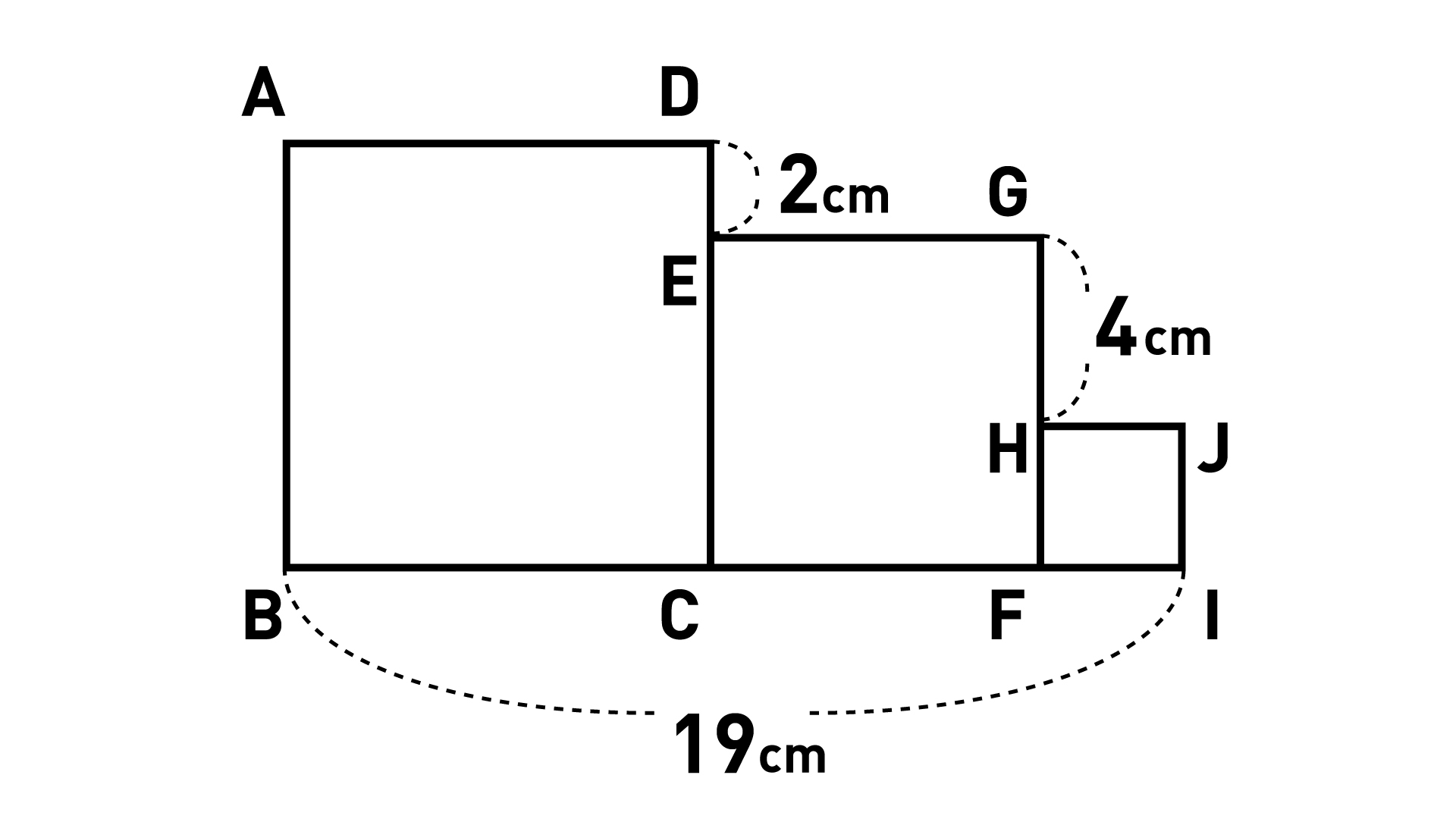
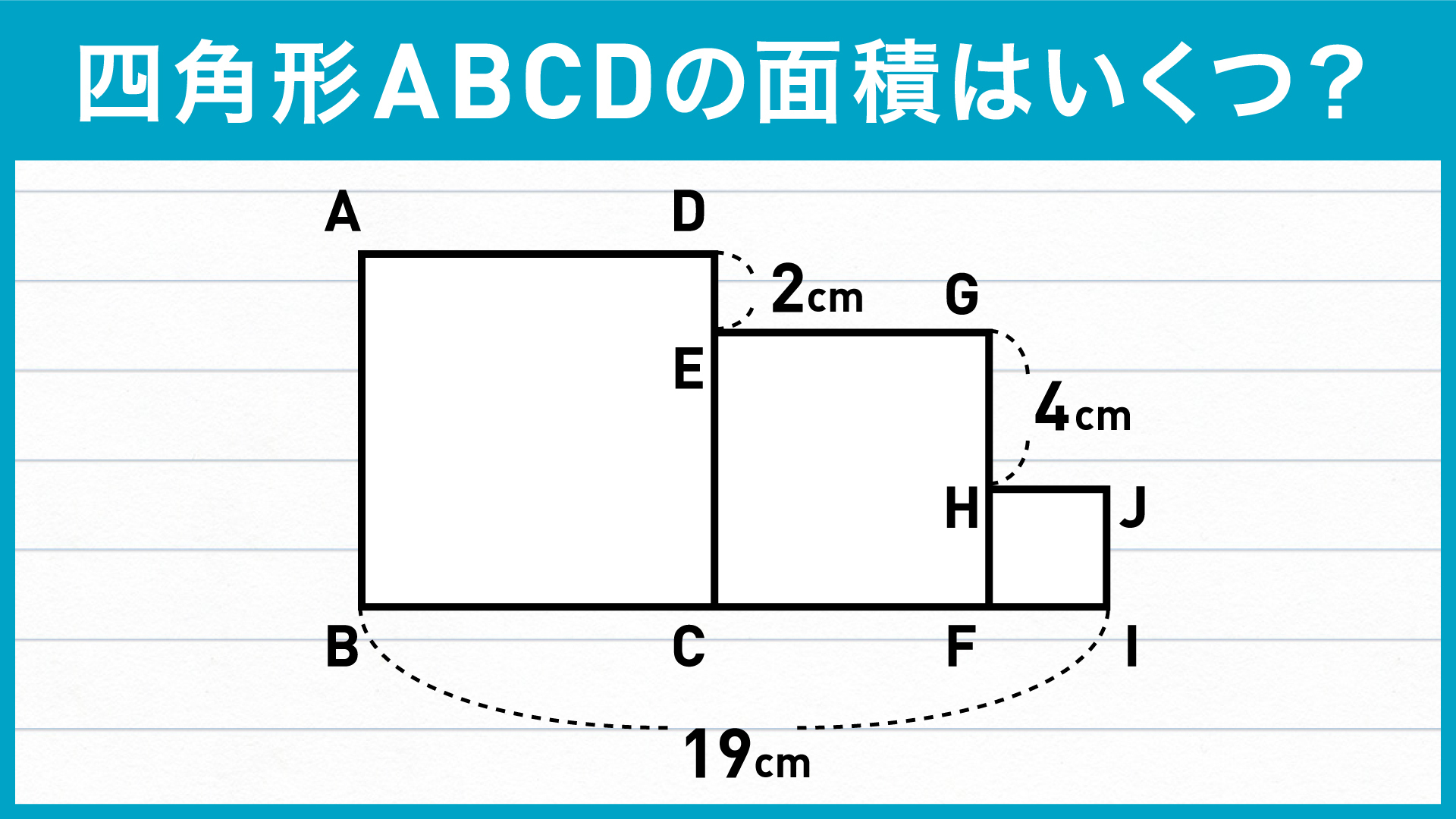
大きい正方形(正方形ABCD)の面積を求めるには、正方形ABCDの一辺の長さを知る必要があります。
そのヒントとなるのが、真ん中にある正方形ECFGの一辺の長さです。これに線分DEの長さ2cmを足すことで、正方形ABCDの一辺の長さを求めることができます。
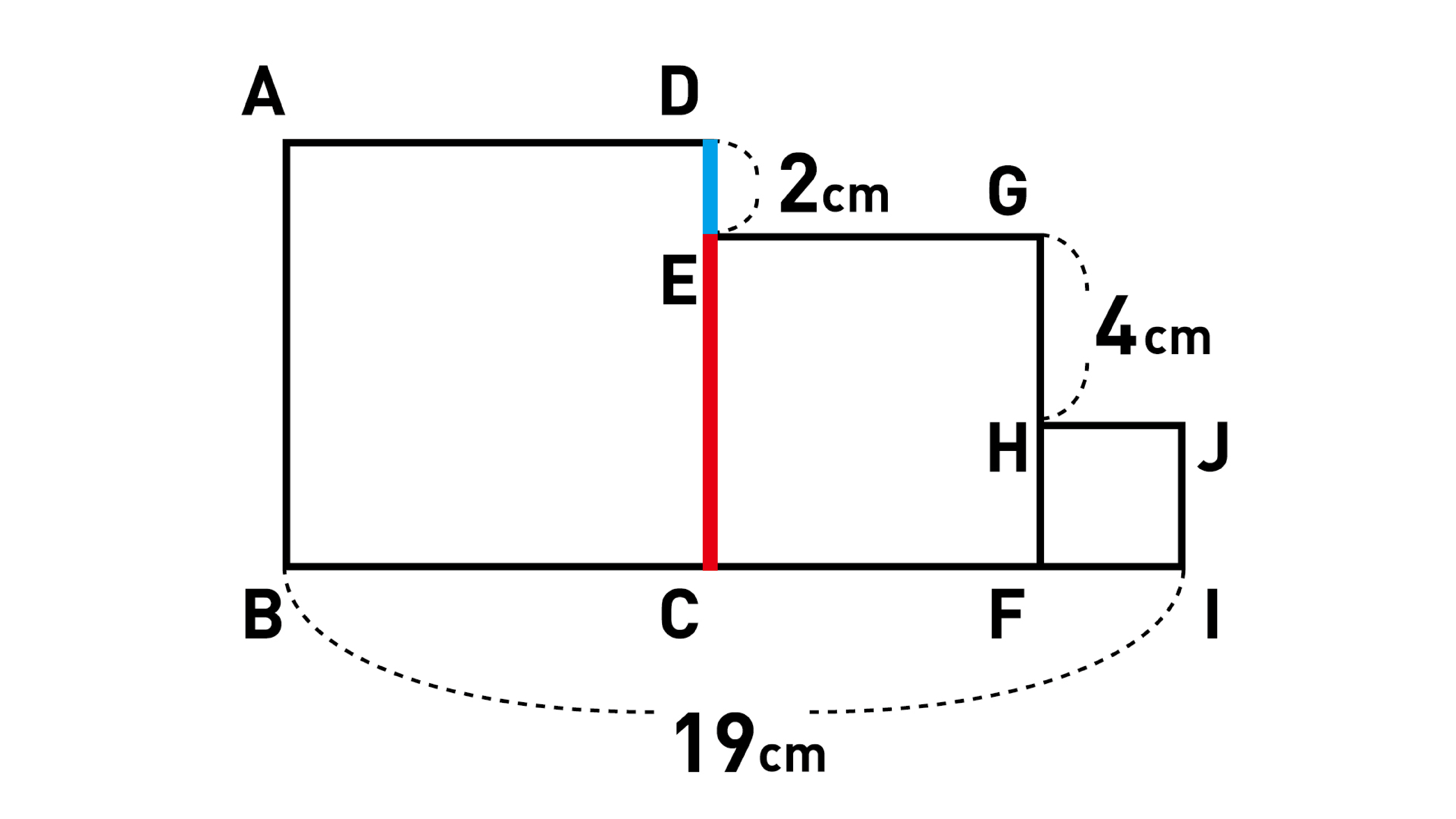
真ん中の正方形ECFGの一辺の長さを求める
設問の図では、辺BC+辺CF+辺FI=19cmです。
四角形ABCD、ECFG、HFIJはすべて正方形なので、辺BCと辺DC、辺FIと辺FHはそれぞれ同じ長さです。
これを用いると、以下の赤線のように辺DC+辺CF+辺FH=19cmとなります。
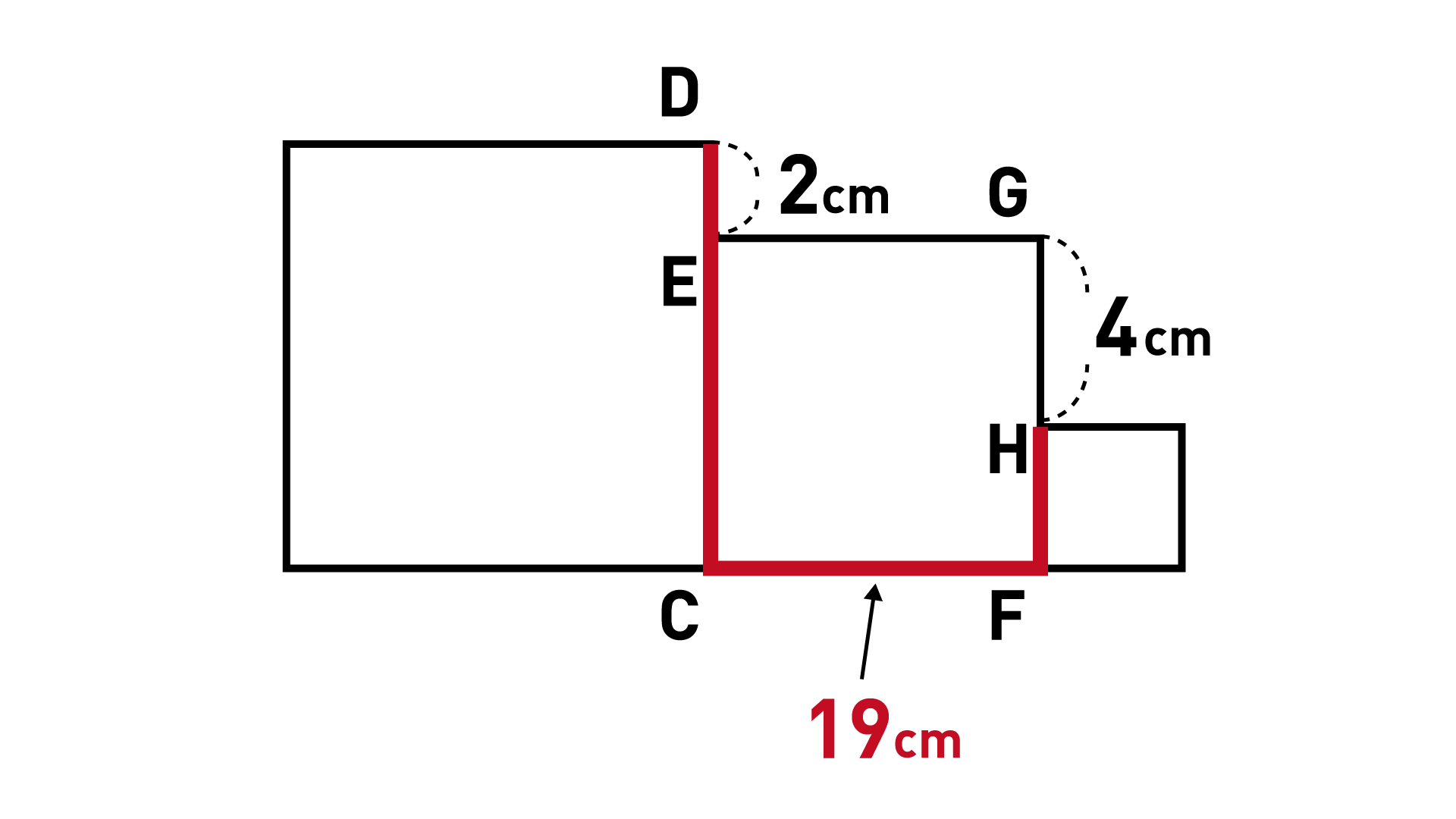
赤線の長さから線分DEの長さを引き、線分HGの長さを足すと、辺EC+辺CF+辺FGの長さになります。
なので、辺EC+辺CF+辺FGの長さは、19-2+4=21cmとなります。
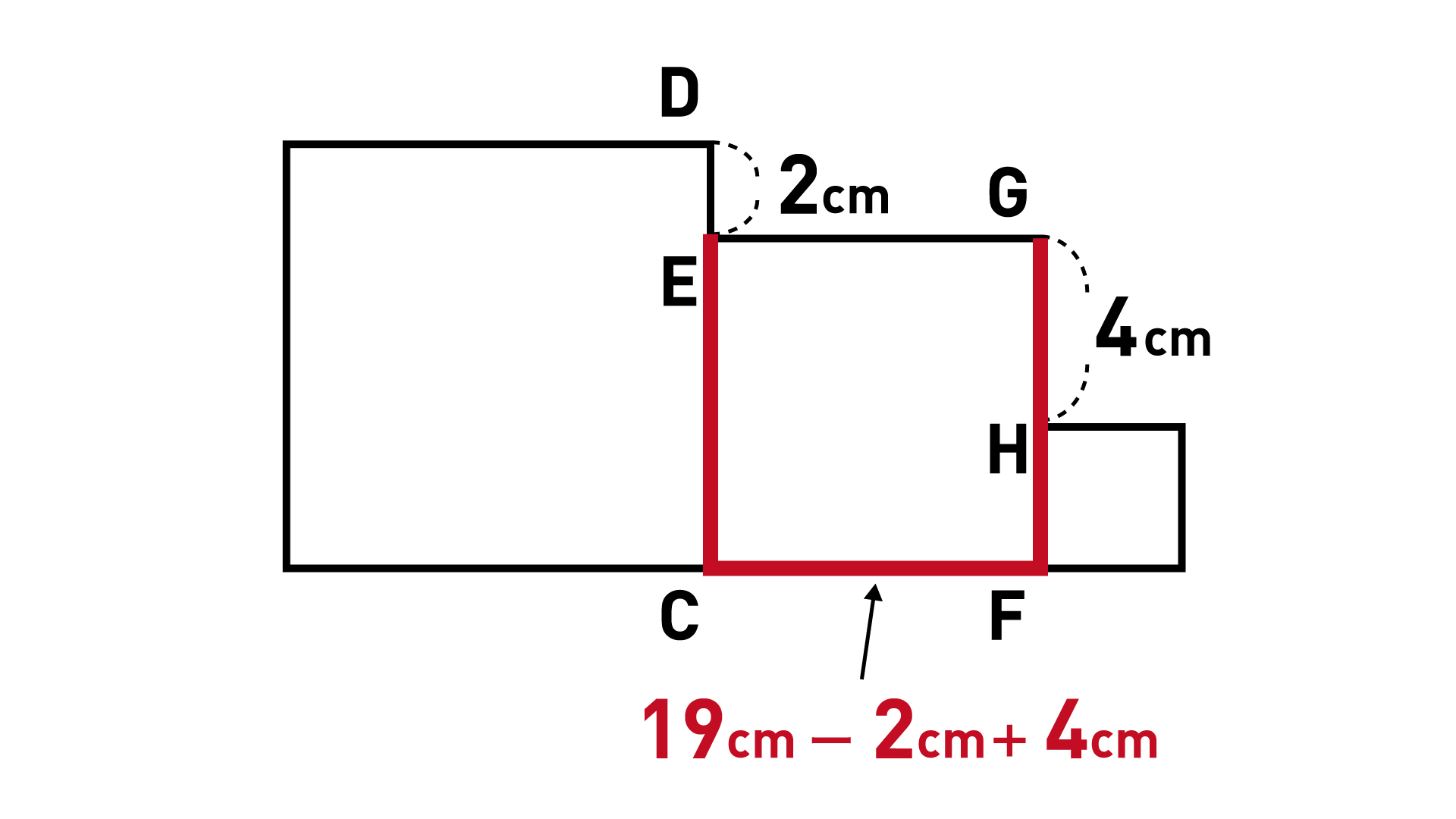
四角形ECFGは正方形であるため、辺EC、辺CF、辺FGは全て同じ長さです。
つまり、21cmを3で割った7cmが、真ん中の正方形ECFGの一辺の長さになります。
大きい正方形の面積を求める
大きい正方形ABCDの一辺は辺CDで、これは辺EC+辺DEの長さなので、7+2=9cm。
したがって、求めるべき正方形ABCDの面積は、9×9=81cm2となります。
答え:81cm2
難しそうな問題にぶち当たったときは、「答えを出すのに何が必要か」を考えると、案外うまくいくものです。
それでは。
【あわせて読みたい】










.jpg)










.jpg)







