解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
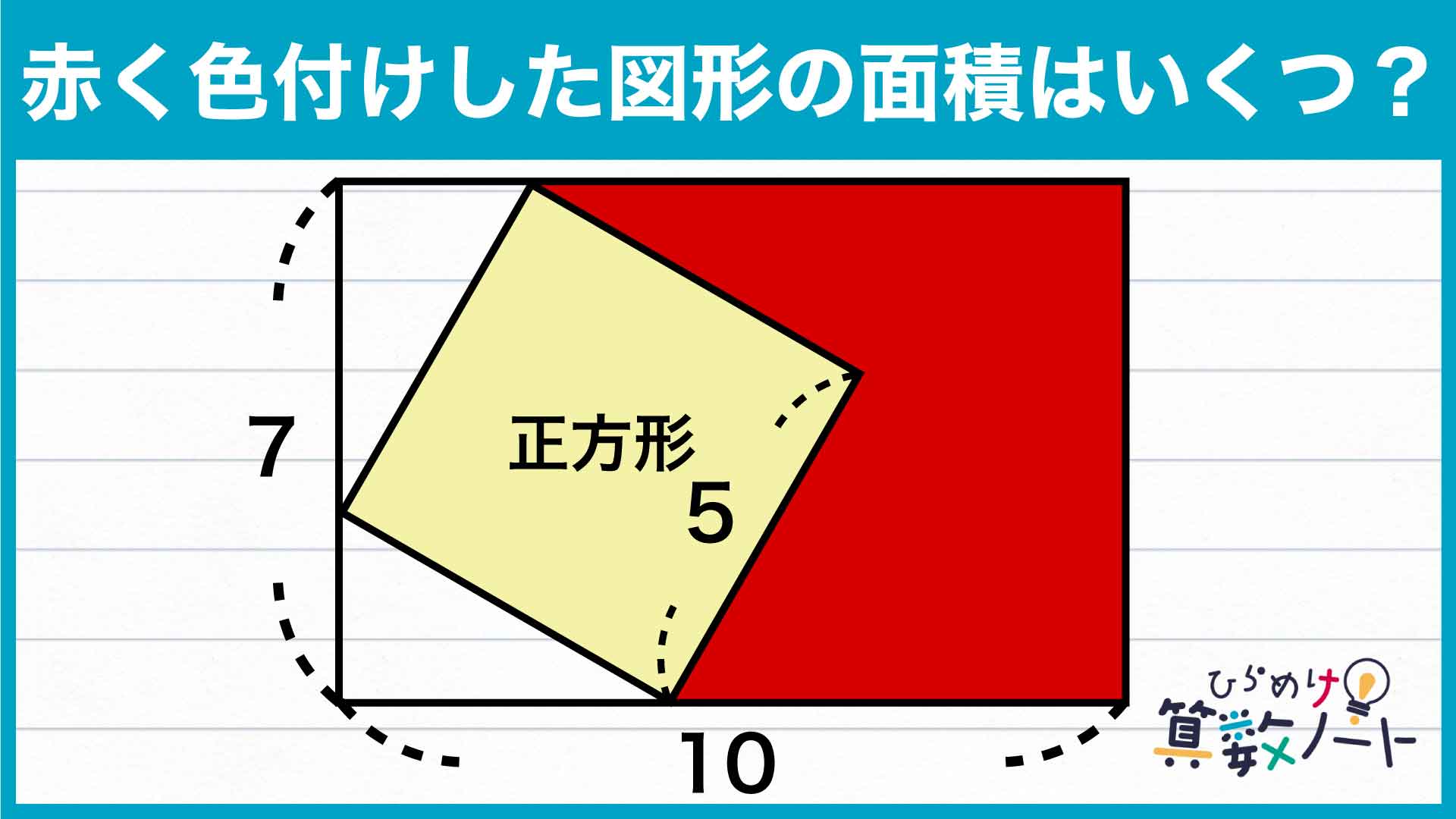
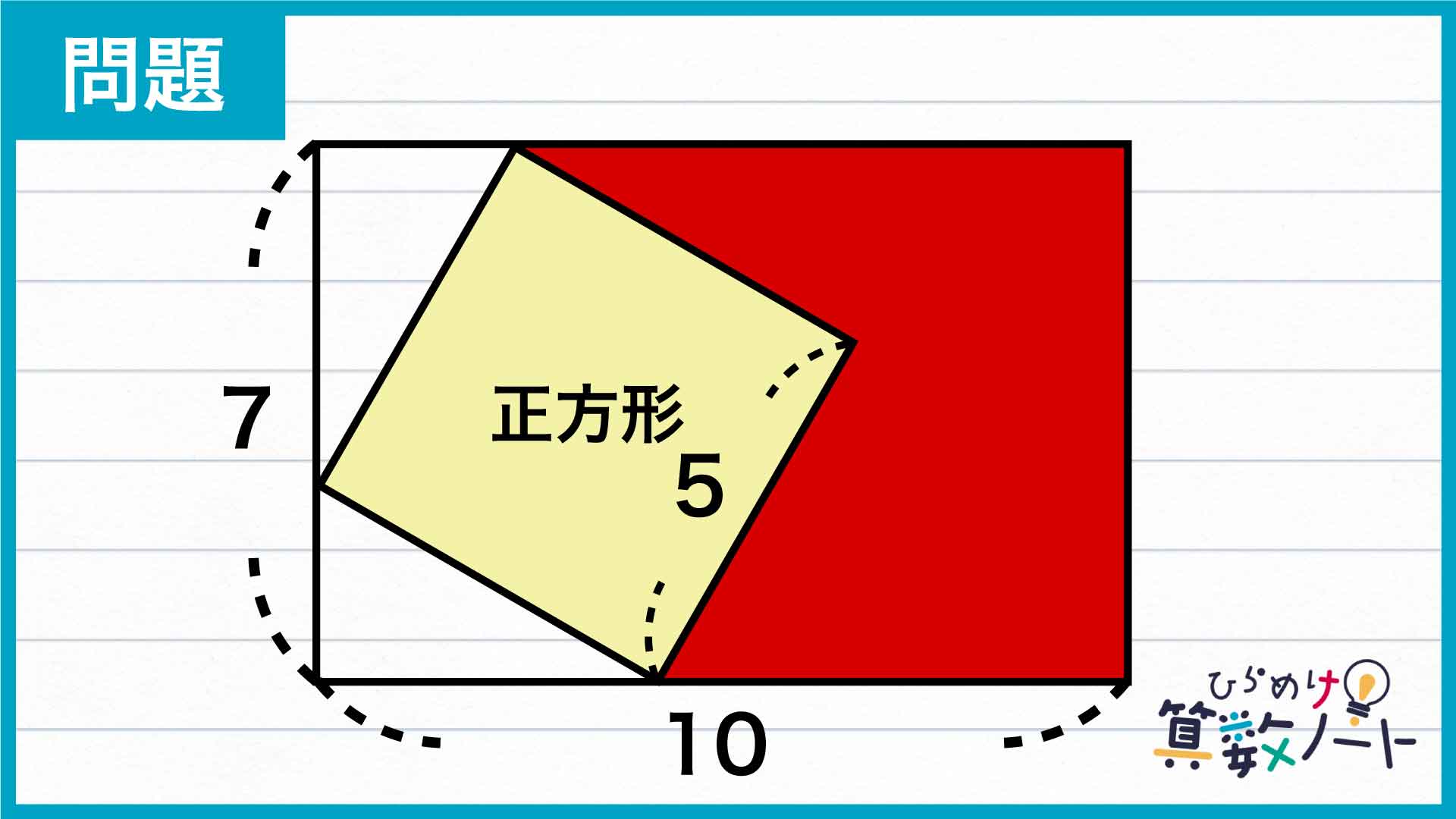
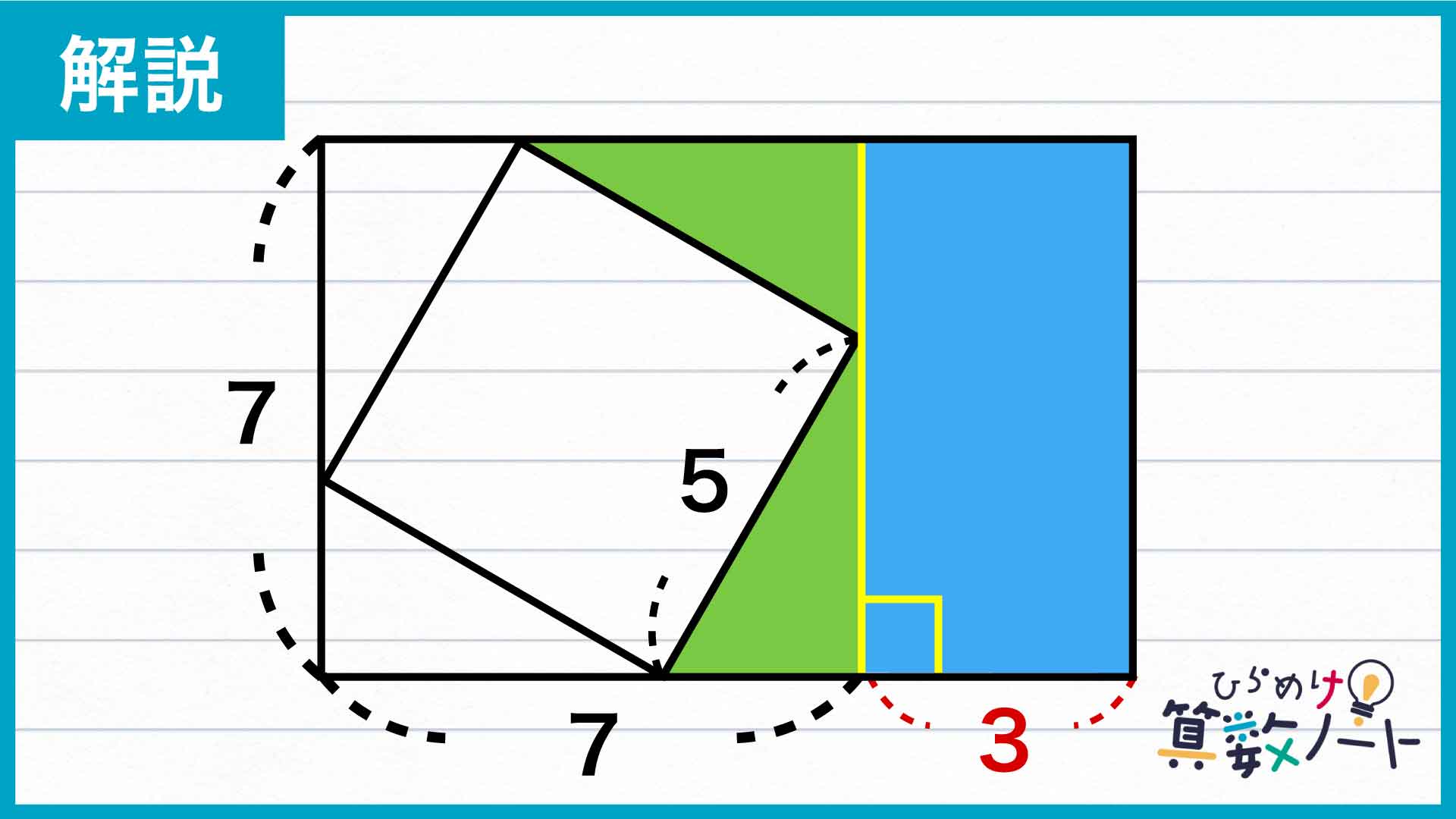
問題の解き方をまとめた図がこちらです。
ポイントは、補助線を引いて長方形全体を区切った上で、塗りつぶされた部分の面積をそれぞれ考えることです。
では、このポイントを踏まえつつ解いていきましょう!
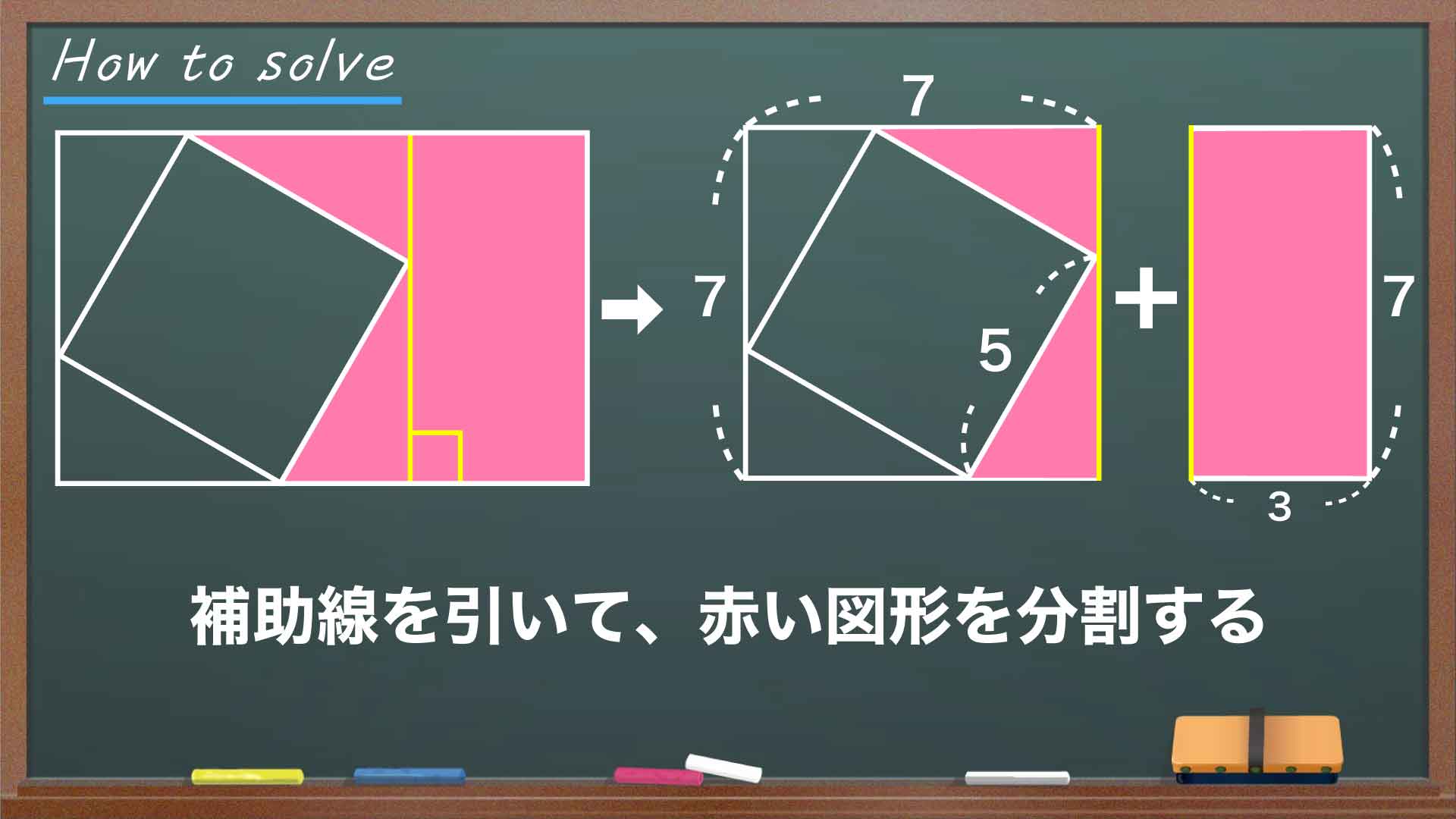
補助線を引く
塗りつぶされた部分は形がやや複雑なため、面積を求めるときにはよりシンプルな図形に分ける必要があります。
正方形の頂点を通り、長方形の長辺に垂直な補助線を引くと、塗りつぶされた部分は2つの直角三角形と1つの長方形に分かれます。これらの面積を求めて足し合わせることで、答えに行き着くことができます。
直角三角形2つの面積を求める
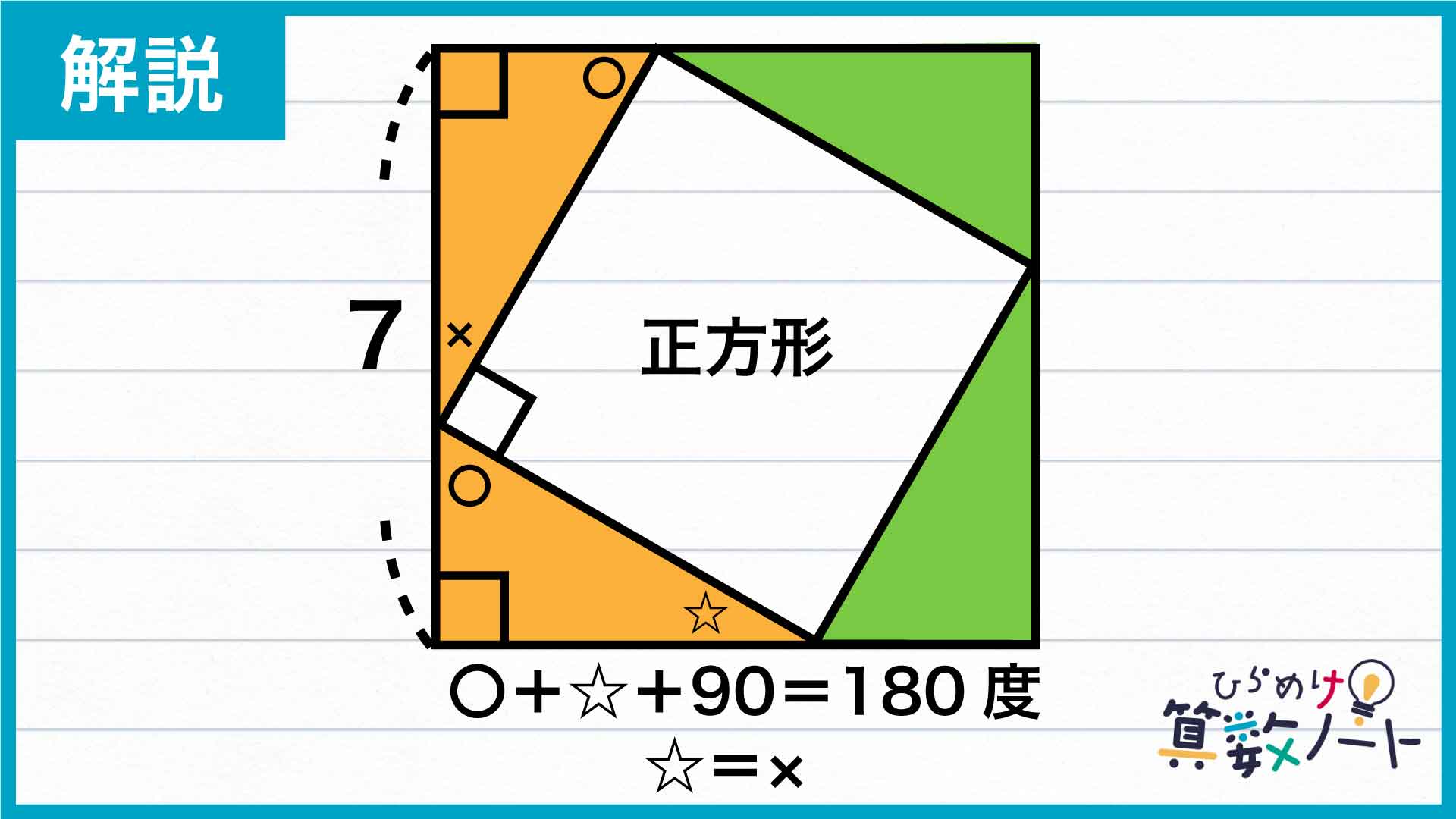
まずは、補助線より左側の部分に注目します。左上の直角三角形について、図のように直角以外の角をそれぞれ〇、×とおくと、三角形の内角の合計は180度なので、〇+×+90=180度であることがわかります。
ここで、下の図のように、左下の直角三角形で★をつけた角の大きさを考えます。左上の直角三角形で×をつけた角、正方形の直角、および★をつけた角を足し合わせると180度になることから、★と〇の角の大きさは同じであることがわかります。
また、下の図で☆を付けた角について、三角形の内角の合計は〇+☆+90=180度であることから、☆と×の角の大きさは同じになります。
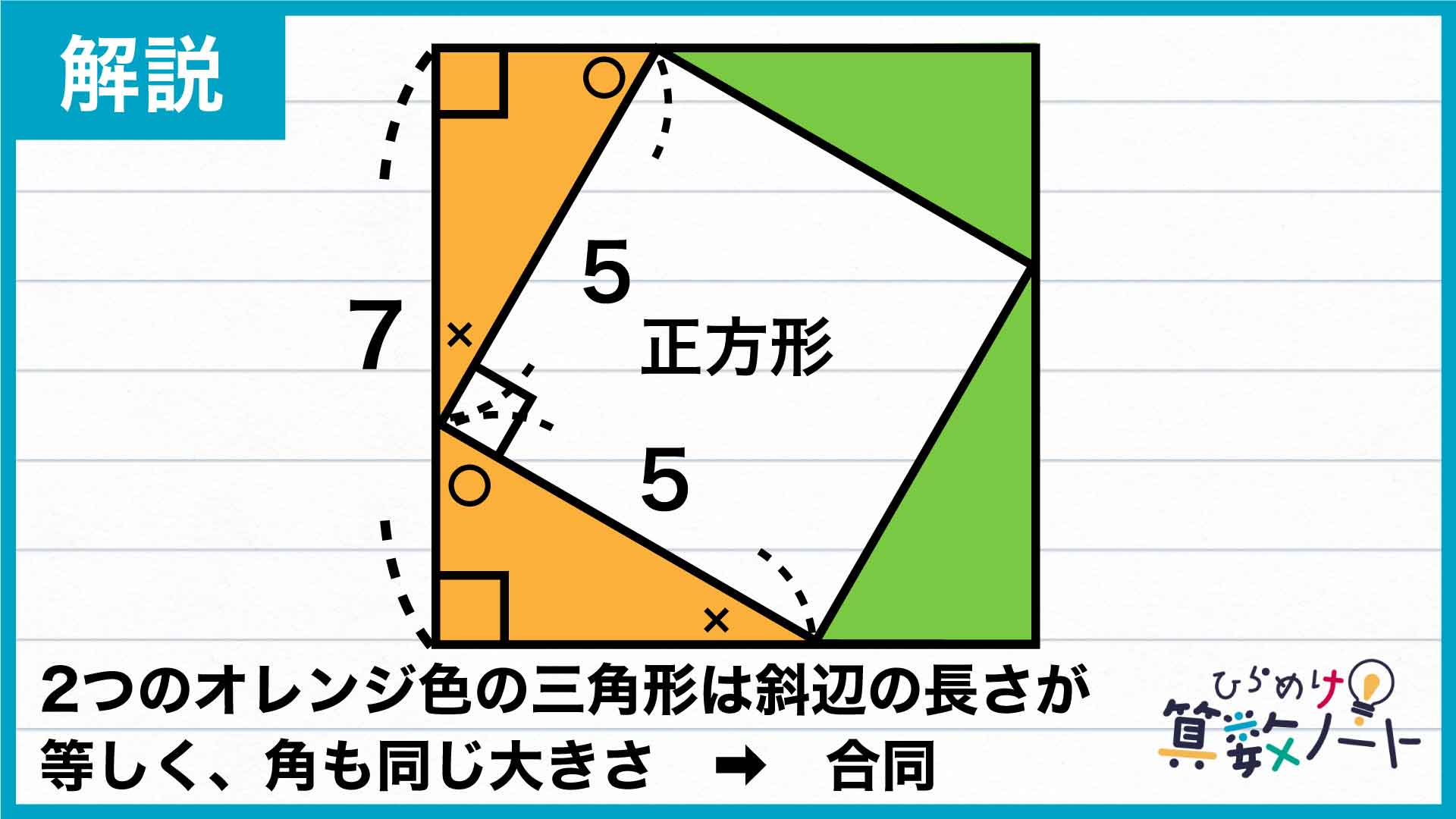
さらに、斜辺の長さは5で等しいことから、2つの直角三角形は合同であることがわかりました。
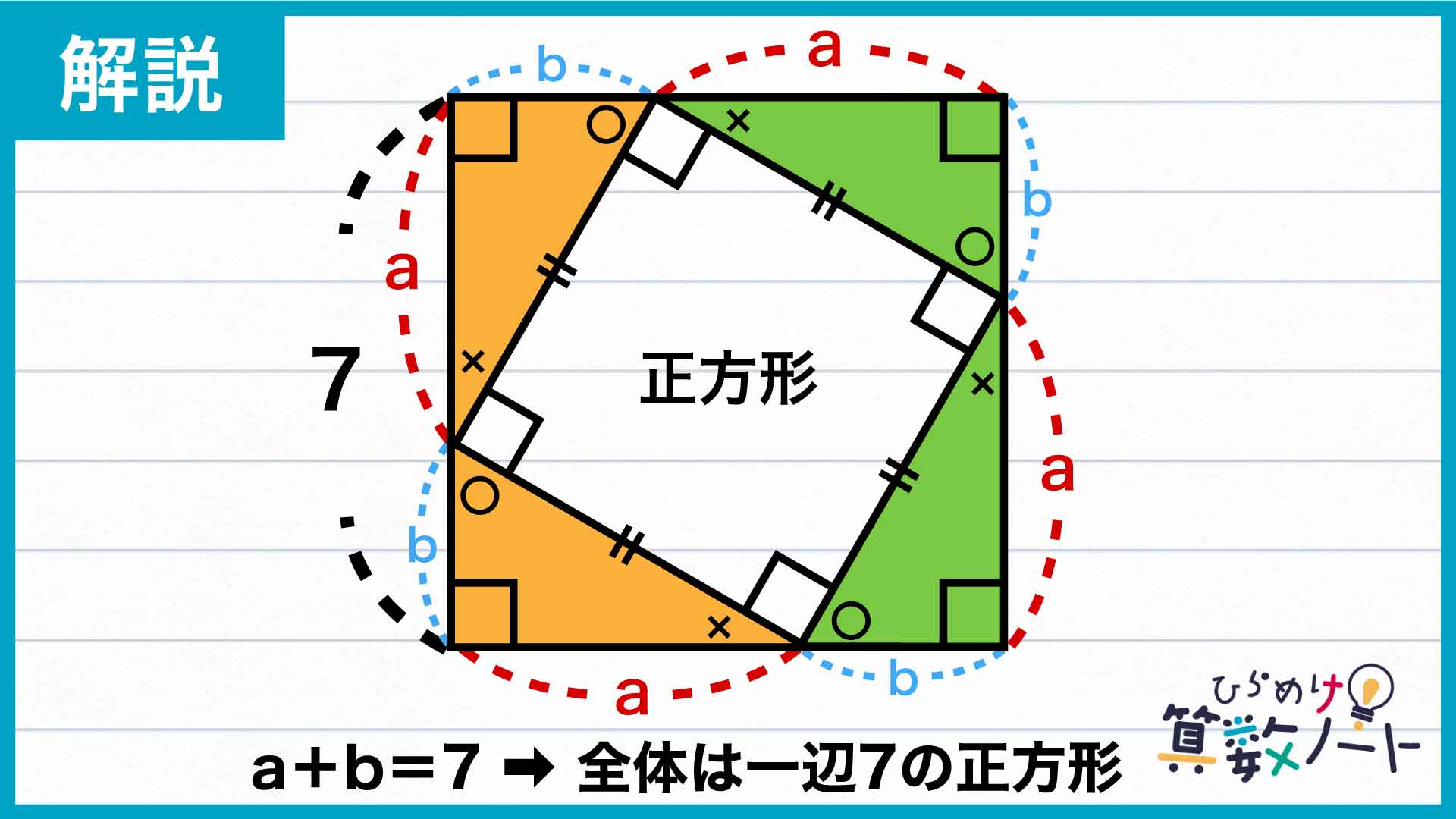
同じように考えれば、4つの直角三角形は全て合同。直角を挟んだ辺の長さをそれぞれa、bとすると、大きな四角形のすべての辺についてa+b=7が成り立つので、大きな四角形は一辺7の正方形であるとわかります。
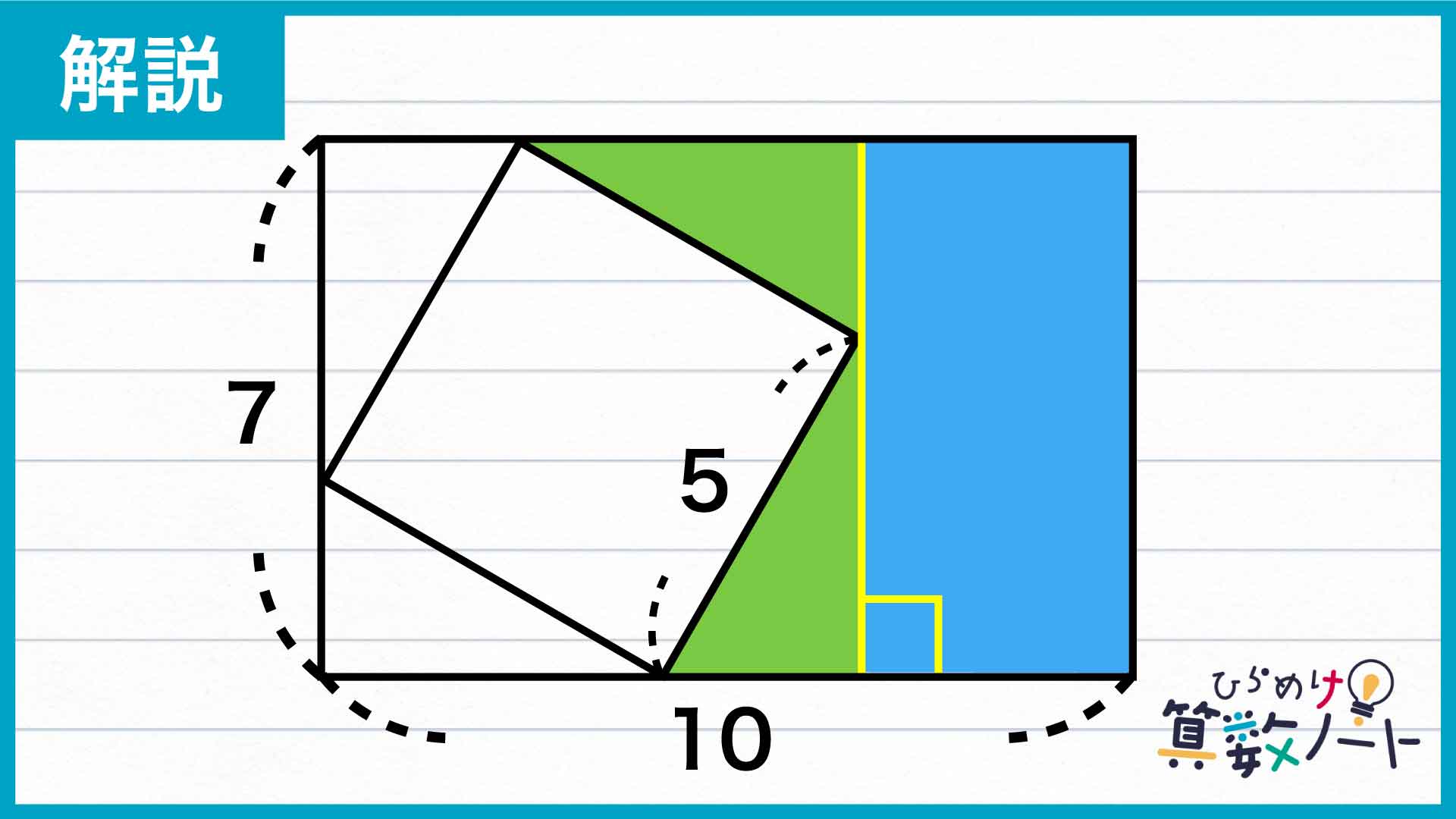
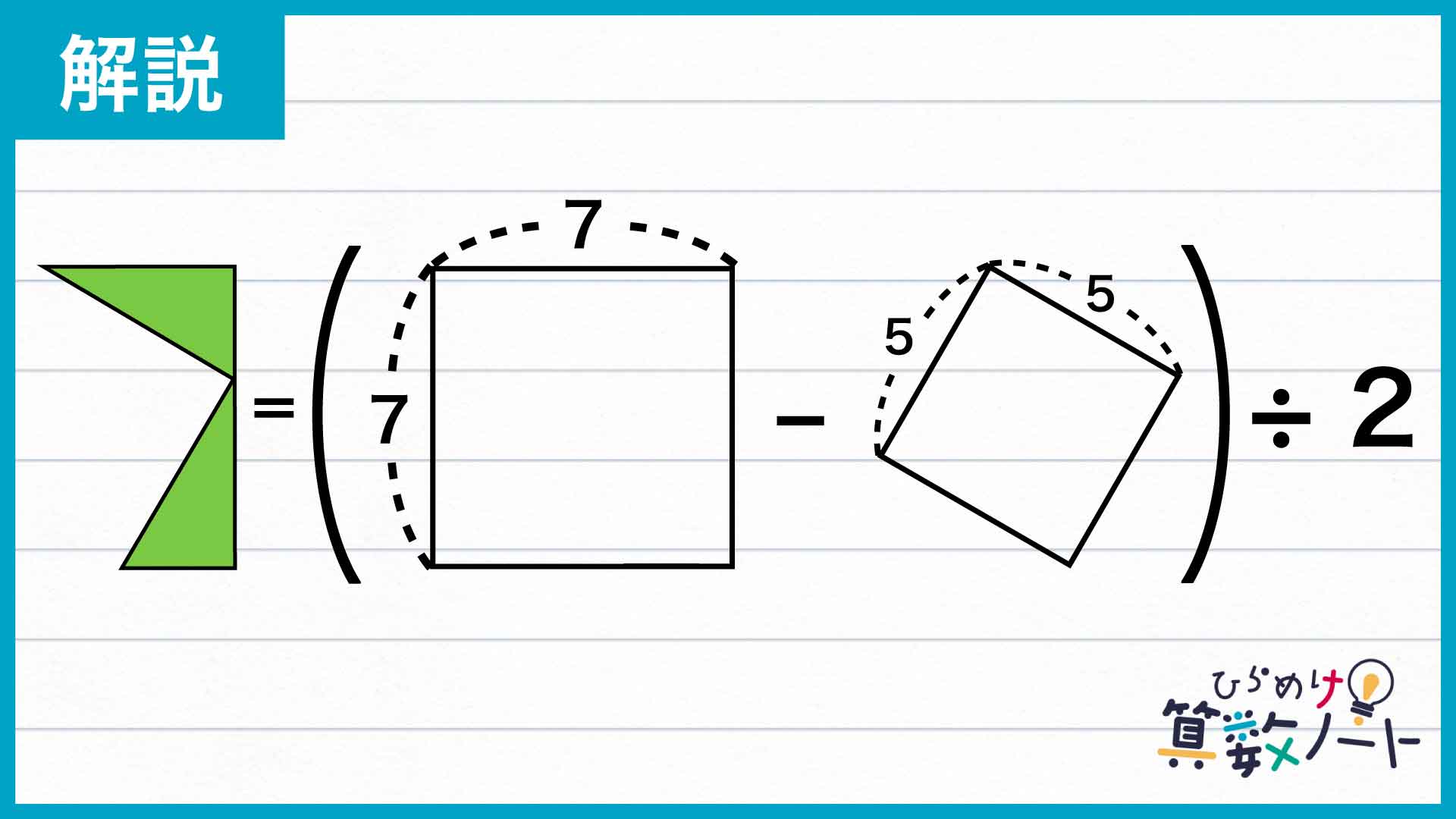
つまり、塗りつぶされた部分の面積は、一辺7の正方形から一辺5の正方形を引いて残った面積の半分ということになるのです。
したがって、塗りつぶされた部分のうち左側の面積は、(7×7-5×5)÷2=12です。
長方形の面積を求めて足す
次に、右側の長方形です。左側の図形が一辺7の正方形なので、長方形の横の辺の長さは10-7=3です。縦の長さは左側の正方形の一辺の長さと同じく7なので、右側の長方形の面積は、3×7=21とわかりました。
以上より求める面積は、直角三角形2つと長方形1つの面積の合計なので、12+21=33となります。
答え:33
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)









.jpg)






