解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
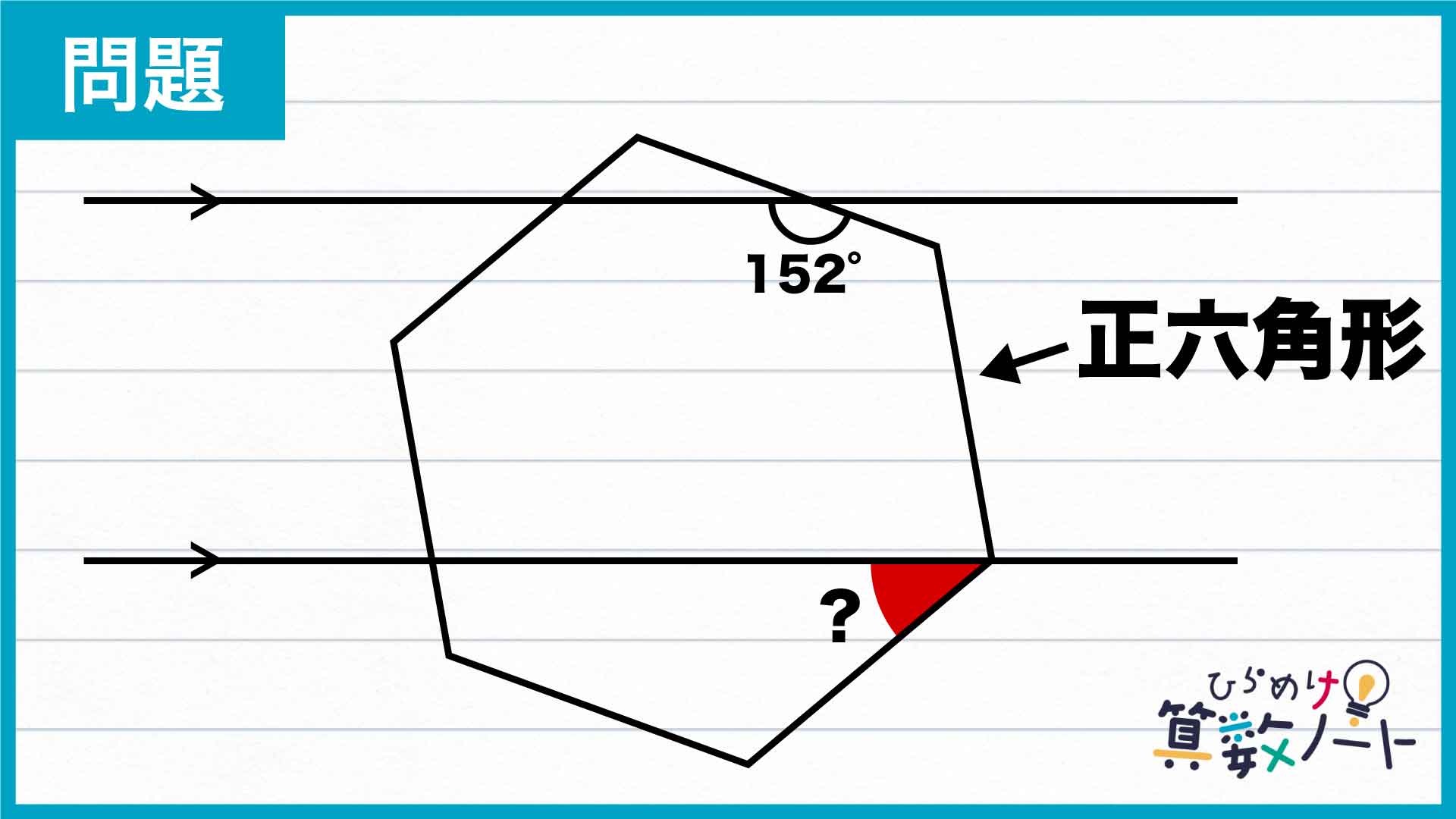
前ページ:自力で解きたい方はこちらへ!以下は問題の解説です。
今回の問題を解くうえで重要なポイントを以下にまとめました。
整理すると、
- 図に補助線を引く
- 錯角の関係を利用する
- 正六角形のひとつの内角の大きさが120度であることを利用する
の3点です。これらのポイントをふまえたうえで、問題を解いていきましょう!
正六角形の頂点を通る平行線を書く
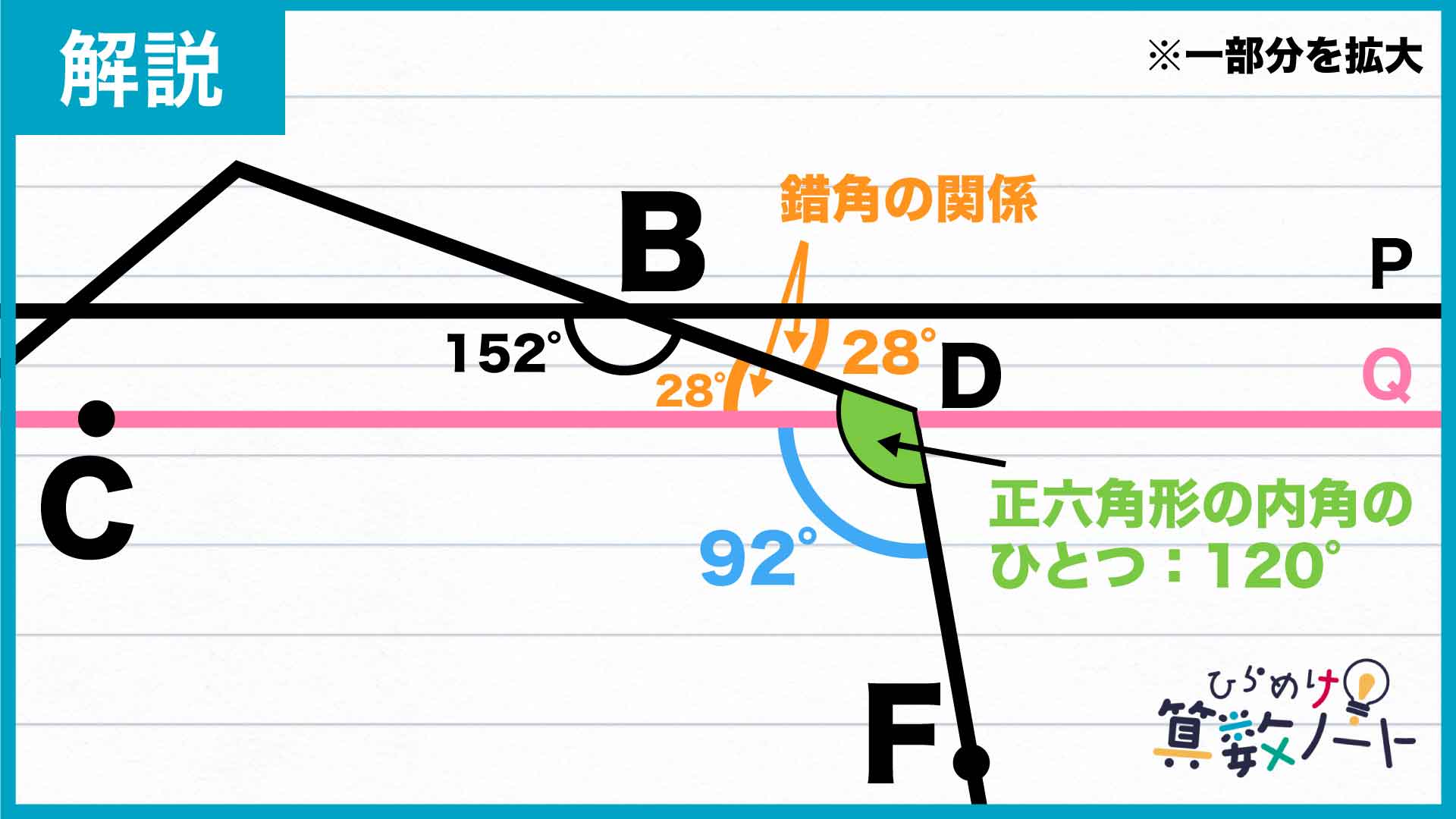
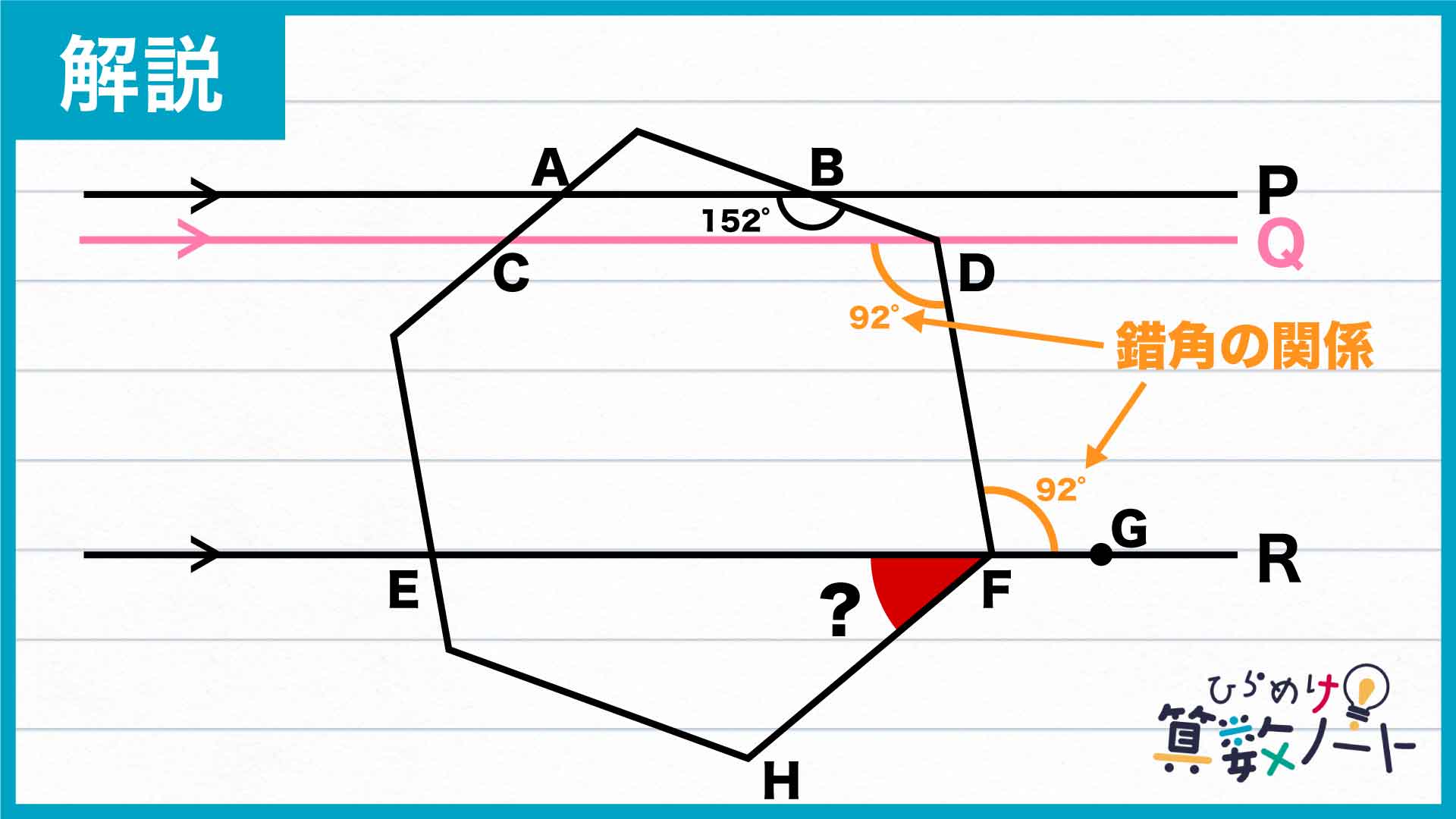
下の図のように、問題の図に平行線を1本書き足します。また、わかりやすくするために点Aから点Hまでの点を振っておきます。
平行線についての錯角の関係と、正六角形の性質を使う
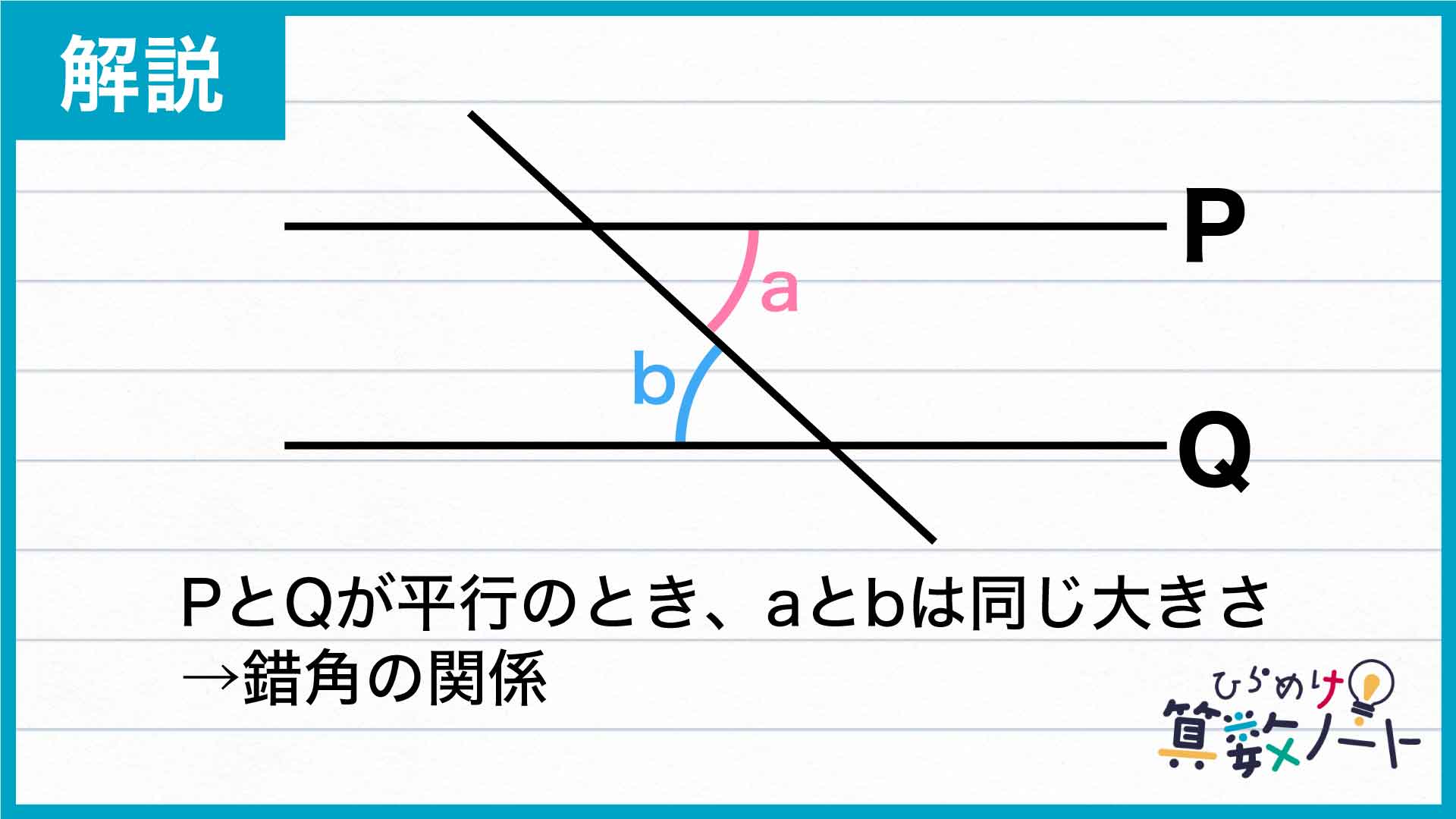
まず、平行線Pと平行線Qに注目しましょう。ここで、2本の平行線について次の性質を使います。
この性質を使うと、角BDCの大きさは28度であることがわかります。
さらに、正六角形のひとつの内角の大きさが120度であることを使うと、角BDC+角FDC=120度となるので、角FDCの大きさは120-28=92度であることがわかります。
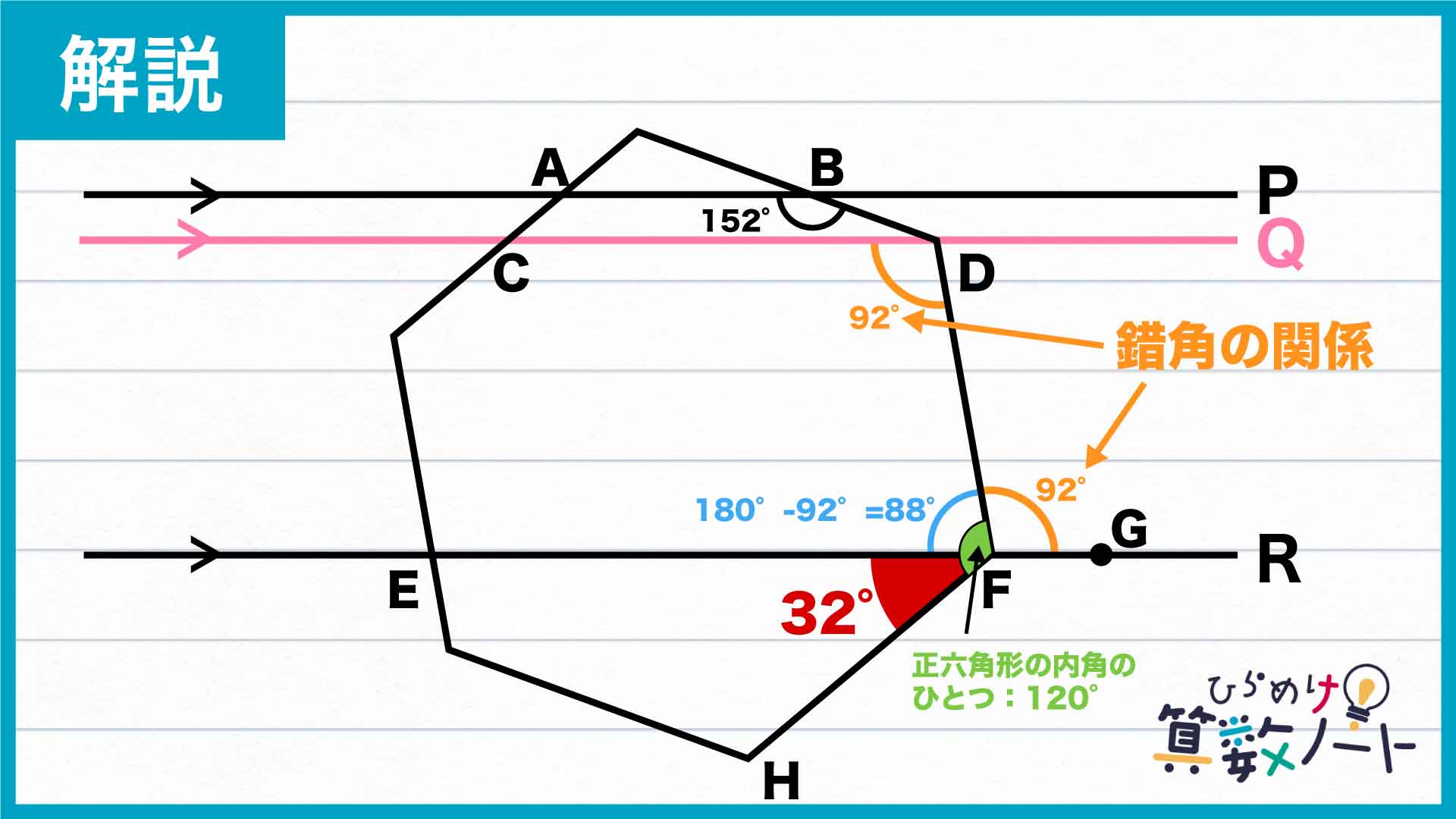
次に、平行線Qと平行線Rに注目します。さきほどと同じように、平行線についての錯角の関係を使うと、角FDCと角DFGの大きさは同じになります。よって、角DFGの大きさは92度になります。
また、角DFEの大きさは180-92=88度であることがわかります。
最後に、もう一度正六角形のひとつの内角の大きさが120度であることを使いましょう。すると、角DFHの大きさが120度となり、角DFE+角EFH=120度になります。よって、赤く色付けした角の大きさは120-88=32度となります。
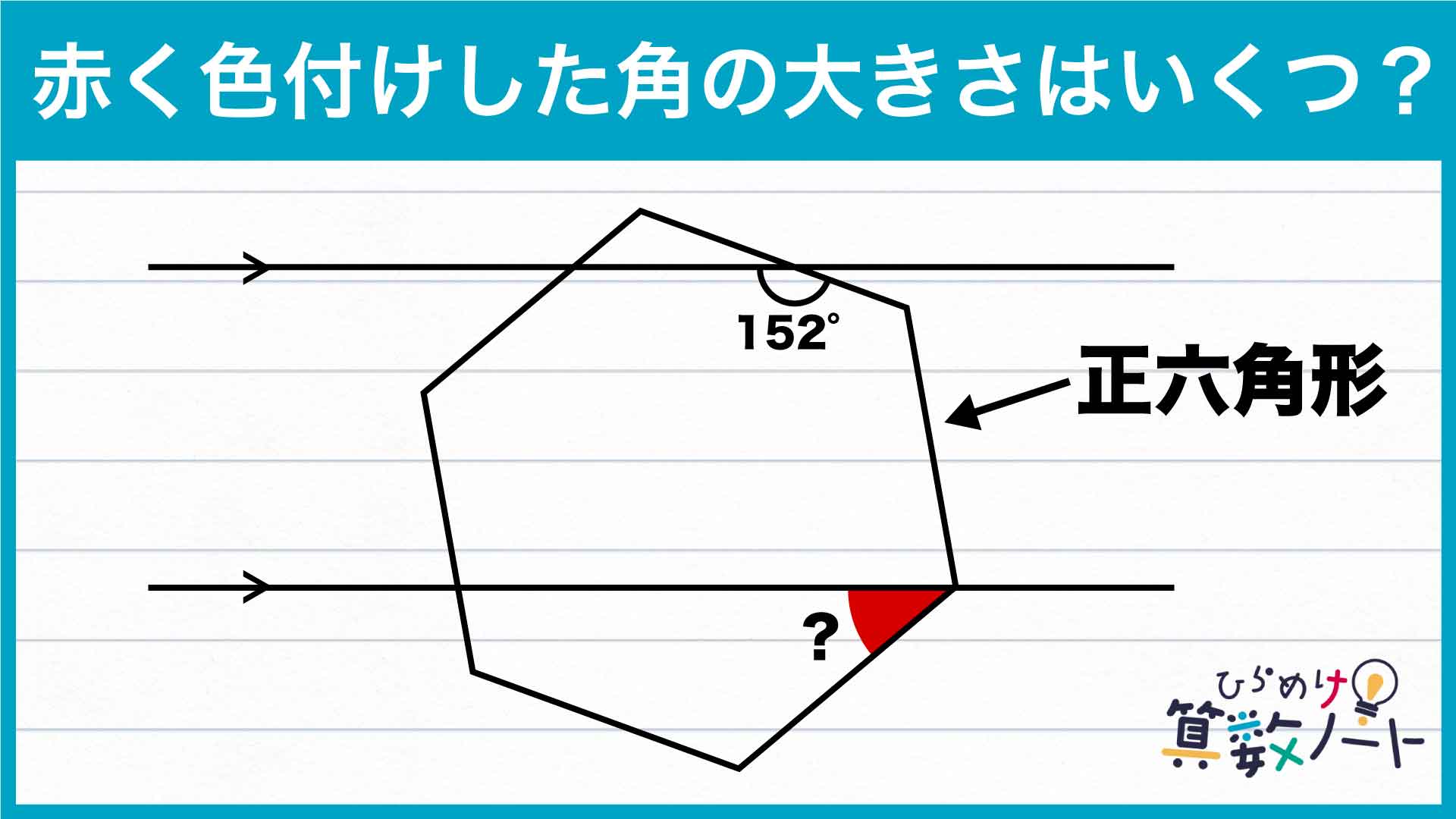
答え:32度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)







.jpg)






