解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
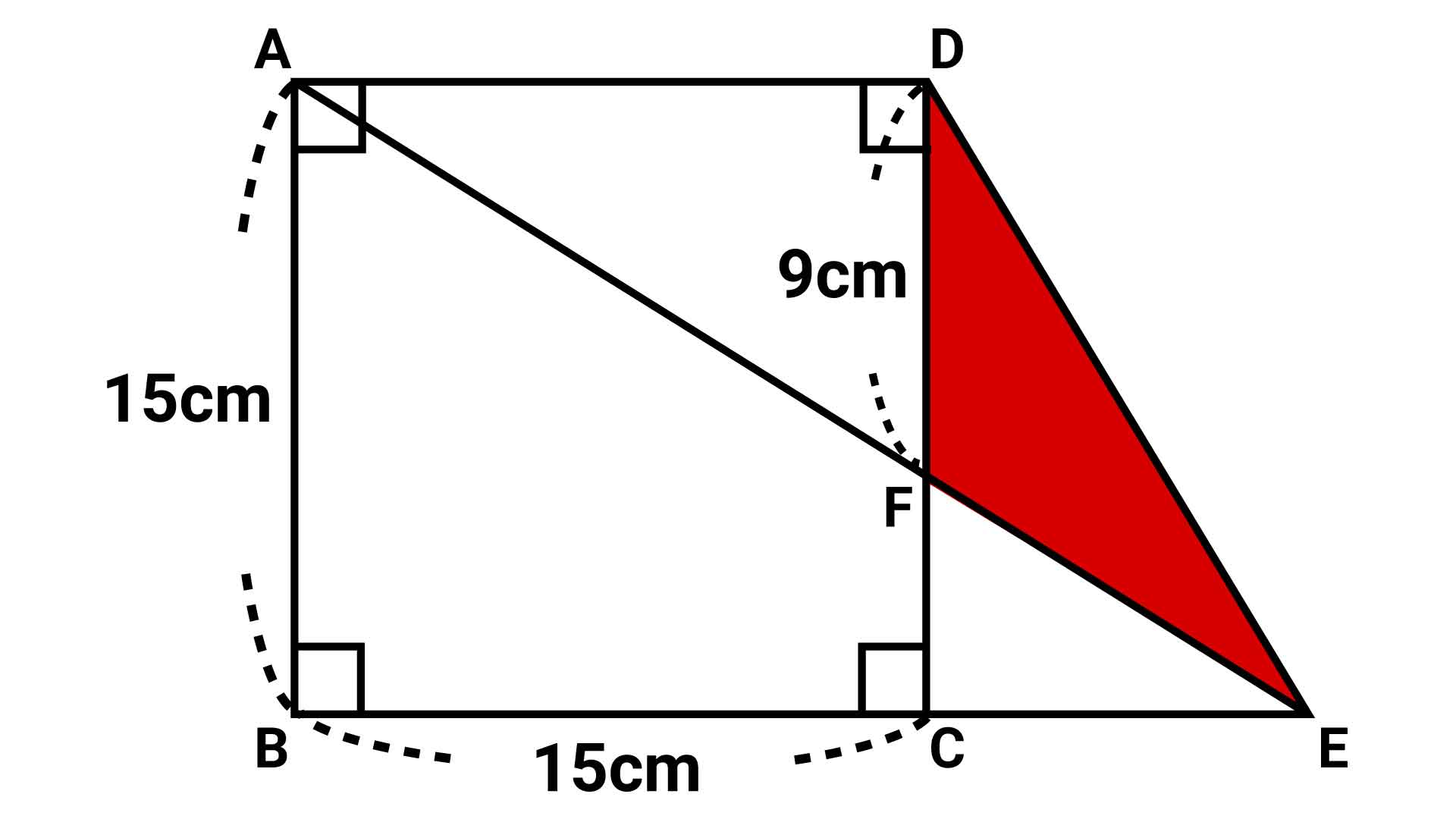
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引き、面積が同じ1対の三角形を見つけ、それらの共通部分を取り除くことです。
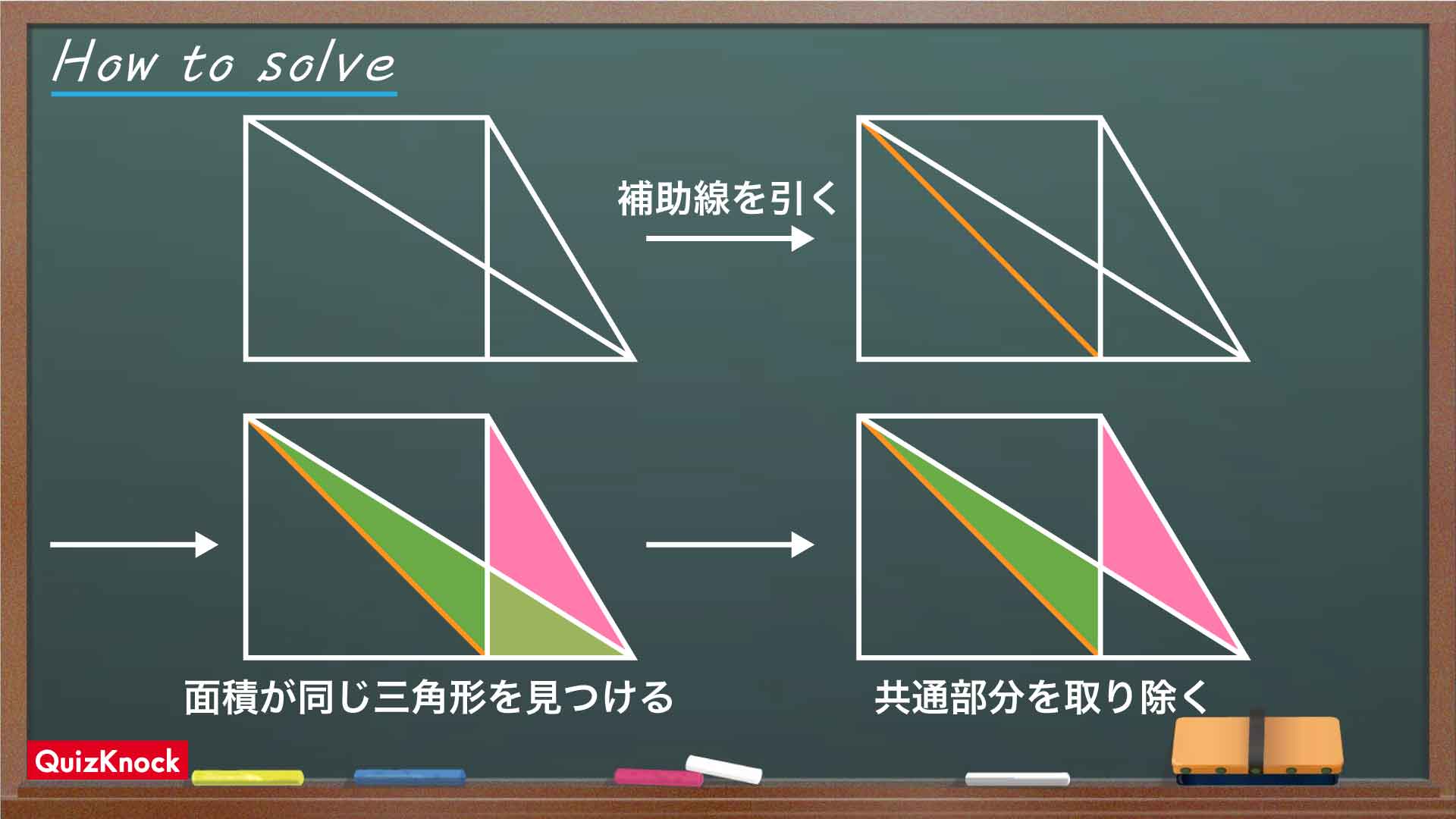
この図の流れに沿って、解いていきましょう!
補助線を引くと……
まずは、この問題を解きやすくする補助線として、対角線ACを引きます。
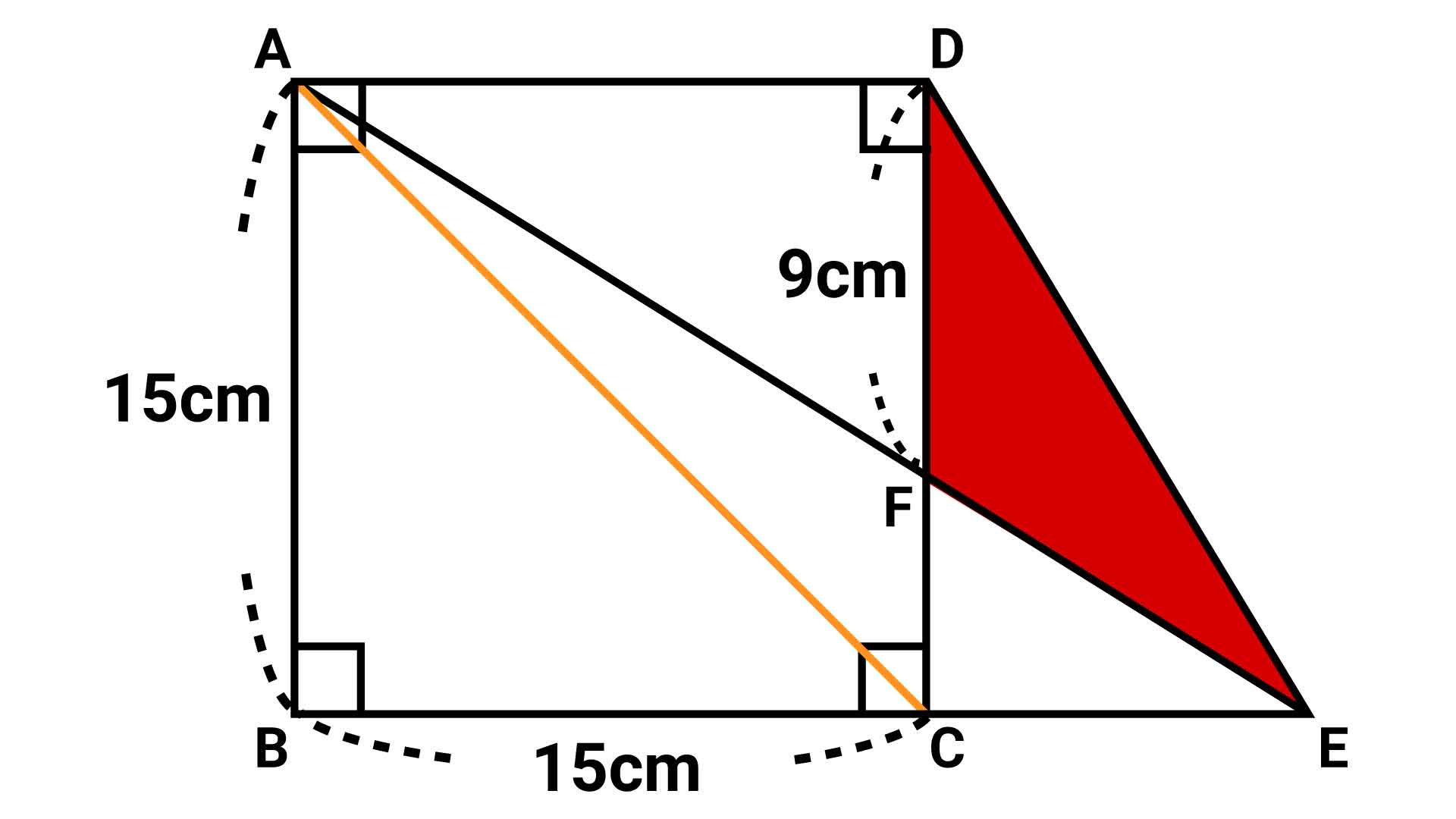
そして、以下の図の3つの三角形(a〜c)に着目します。
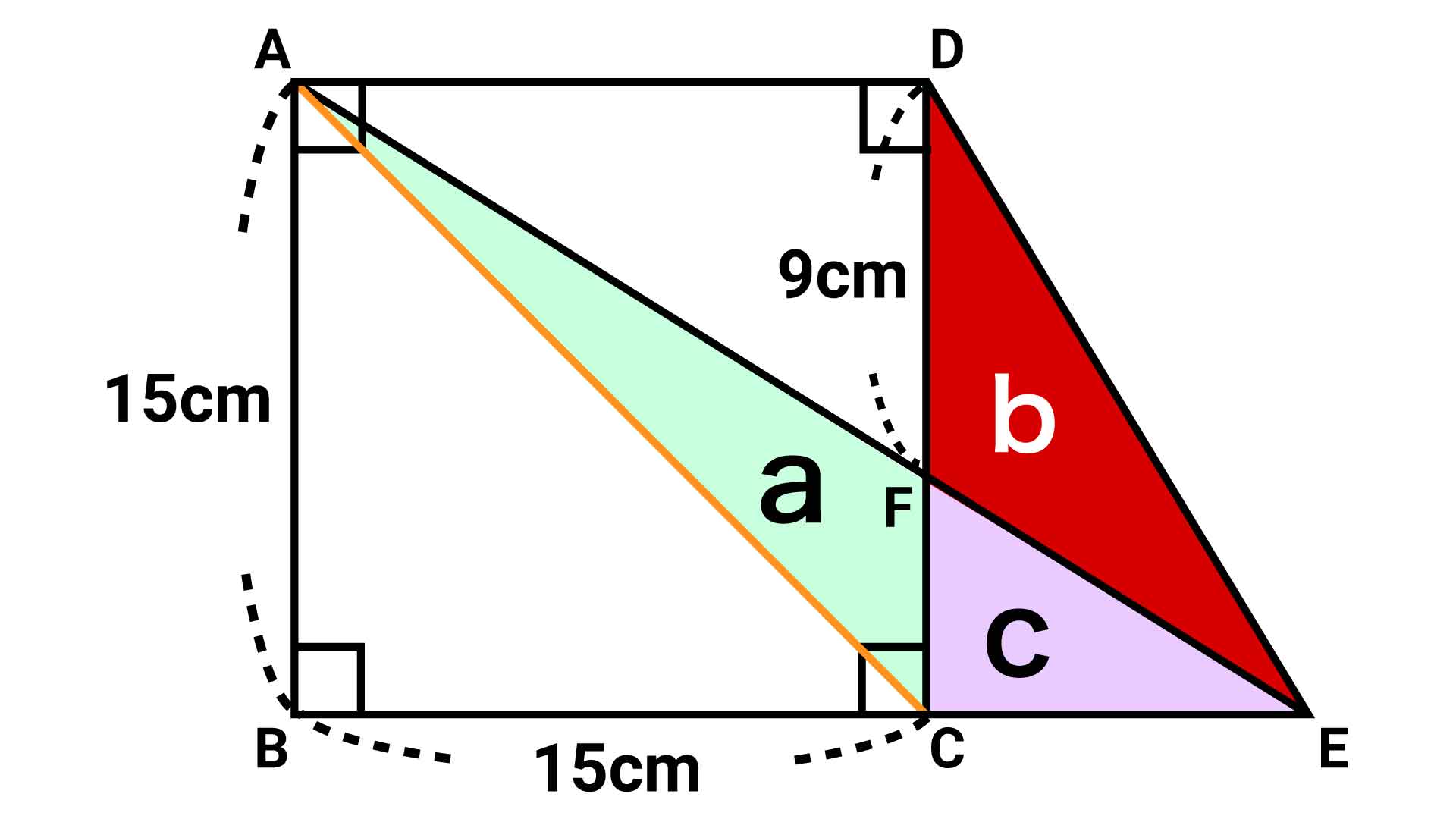
このうち、aとcを組み合わせた三角形と、bとcを組み合わせた三角形を見比べると、底辺(辺CE)を共有しており、高さも等しいため、面積は等しくなっています。
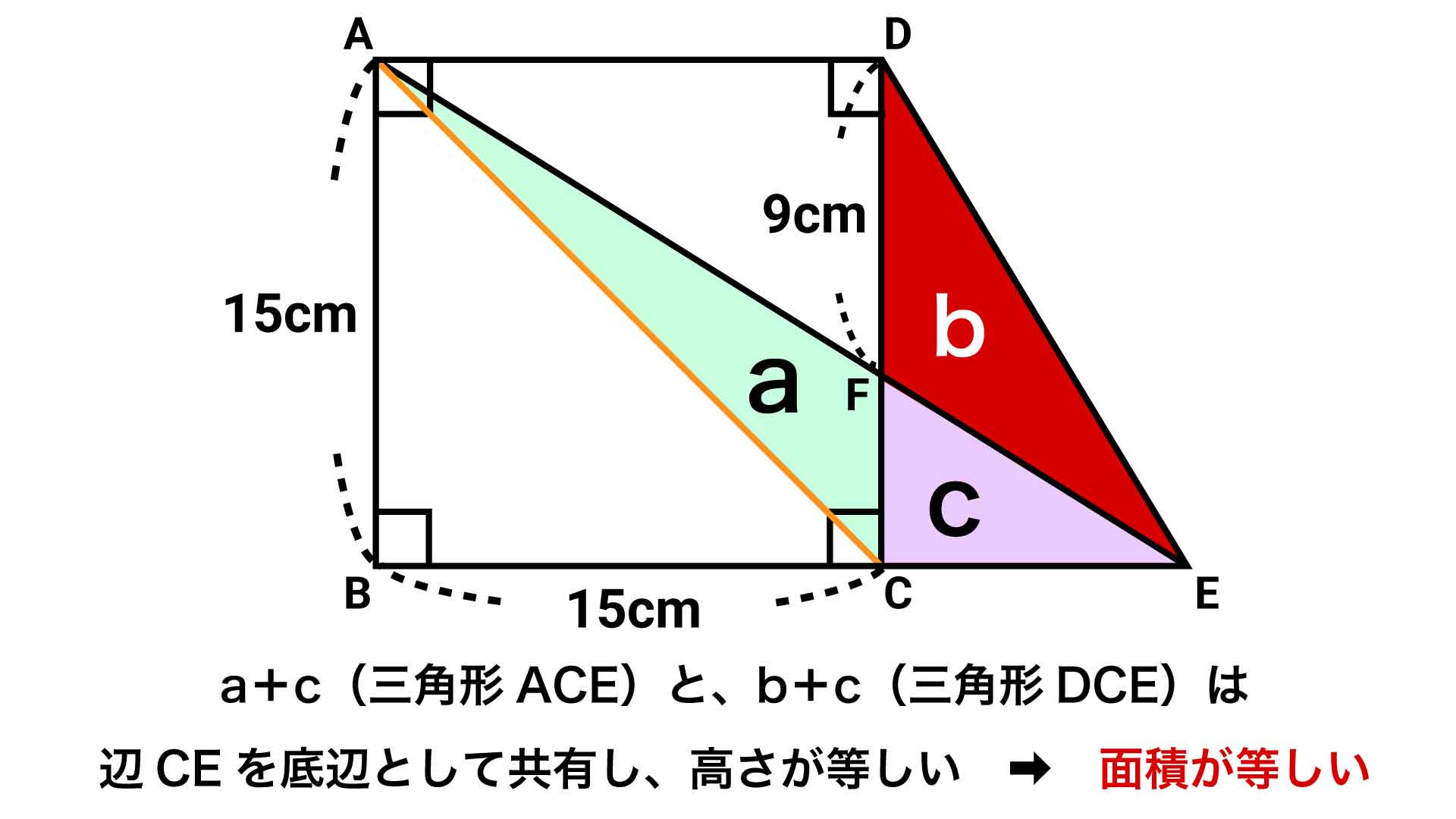
2つの三角形の共通部分を取り除く
aとcを組み合わせた三角形と、bとcを組み合わせた三角形の面積が等しいことがわかりました。どちらも三角形cを含んでいることから、三角形aと三角形bの面積が等しいことがわかります。
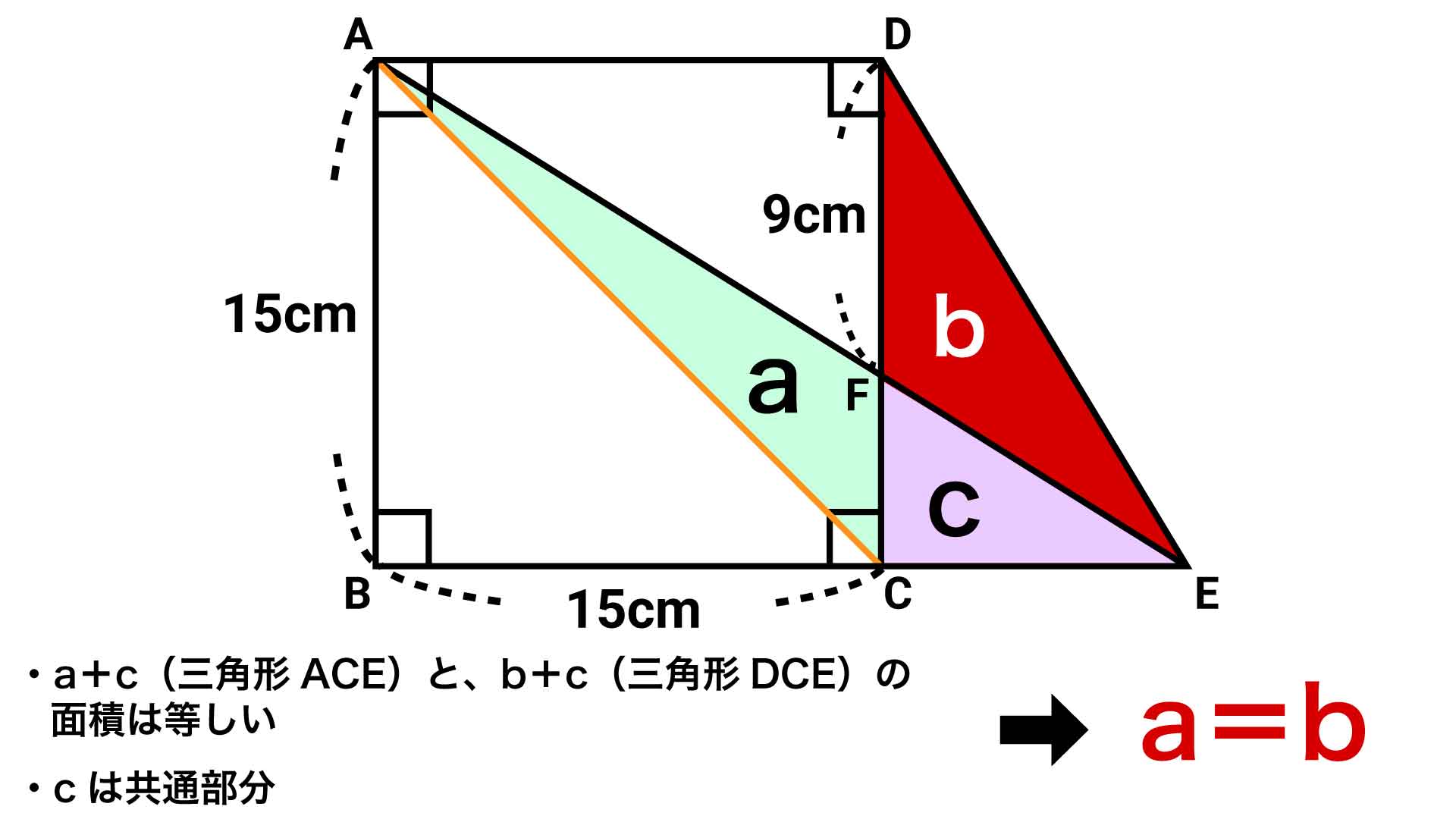
aの面積を求める
三角形aの面積は、辺CFを底辺としてみると、(底辺)×(高さ)÷2という公式を用いて求めることができます。
辺CFの長さは、15-9=6cmであることから、三角形aの面積は、6×15÷2=45cm2となります。
したがって、三角形b、すなわち三角形DEFの面積も45cm2です。
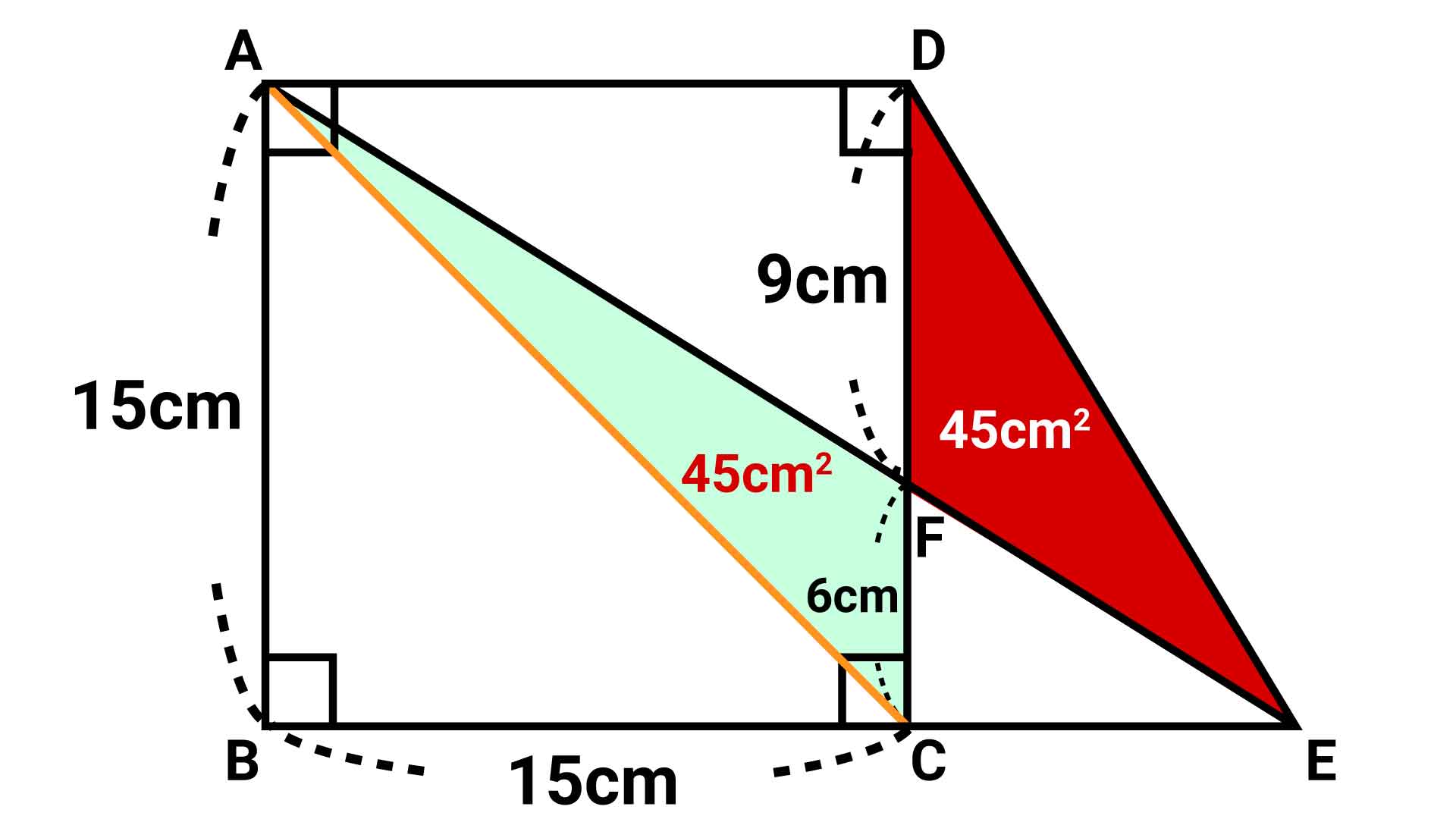
答え:45cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)










.jpg)







