解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回の解き方をまとめた図がこちらです。
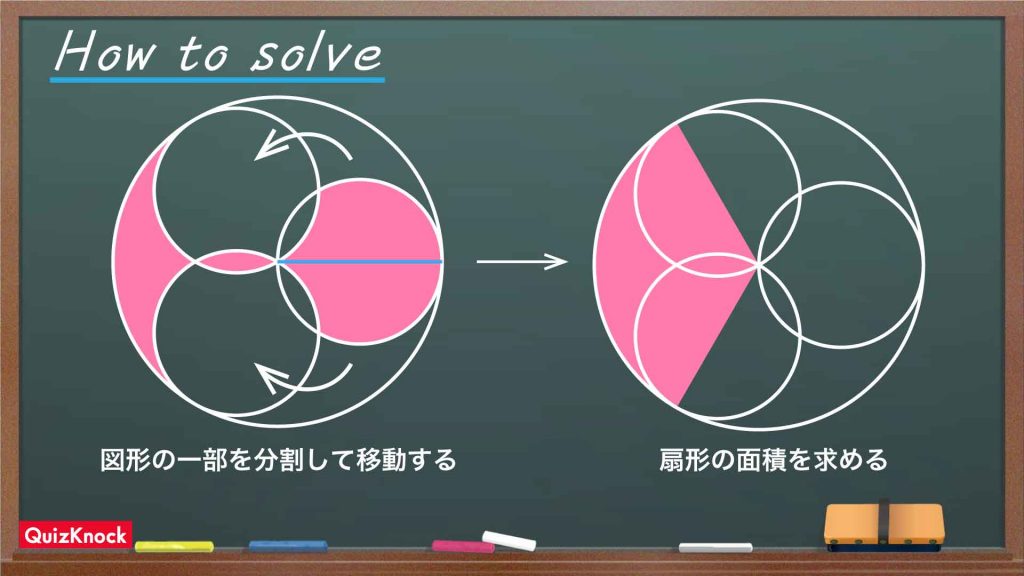
今回のポイントは、赤色の図形を「面積を求めやすい形に変形する」ことです。
この流れに沿って、問題を攻略していきましょう!
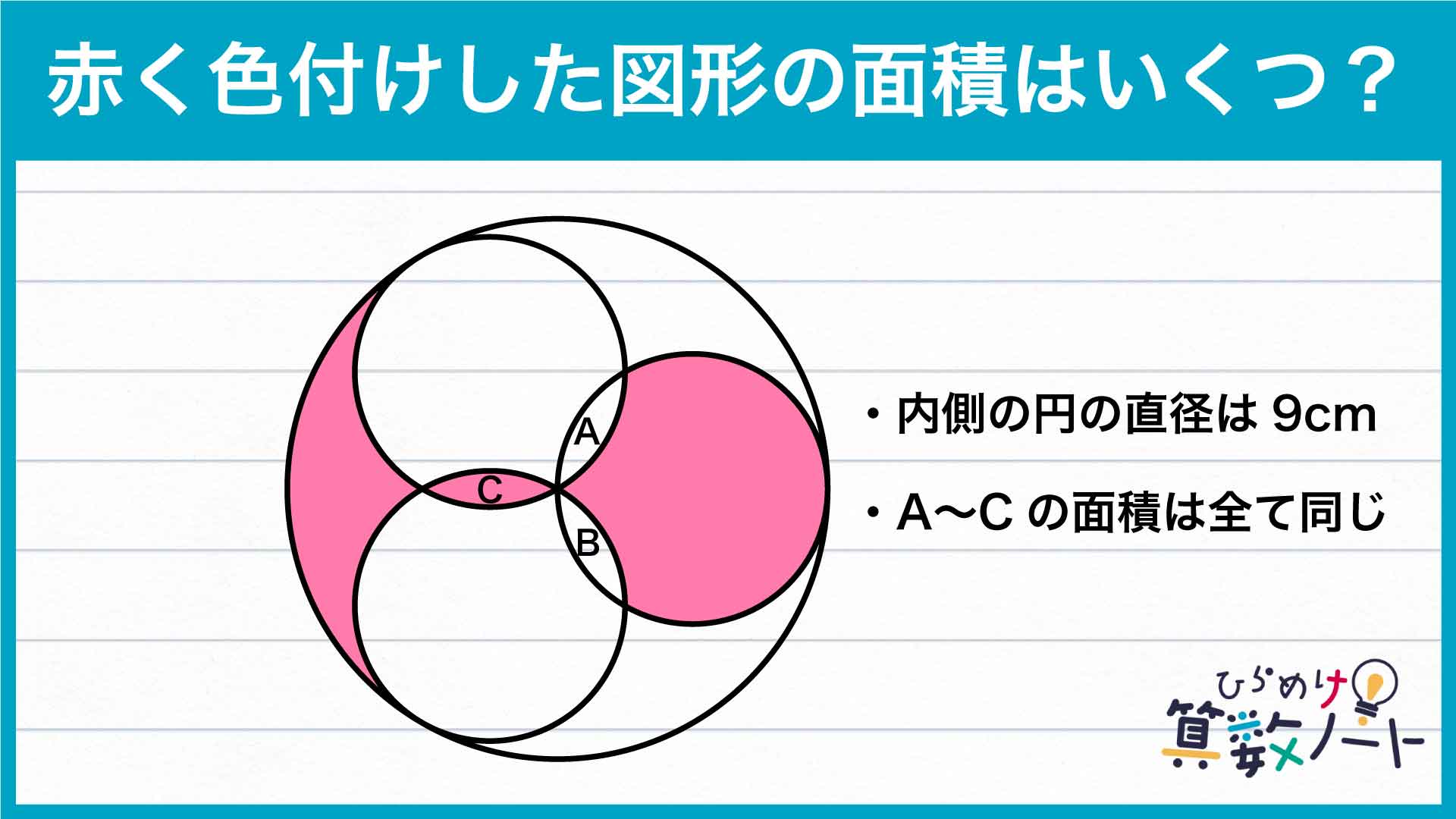
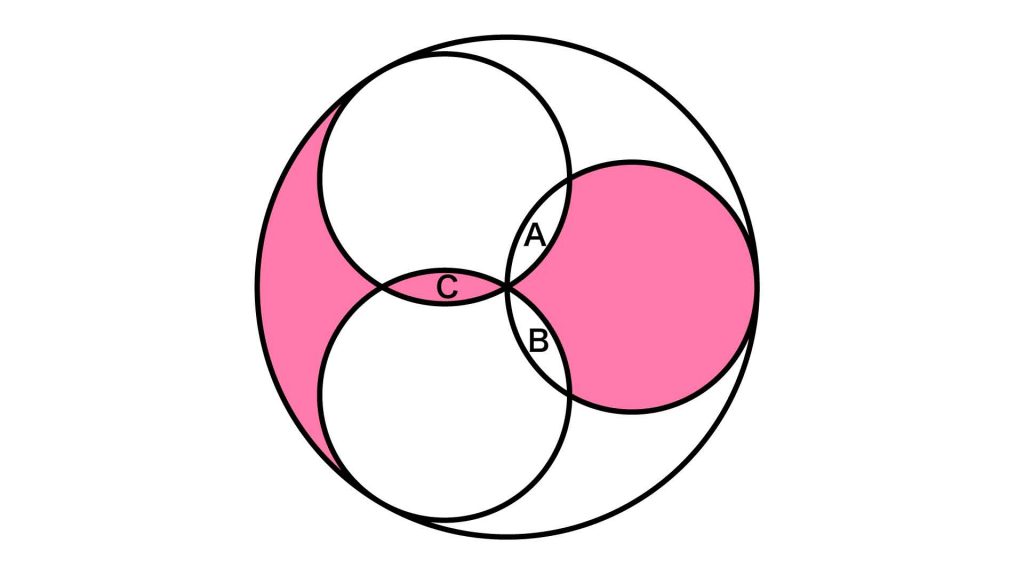
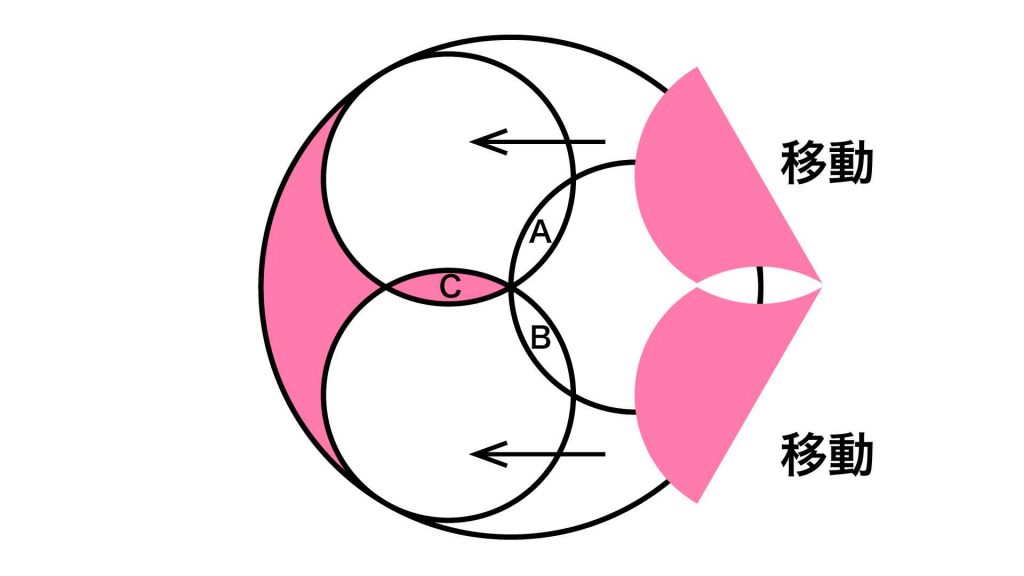
赤色の図形の一部分に注目する
まず、赤色の図形の右側部分の性質を調べます。
この部分は、半径9cmの円から、AとBの図形を2つ引いた図形であることがわかります。
面積を求めやすい図形を作る
ここからは、赤色の図形全体を面積を求めやすい図形に変形していきます。ここで活用するのは、先ほど性質を調べた赤色の図形の右側の部分です。
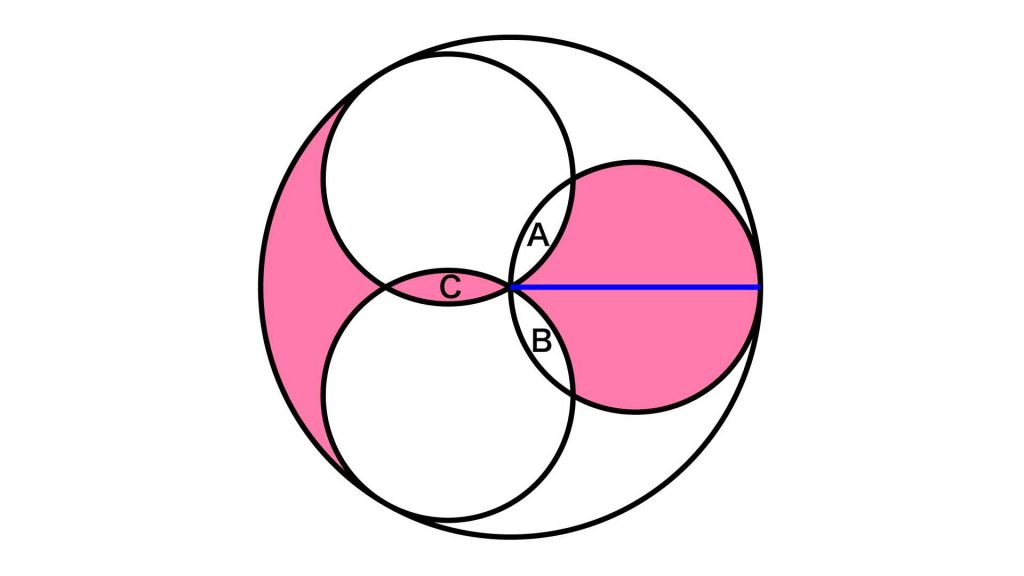
まずは、赤色の図形の右側部分を上下半分に分割します。
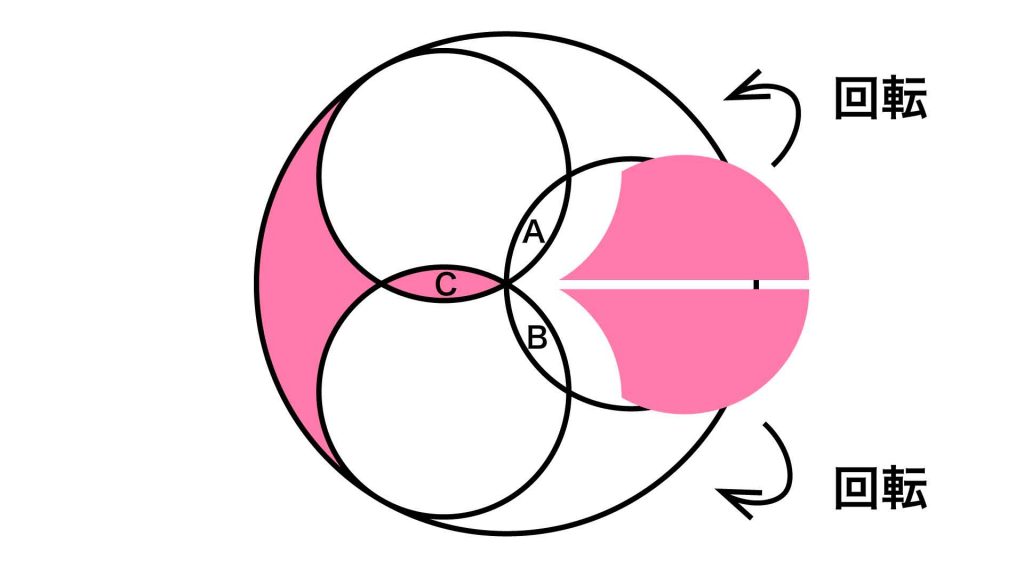
そして、それぞれを図の向きに回転します。
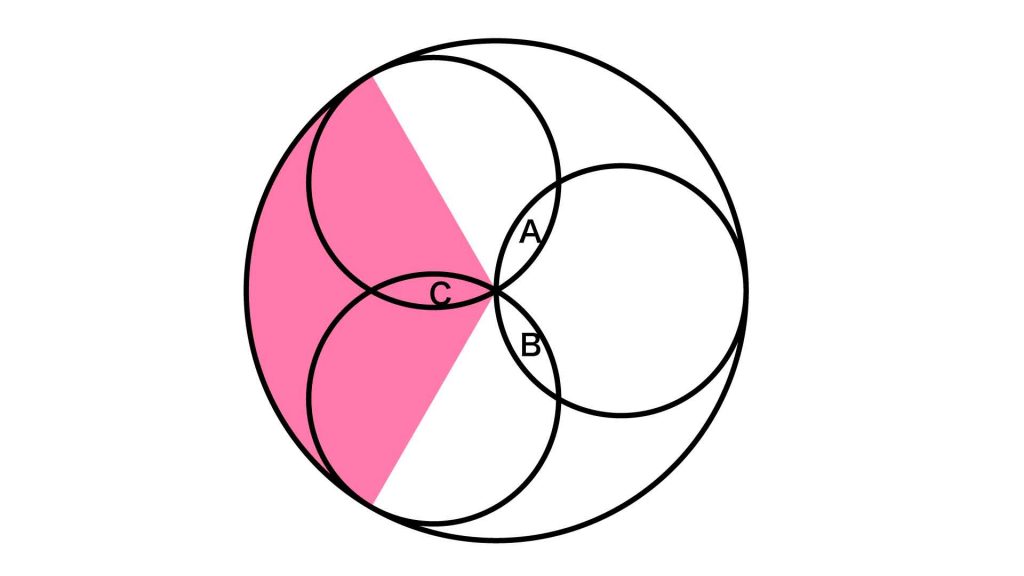
A〜Cはすべて同じ形なので、図形Aの上下に、赤色の図形のくぼんだ部分がぴったりとはまります。
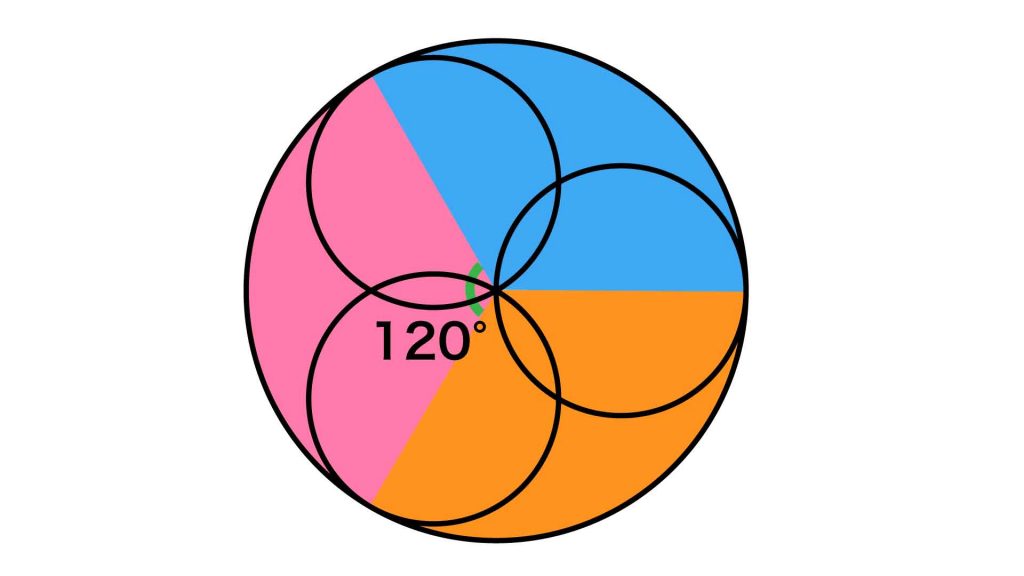
この操作によりできる赤色の扇形の半径は、2つの小さな円の直径と等しいです。小さな円は3つあるので、以下の図のように、赤色の扇形と同じ図形を大きな円の中に3つ作ることができます。
したがって、赤色の扇形の面積は、大きい円の面積の3分の1となります。
大きな円の半径は9cm
大きな円の半径は内側の円の直径に等しいので、9cmです。
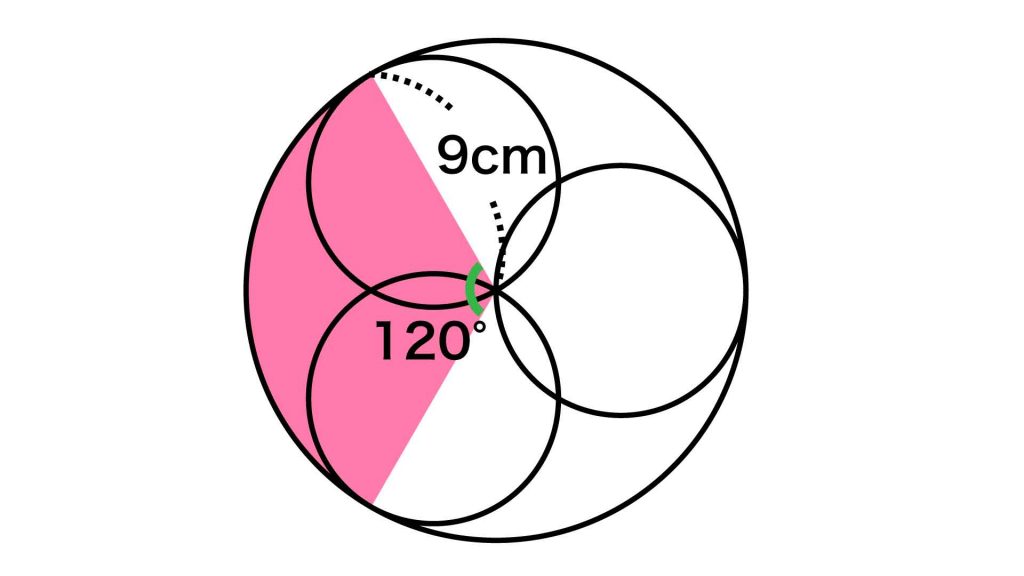
したがって、赤色の図形の面積は、9×9×π÷3=27πcm2となります。
答え:27πcm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










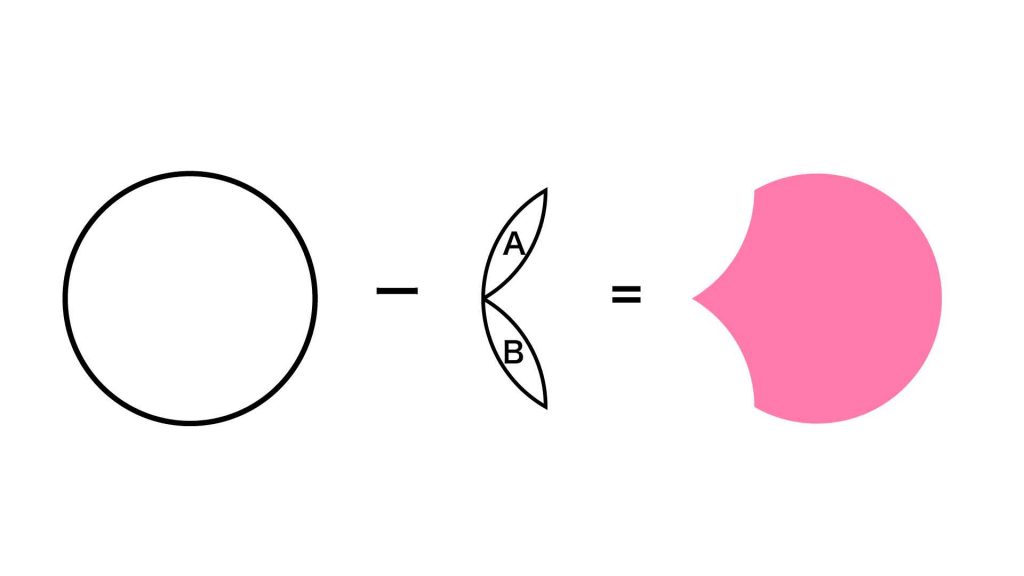
.jpg)








.jpg)