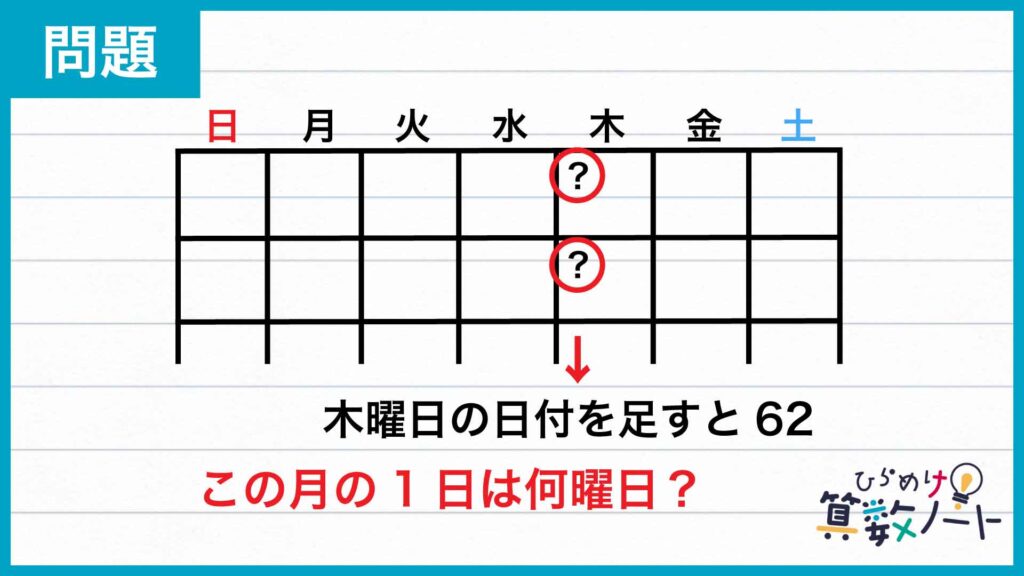
問題はこちら
2ページ:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、
- 日付の数字の和を文字で表す
- 「1日」の曜日を求める
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
日付の数字の和を文字で表す
まず、1カ月のカレンダーの中で最初に訪れる木曜日の日を、文字を用いてd日と表します。そうすると、d日の次に木曜日である日は、ちょうど1週間後である(d+7)日であることがわかります。同じようにして、(d+7)+7=(d+14)日、(d+14)+7=(d+21)日……が木曜日である日の日付になります。
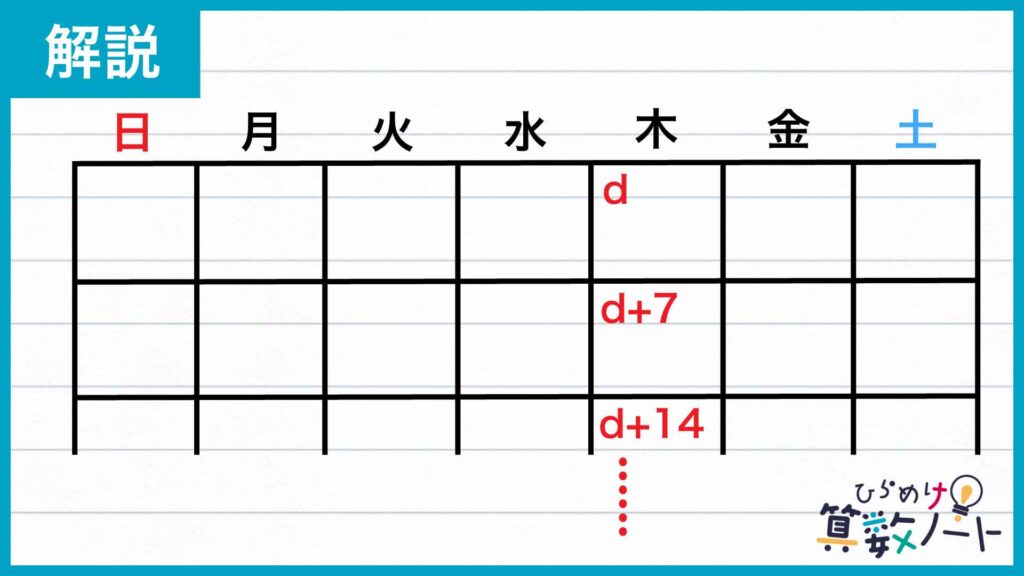
ここで下の図のように、カレンダーに書かれる日付のうち、木曜日であるものは4つか5つです。

1カ月のカレンダーのうち、木曜日である日の日付の和は、文字dを使って「d+(d+7)+(d+14)+(d+21)=4×d+42」または「d+(d+7)+(d+14)+(d+21)+(d+28)=5×d+70」と表せます。
よって、問題文の条件から、4×d+42=62または5×d+70=62が成り立ちます。しかし、5×d+70だと62を越えてしまいますので、4×d+42=62が成り立つことがわかります。
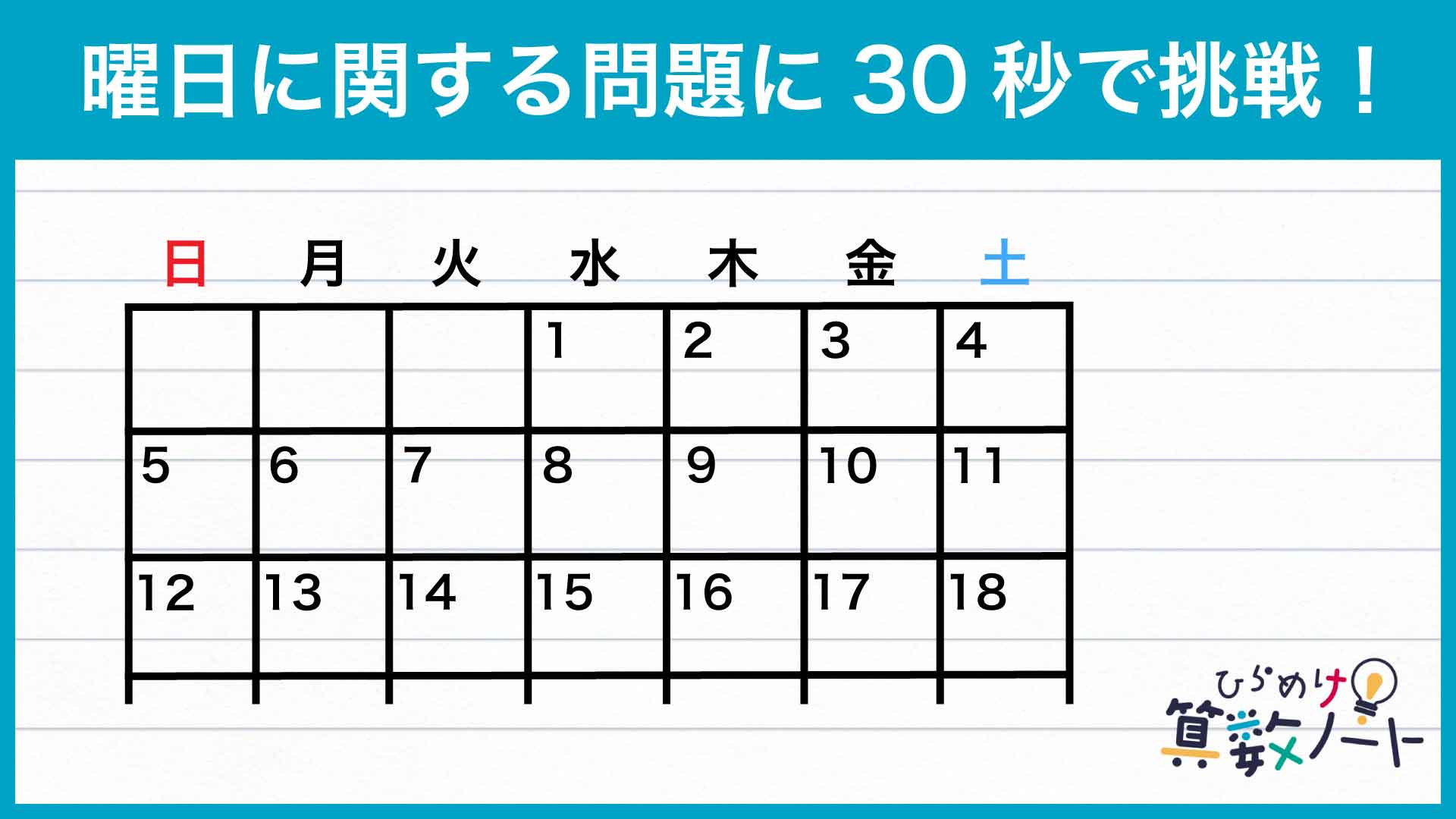
4×d+42=62より、d=5が判明。したがって、1カ月のカレンダーの中で最初に訪れる木曜日の日付は5日ということがわかります。
「1日」の曜日を求める
ここまで来ると、あとはもう一息です。
1カ月のカレンダーの中で最初に訪れる木曜日が「5日」であることから、同じ月の「1日」の曜日は、木曜日から数えて4日前の曜日です。

したがって、求める曜日は、木曜日の4日前である「日曜日」になります。
答え:日曜日
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】








.jpg)









.jpg)






