小学生でも解ける「正十四角形」の問題。あなたは解ける？

【問題はこちら】

1ページ目：自力で解きたい方はこちらへ！以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題の解き方をまとめた図がこちらになります。

ポイントは、①と②の面積を別々に求めるのではなく、2つの図形をまとめて考えることです。これを踏まえて解いていきましょう！

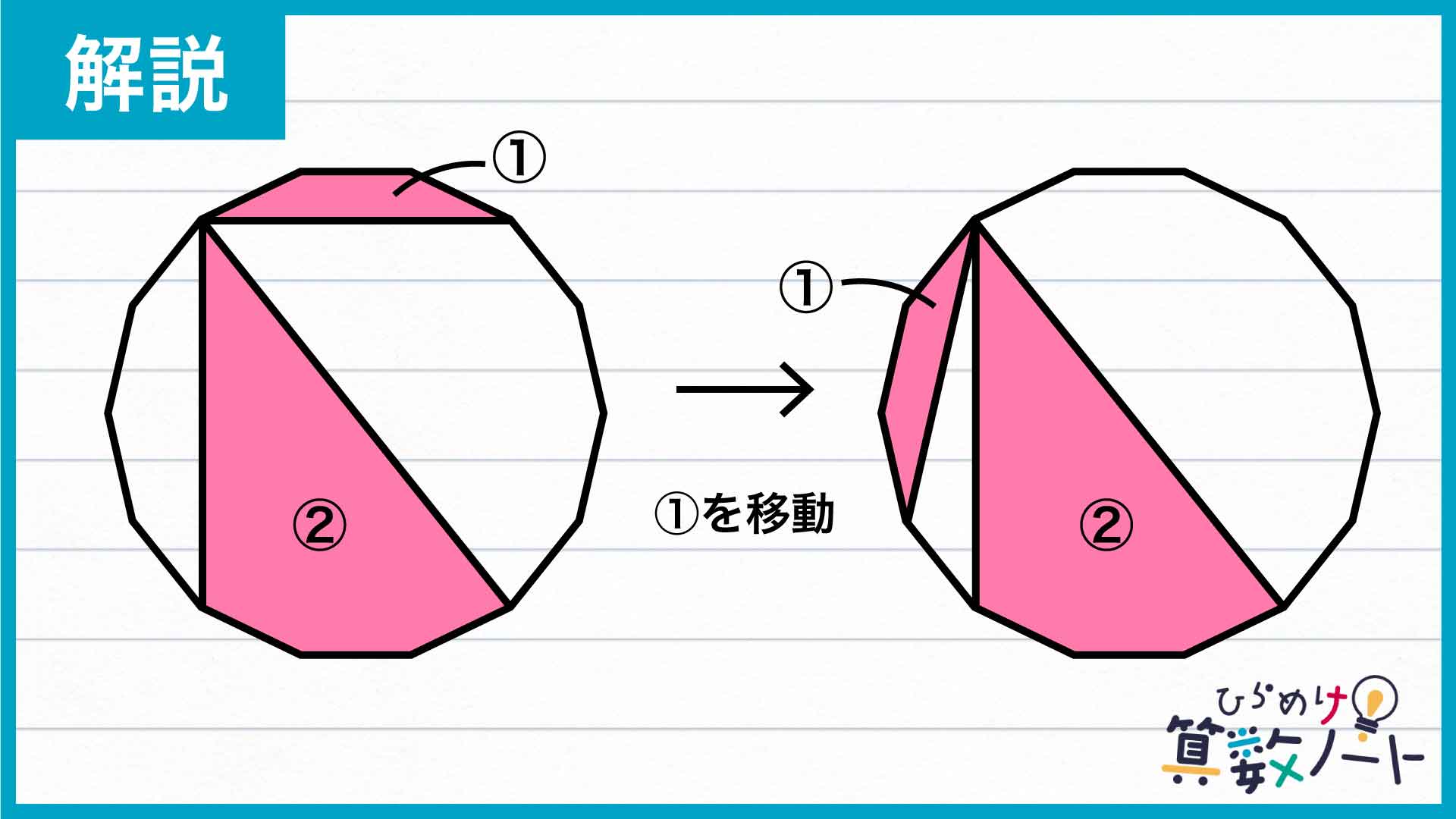
赤い図形を移動させる

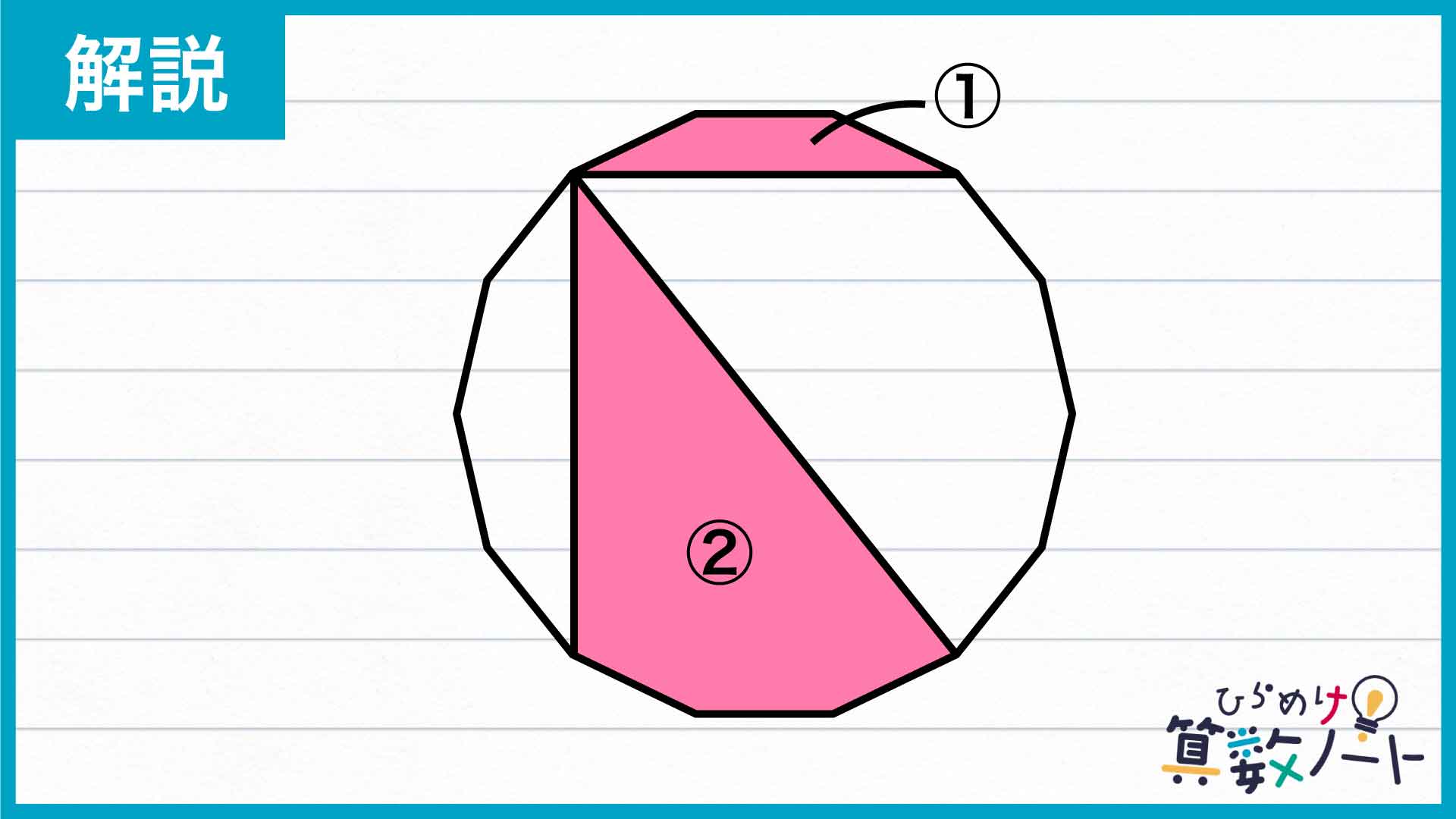
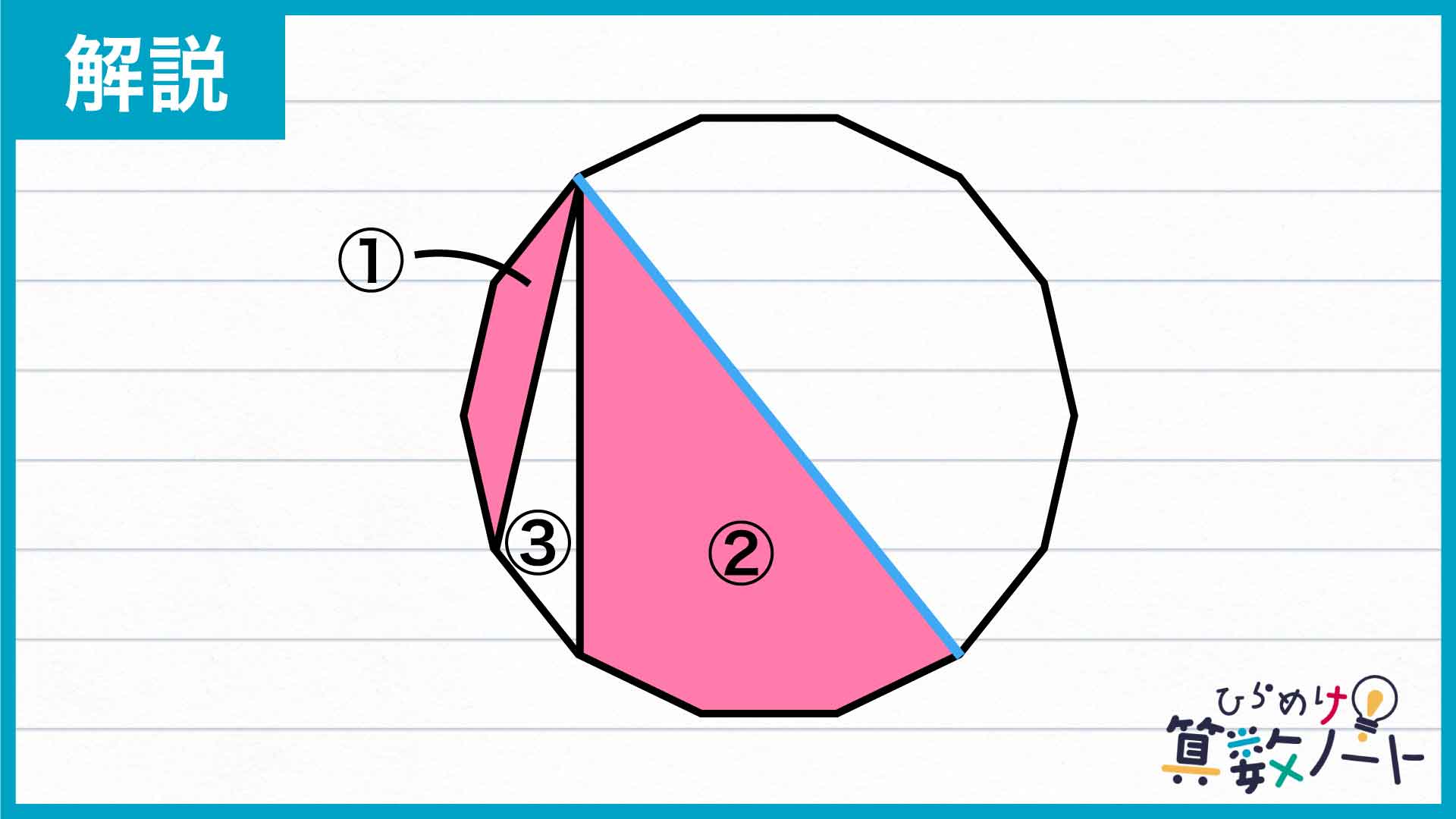
下の図のように、赤く色をつけた図形にそれぞれ①、②と振ります。

すると①は、正十四角形の隣り合う3つの辺と、その両端の頂点を結ぶ線分に囲まれた図形なので、図のように移動させても面積は同じです。

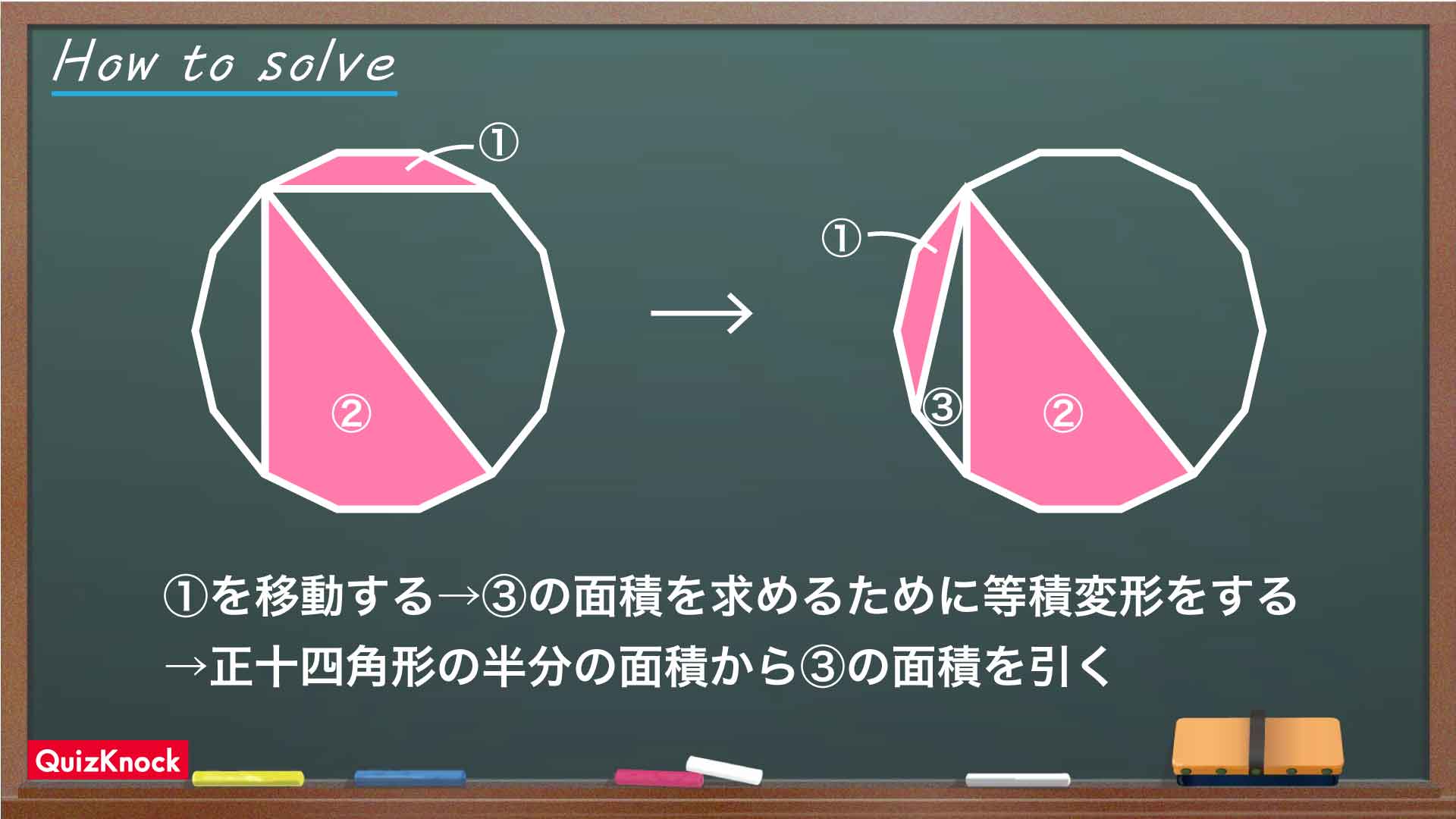
このとき、①と②に挟まれた部分を③とすると、下の図の青い対角線は正十四角形の中心を通るため、①、②、③の面積の合計は、正十四角形の半分の70cm²であることがわかります。

③の面積を求める

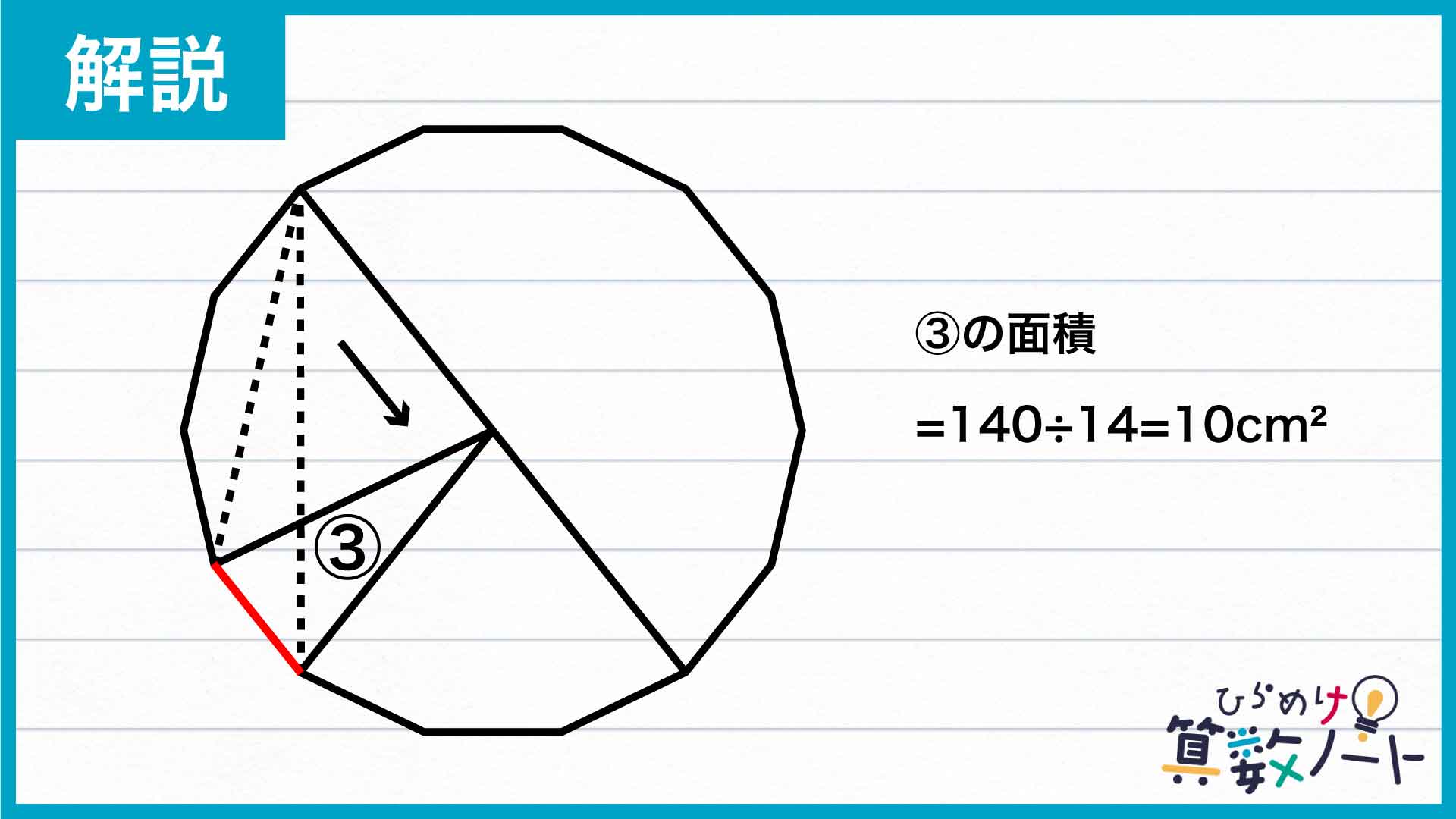
③の三角形について、下の図の赤い辺を底辺と見ると、この辺は正十四角形の中心を通る対角線と平行なので、残りの頂点を正十四角形の中心に移動しても高さが変わらず、したがって面積も変わりません。

したがって、③は正十四角形を14等分した図形であることがわかるので、③の面積は140cm²÷14=10cm²です。

①と②の面積の合計を求める

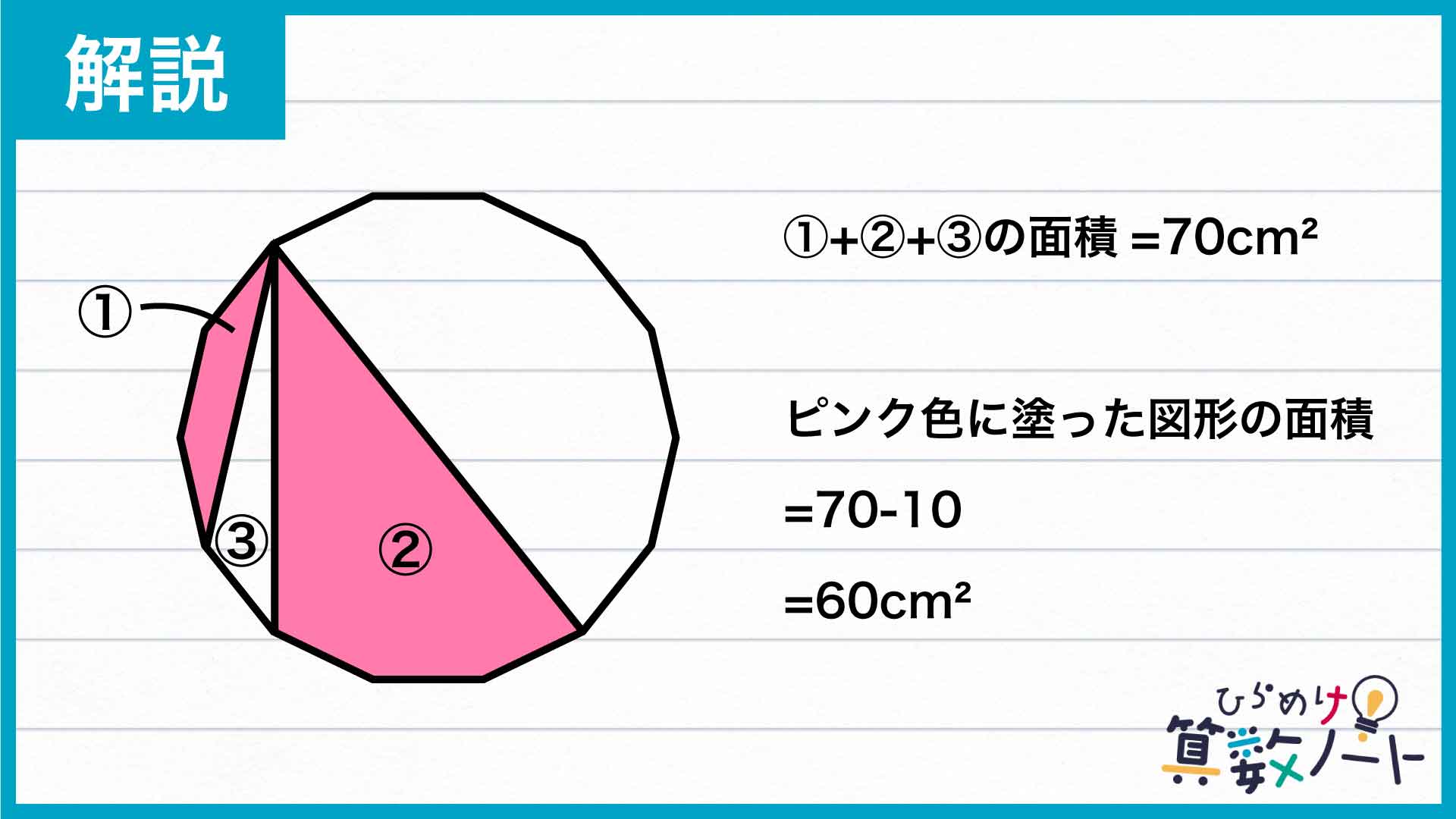
ここまで来ればあとは簡単です。先ほど説明した通り、①、②、③の面積の合計は、正十四角形の半分の70cm²なので、①、②の面積の合計、すなわち赤く色付けした部分の面積の合計は70-10=60cm²です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】