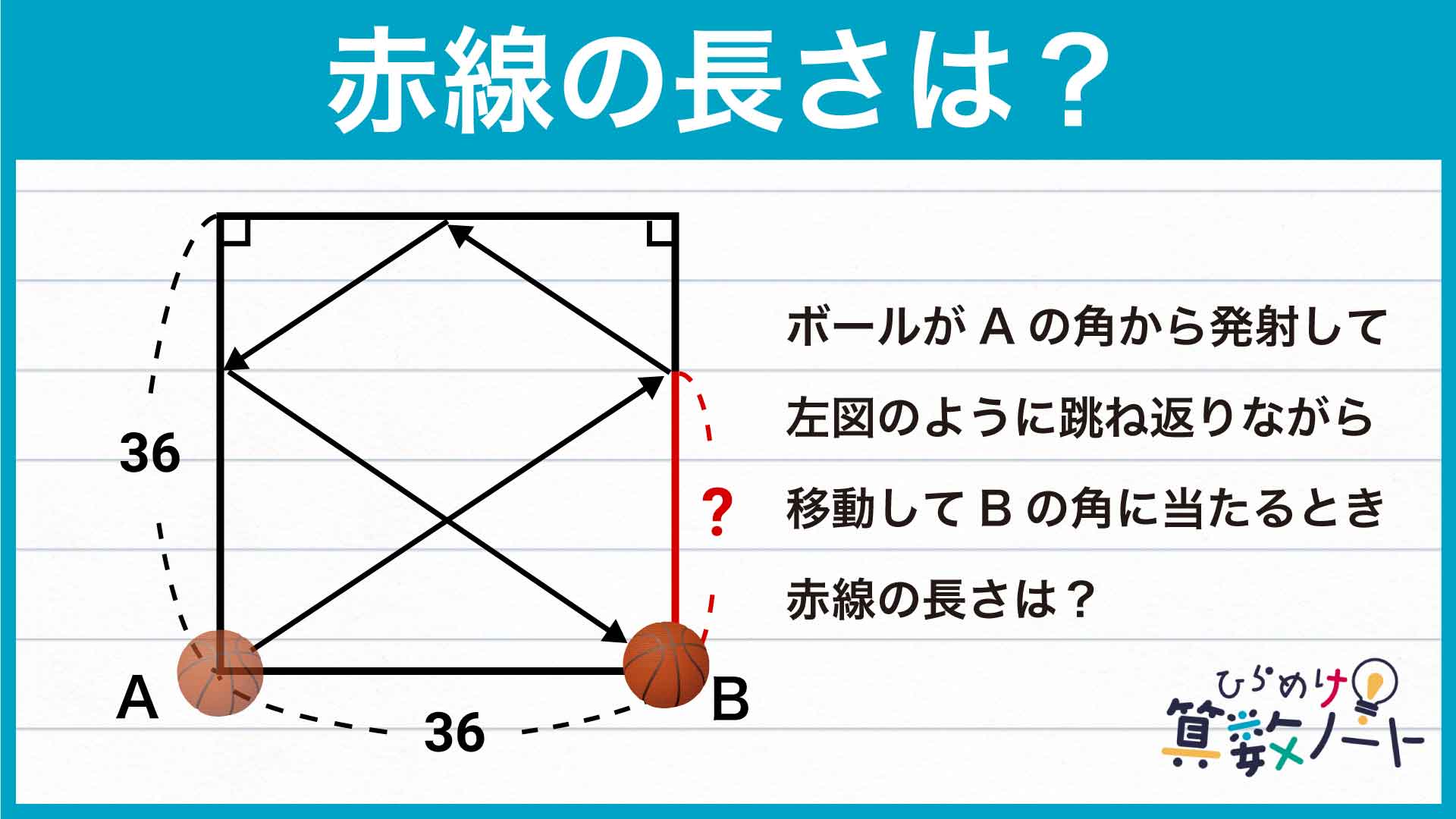
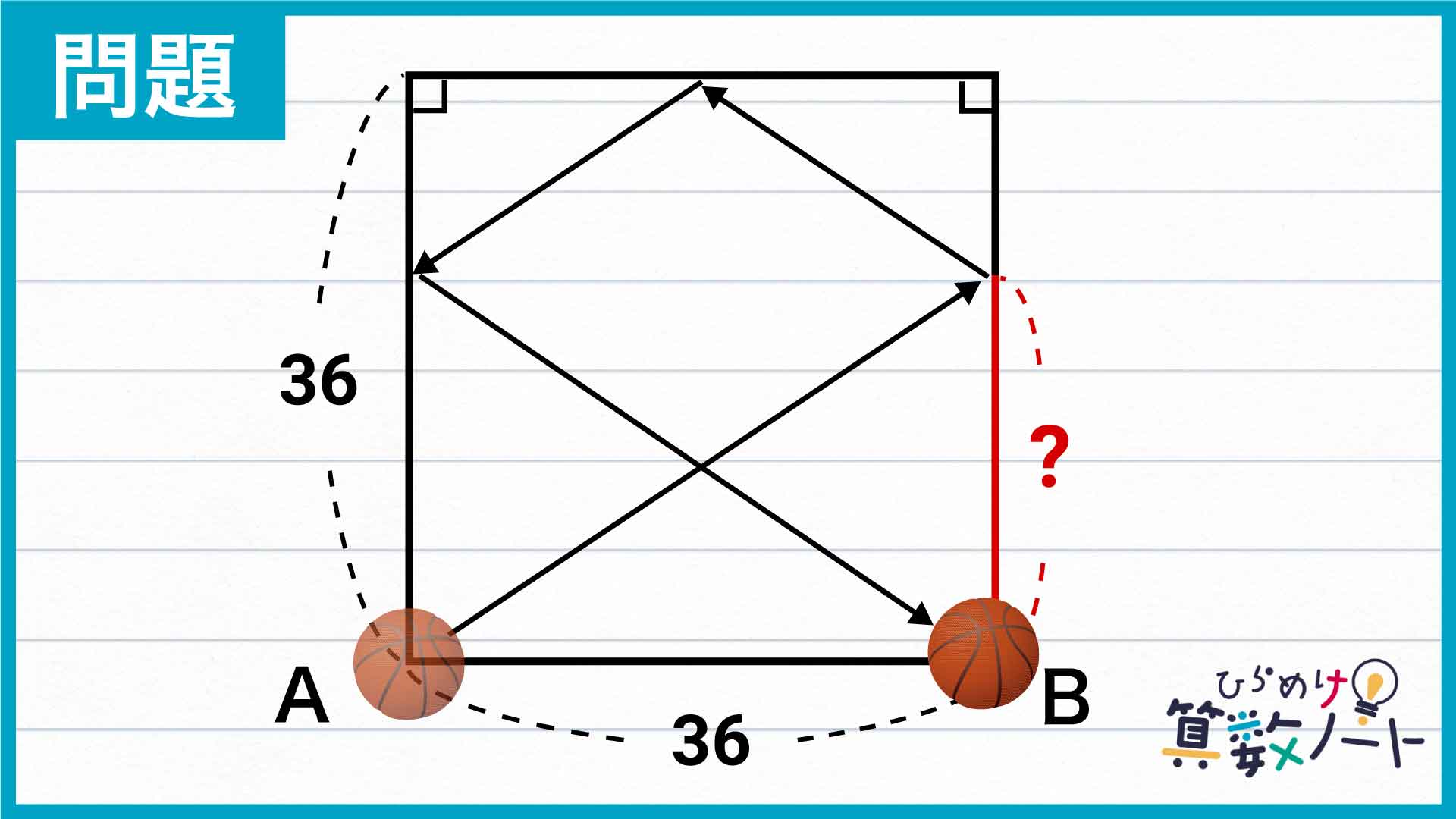
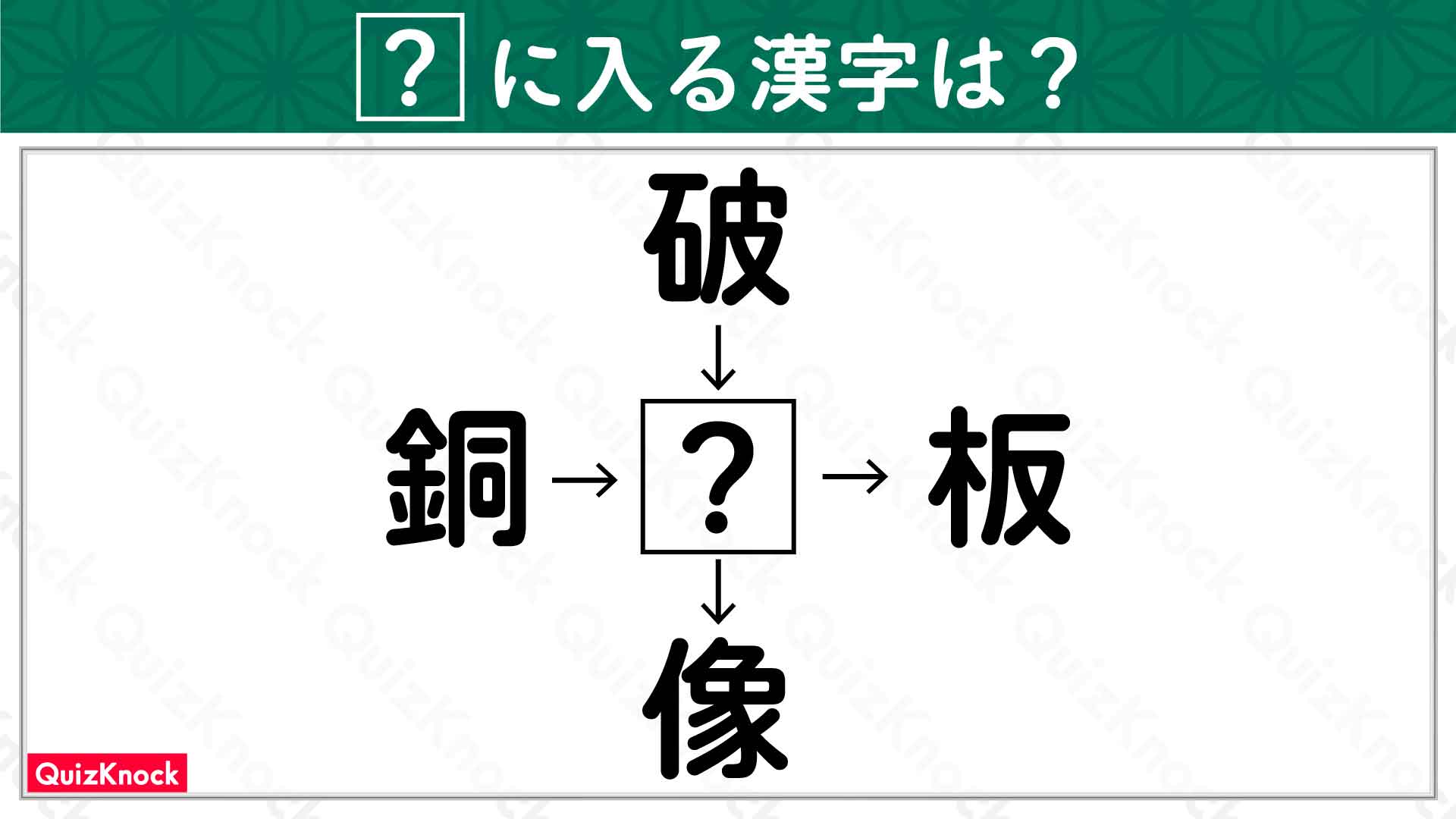
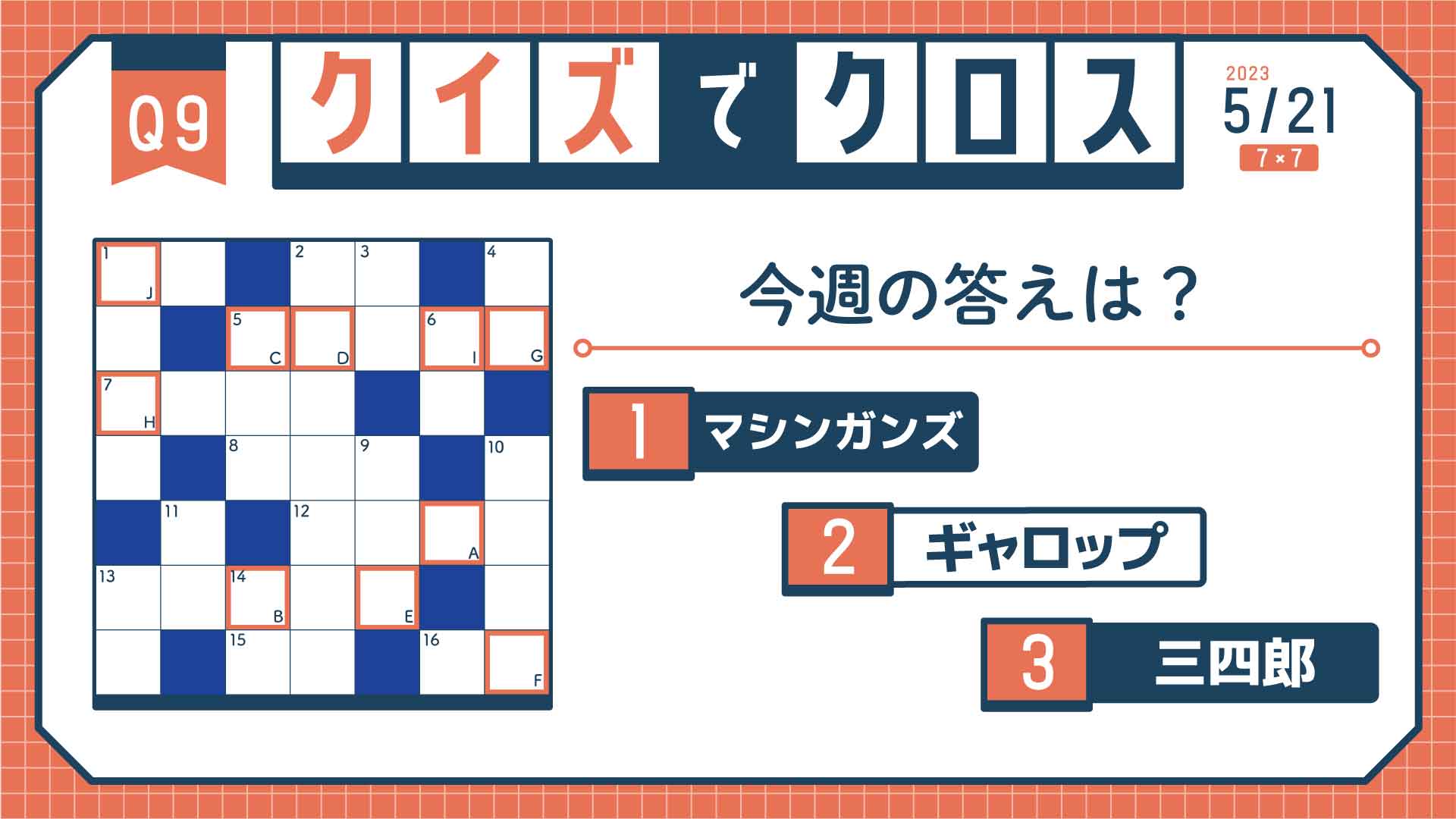
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
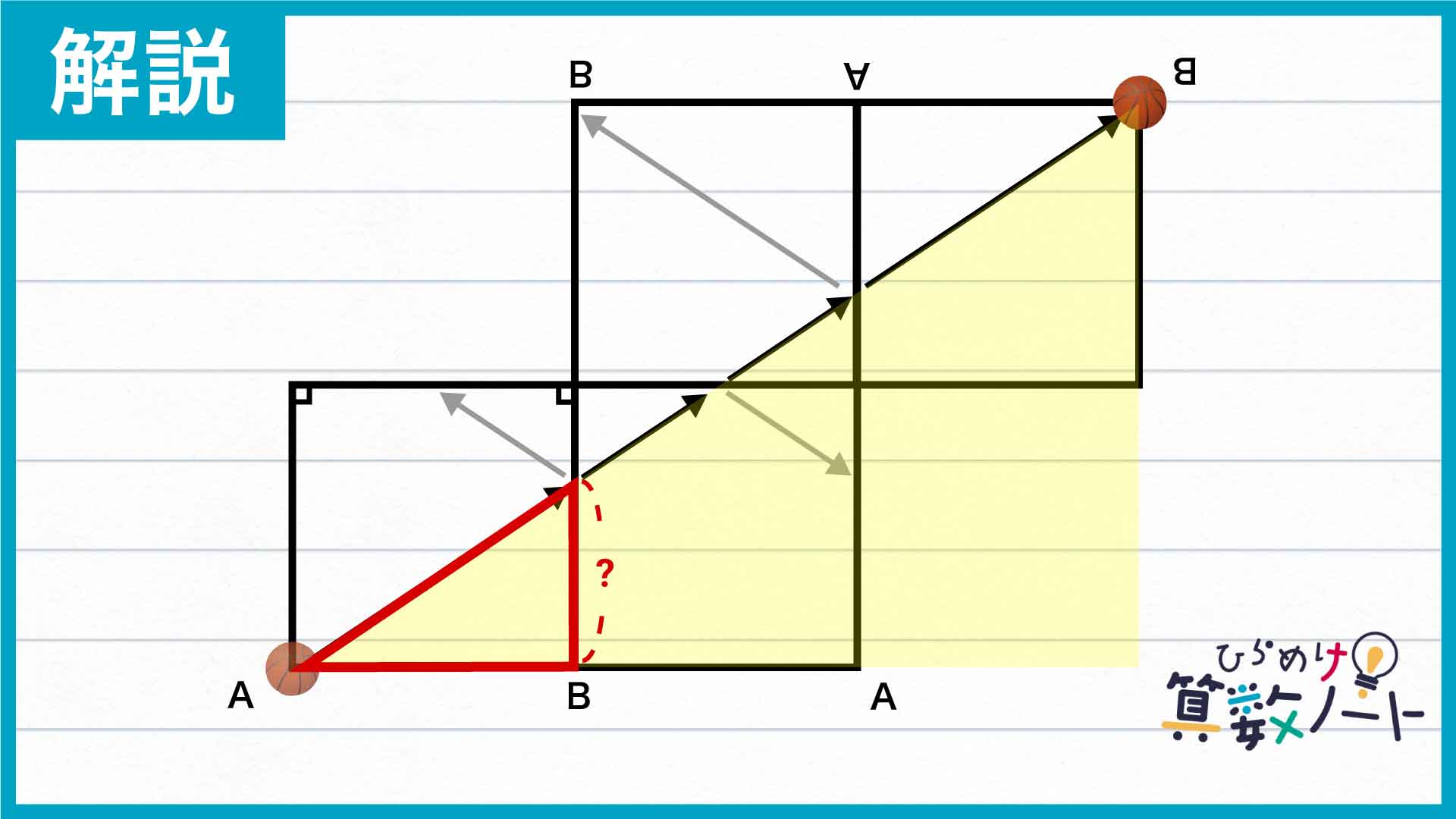
この問題の解き方をまとめた図がこちらです。
ポイントは、ボールがはね返る壁の方向に部屋をつなげていき、ボールの通った道筋を一本の直線として考えることです。
では、このポイントを踏まえつつ解いていきましょう!
「新しい部屋」を付け足す
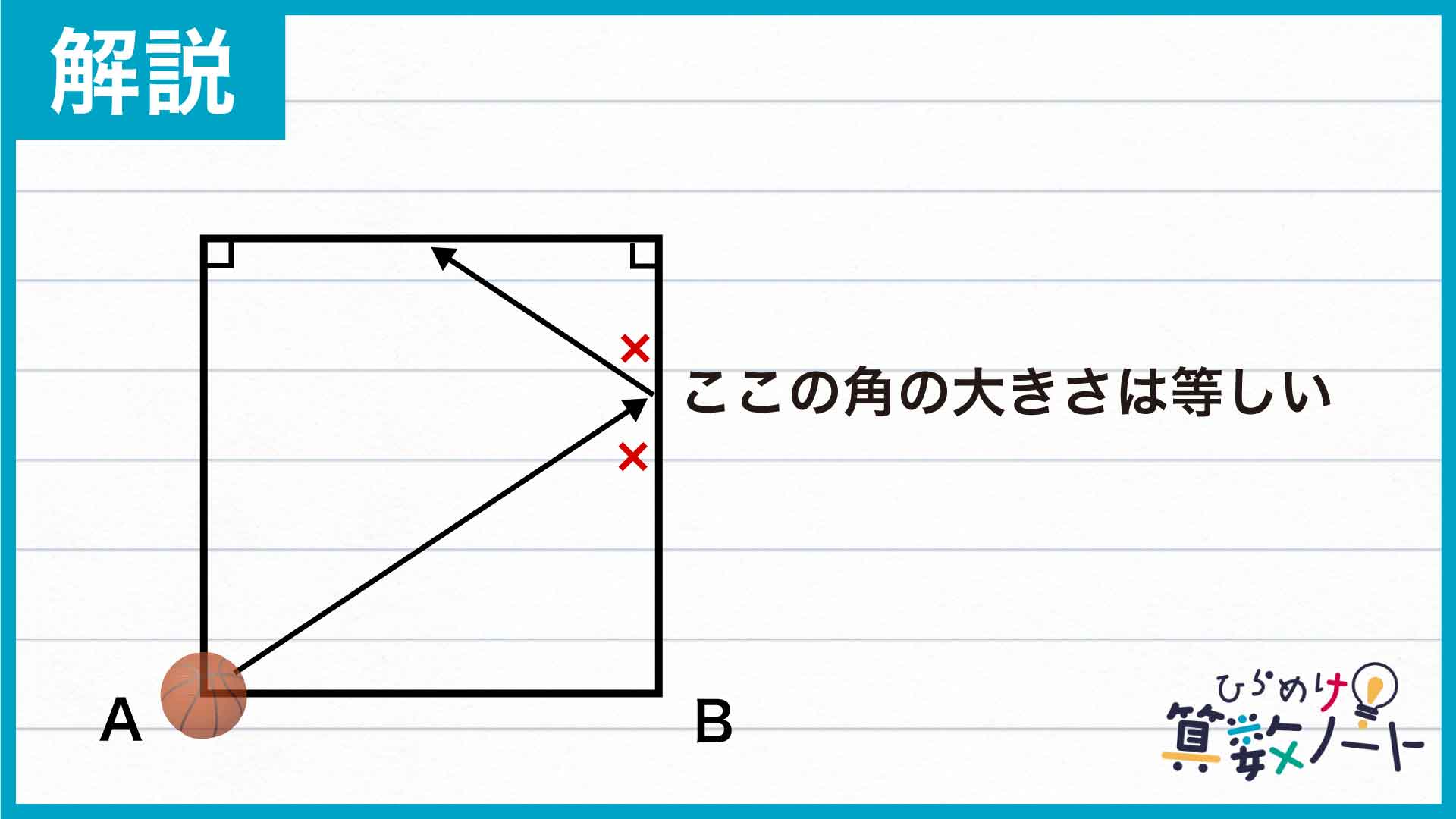
まず、1回目のはね返りについて考えます。問題に与えられた条件より、ボールが壁に当たってはね返るとき、下の図に×で示した角は互いに大きさが等しくなります。
このはね返りについて考えやすくするために、この部屋を左右反転させ、ボールが当たった壁の側にくっつけてみましょう。はね返ったあとの道筋を示す矢印も一緒に反転させると、やはり同じ大きさの角×が現れます。
上の図で赤く示された2つの角×は、大きさが等しいことから対頂角の関係にあるとわかります。したがって反転させたあとの矢印はボールがはね返る前の道筋を示す矢印と一直線の関係にあり、まるでボールが壁を突き破ってまっすぐ隣に行ったかのような図ができるのです。
部屋をどんどんつなげて考える
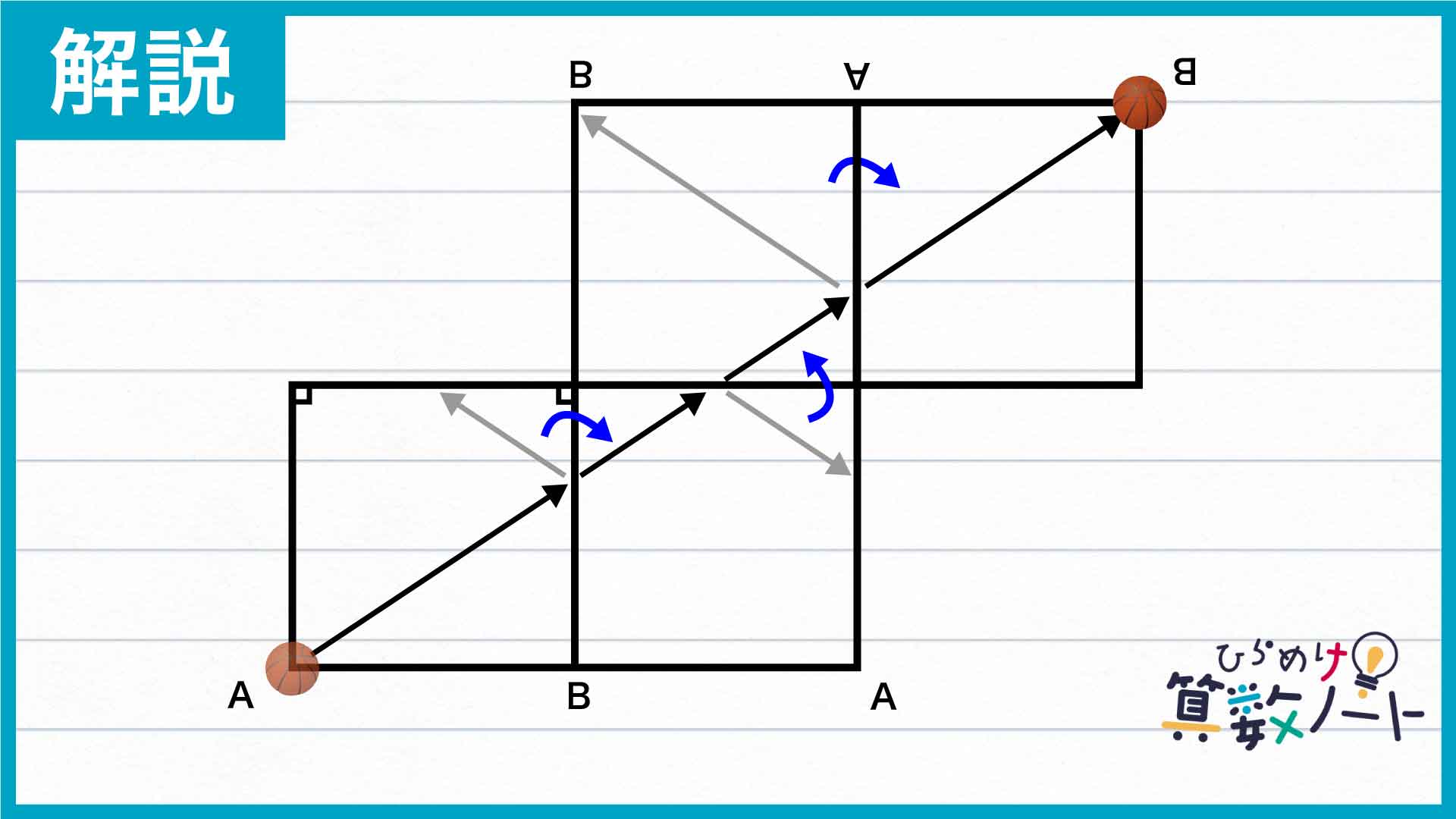
2回目以降のはね返りについても、考え方は同じです。ボールが当たった壁を軸として、反転させた部屋を一つずつつなげていきます。
一つの部屋の中で折れ曲がっていたボールの道筋を、左下の角Aから右上の角Bに向かって伸びる一直線の道筋として図示し直すことができました。ここで、下の図に示された黄色の大きい直角三角形と、赤色の小さい直角三角形に注目してみましょう。
2つの直角三角形は、直角以外の1つの角が共通していることから相似の関係にあります。底辺の長さに注目してみると、それぞれ正方形の1辺と1辺×3の長さに等しいことから、相似比は1:3であるとわかります。正方形の1辺の長さは36なので、高さの比より求める長さは36×2÷3=24であるとわかるのです。
答え:24
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】