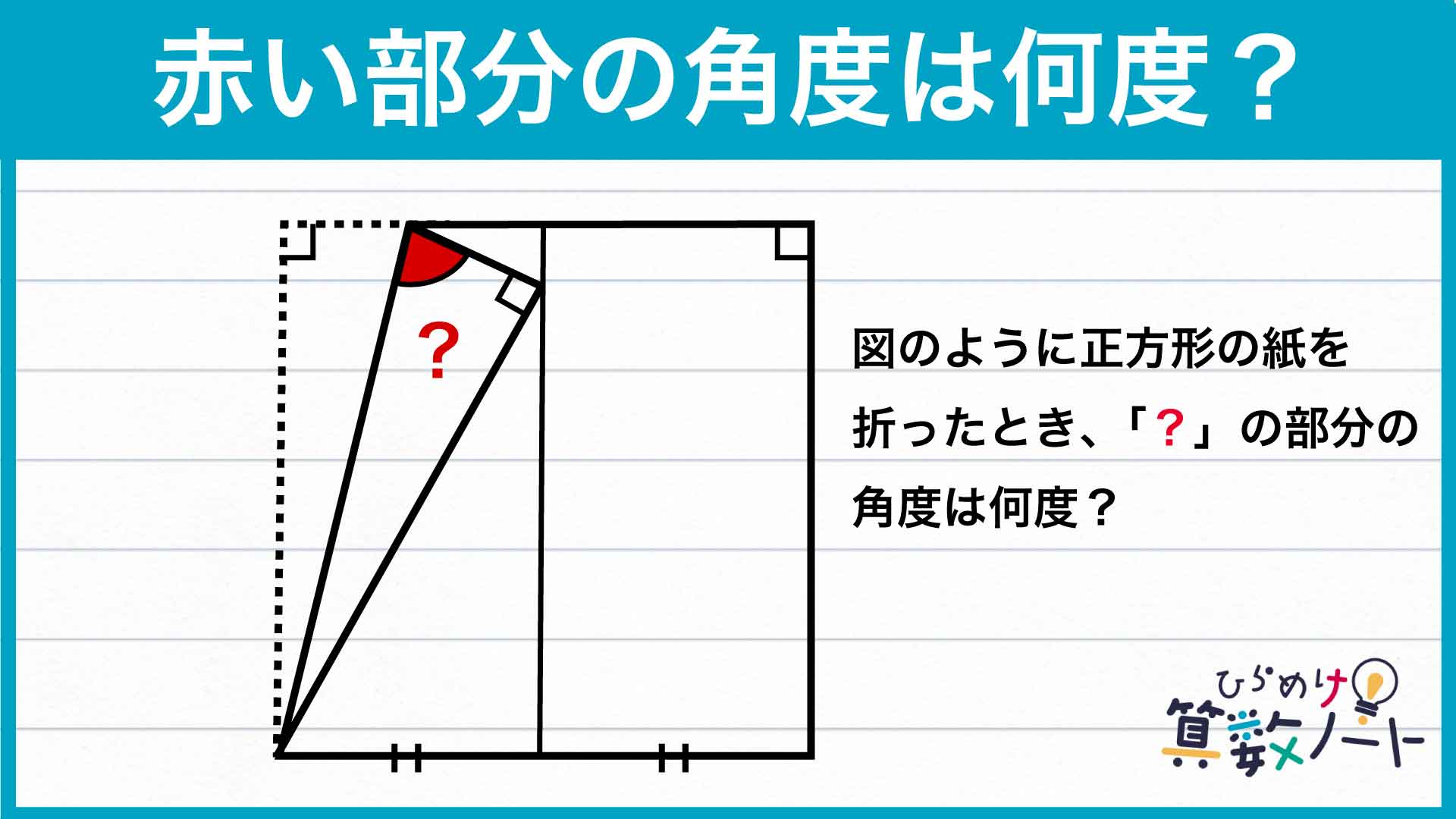
【問題はこちら】
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
【解説】
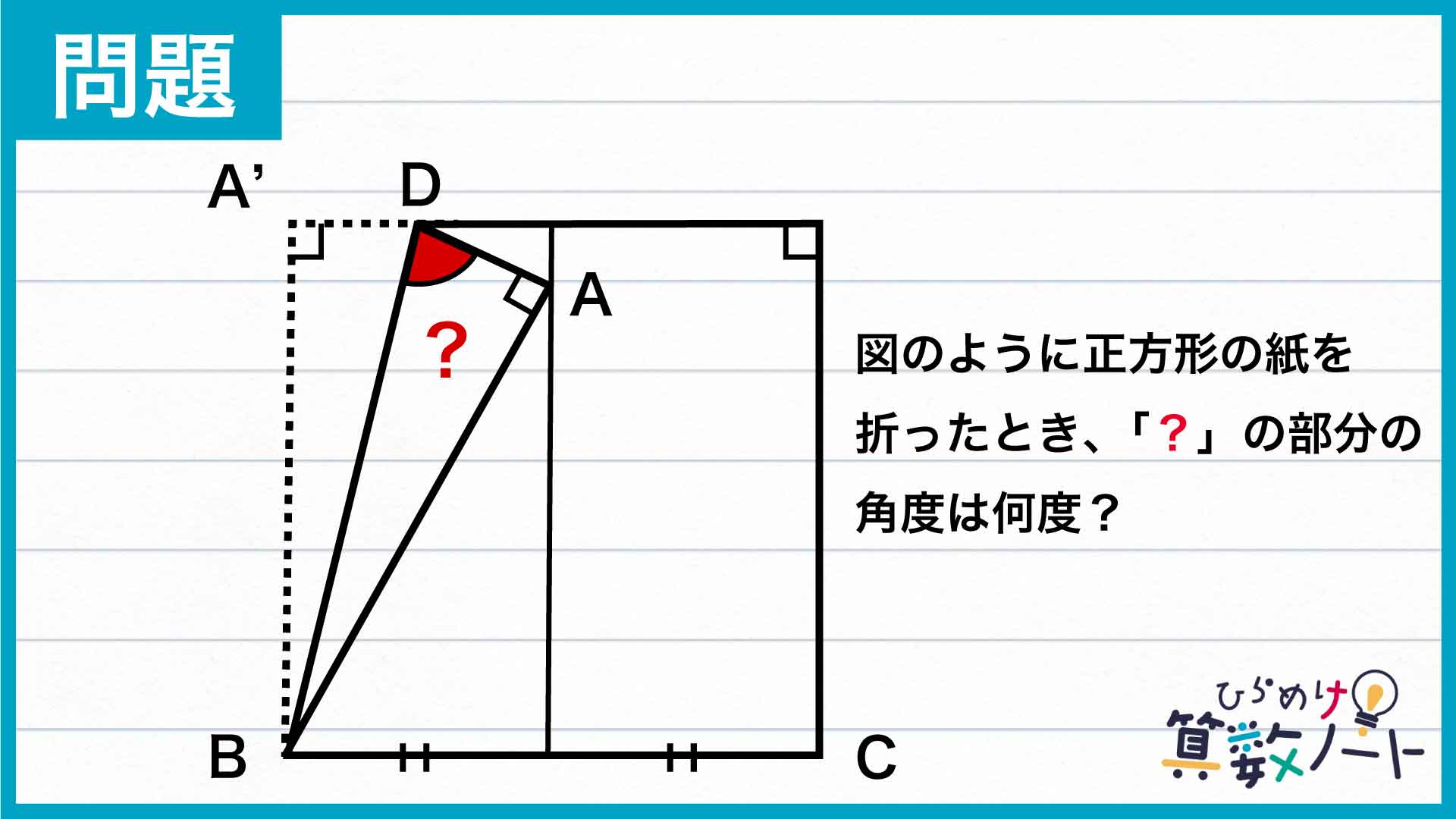
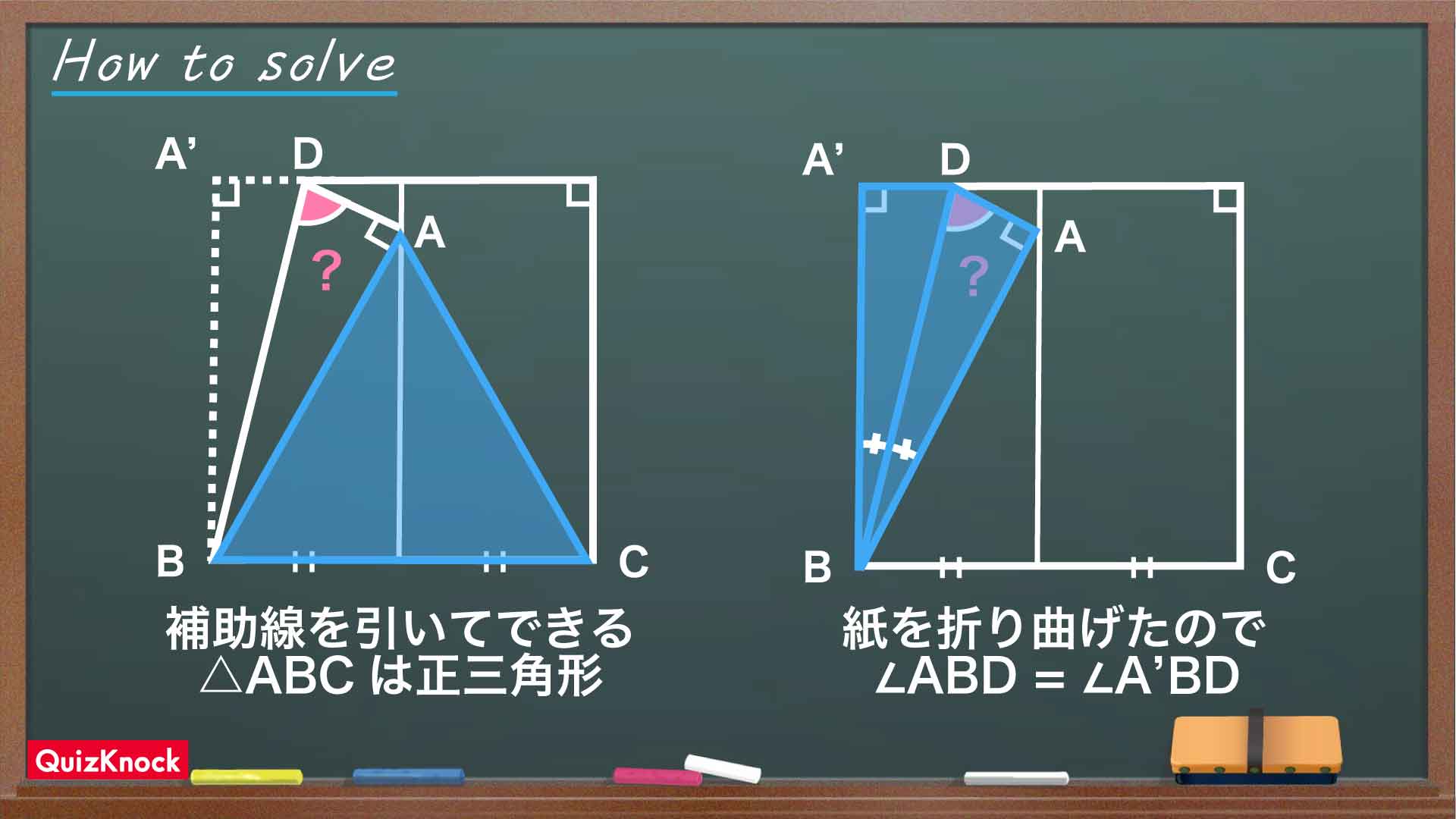
今回の解き方をまとめた図がこちらです。補助線を引き、頂点Aを含む三角形に注目して、角度をひとつひとつ求めていくことがポイントです。
では、このポイントを踏まえて解いていきましょう!
補助線を引くと、三角形ABCが現れる
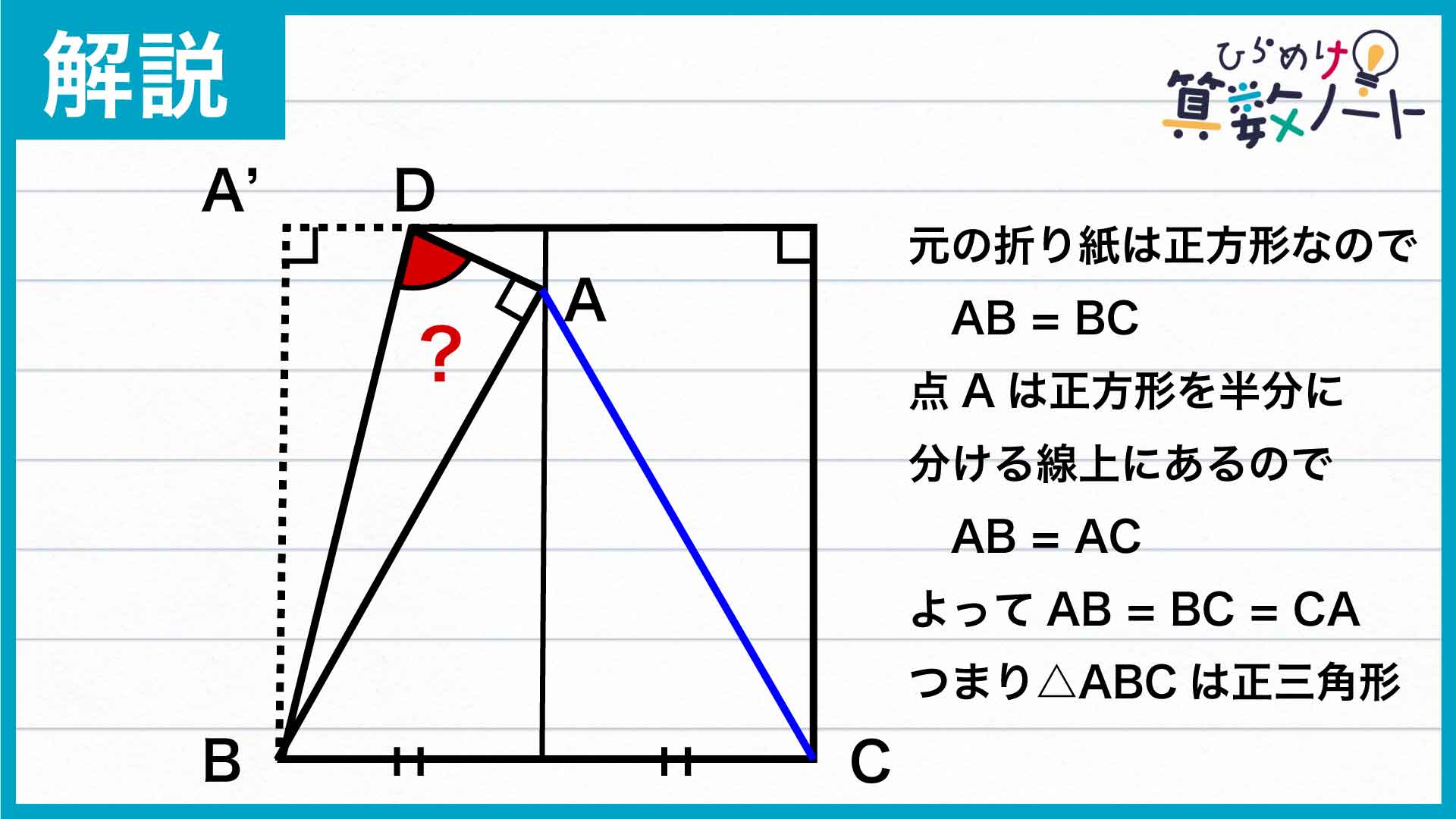
まずは、下の図のように補助線を引きましょう。新しくできた三角形ABCはどんな図形でしょうか。
辺AB、辺BCはともに正方形でできた折り紙の一辺なので、辺ABと辺BCの長さは等しいことがわかります。また、点Aは正方形を半分に分ける線上にあるので、辺ABと辺ACの長さも等しいことがわかります。従って、三角形ABCはすべての辺の長さが等しく、正三角形とわかります。
正三角形からわかること
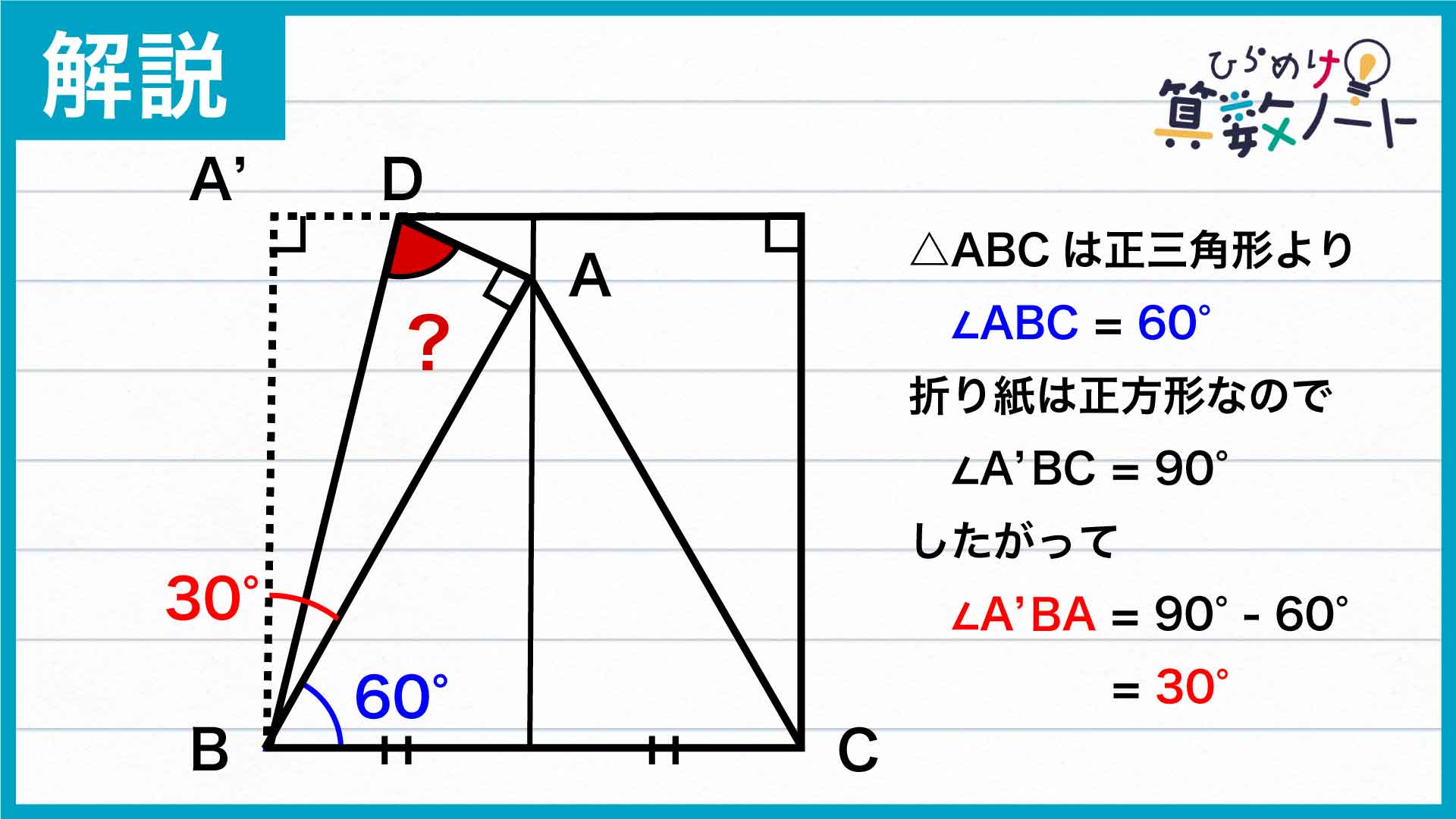
三角形ABCが正三角形とわかったので、角ABCの大きさは60度となります。
さらに、折り紙は正方形なので、角A'BCの大きさは90度です。つまり、角A'BAの大きさは30度とわかります。
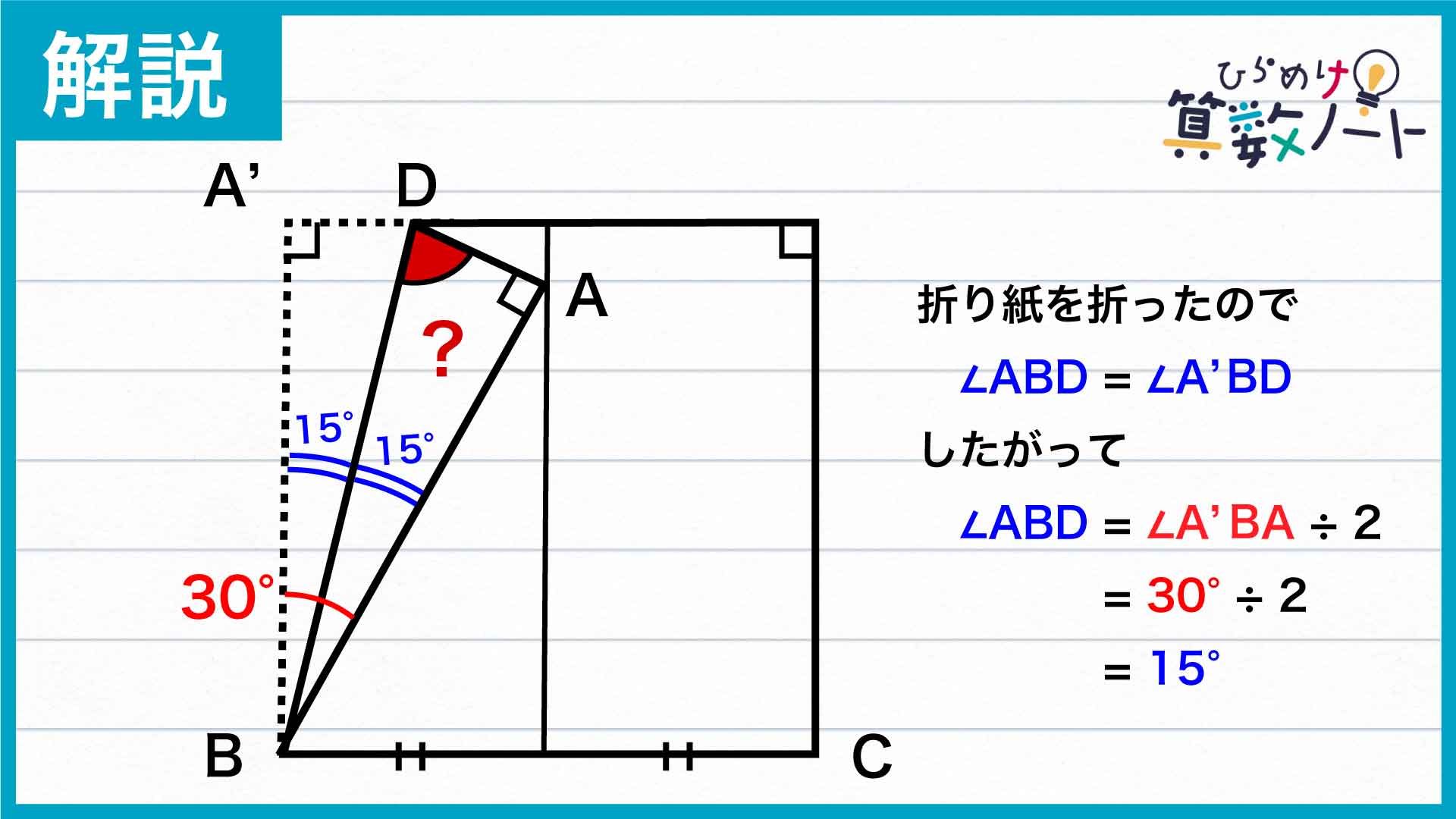
折り紙の性質を活用して、角ABDの大きさを求める
次に、角A'BDと角ABDに着目します。折り紙を折りたたんでいることから、これらの角は大きさが等しいですね。よって、角ABDの大きさは、角A'BAの半分である15度とわかります。
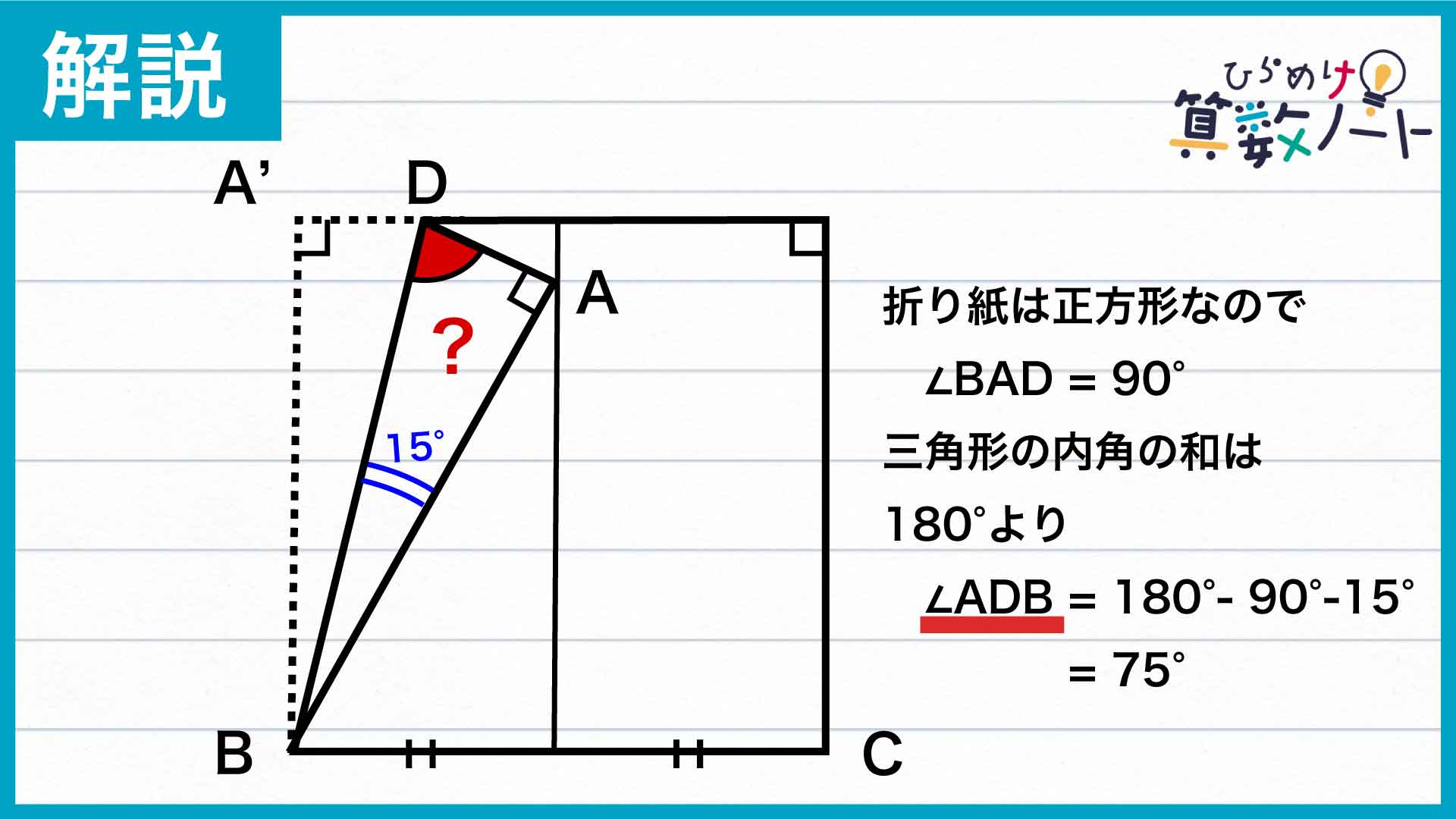
最後は三角形DBAに着目!
最後に、三角形DBAの3つの内角を考えましょう。いま、角ABDの大きさは15度と求まりました。さらに、点Aはもともと正方形の頂点だったので、角BADの大きさは90度です。
三角形の内角の和は180度なので、求めたい角ADBの大きさは、180度からこれら2つの角の大きさを引くことで求めることができます。したがって、角ADBの大きさは、180-90-15=75度です。
答え:75度
以前出題した、こちらの類題にもぜひチャレンジしてみてくださいね。それでは、また次の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)